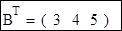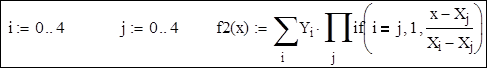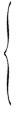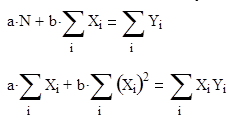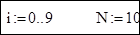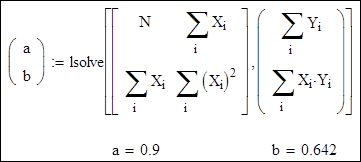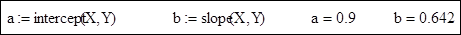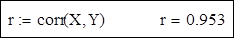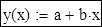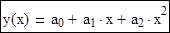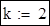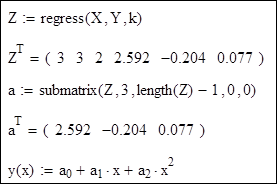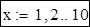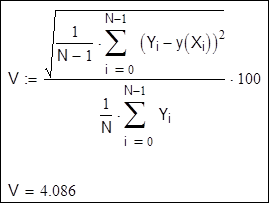Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Збереження файлів, друк і вихід з MathcadСодержание книги
Поиск на нашем сайте
ВСТУП
Методичні вказівки містять стислі відомості про популярну систему комп'ютерної математики Mathcad, яка бурхливо розвивається. Розглянуто інтерфейс системи, технологія розв'язання різних задач і візуалізація результатів. Надані завдання і зразки виконання лабораторних робіт з необхідними зауваженнями, коментарями, таблицями і рисунки з різних розділів математики – від матричної алгебри до розв'язання диференціальних рівнянь і апроксимації. Методичні вказівки призначені для студентів і аспірантів, що займаються вивченням математичних методів і застосуванням систем комп'ютерної математики для розв'язання науково-технічних і інженерних задач. Одна з задач ПЕОМ – автоматизація інтелектуальної праці, підвищення ефективності наукових досліджень. З цією метою розробляються математичні пакети прикладних програм, які розраховані на широкі кола фахівців. До подібних пакетів належать Mathcad, Mathematica, MatLab+Simulink, Maple, Eureka, Gauss та ін. Mathcad – універсальний математичний пакет, призначений для виконання інженерних і наукових розрахунків. Основна перевага пакета – загальноприйнята математична мова, на якій формулюються розв'язувані задачі. Об'єднання текстового редактора з можливістю використання загальноприйнятої математичної мови дозволяє користувачеві одержати готовий підсумковий документ. Пакет має широкі графічні можливості, розширювані від версії до версії. До достоїнств Mathcad можна віднести: – простота у використанні і легкість у навчанні. Більшість дій, необхідних для управління програмою, є інтуїтивно прозорими, і на освоєння її можливостей людині, що працювала раніше в середовищі Windows, потрібно небагато часу; – можливість виконання обчислень високого ступеня складності. Крім звичних чисельних розрахунків система здатна робити символьні перетворення, наприклад:
– широкі графічні можливості. Велика кількість типів графіків полегшують візуалізацію даних; – інтеграція з Internet, що дозволяє використовувати фрагменти розрахунків, збережені в надрах його безмережних інформаційних ресурсів; – підтримка технології OLE; – наявність текстового редактора, що підтримує інтерфейс WYSIWYG. Це дозволяє готувати звіти, статті і технічну документацію прийнятної якості, не виходячи з Mathcad. РОБОТА В СЕРЕДОВИЩІ Mathcad Для запуску Mathcad необхідне подвійне клацання по піктограмі Mathcad, він викликає появу заставки. Потім відкривається вікно застосування.
Пакет Mathcad – повноцінне Wіndоws-застосування, тому правила і прийоми роботи стандартні. Вікно Mathcad містить головне меню, панелі інструментів і інші елементи управління. Головною відмітною рисою інтерфейсу є панель математичних інструментів. Кожна кнопка в математичній панелі інструментів, відкриває зв'язану з нею палітру інструментів. Призначення кнопок наведене в таблиці 1.1.
Таблиця 1.1
Прості обчислення
Хоча Mathcad призначений для складних математичних обчислень, його легко можна використовувати як простий калькулятор. Приклад такого типу обчислень описаний нижче по кроках: – після натискання в будь-якому місці робочого документа з'являється курсор, що має вигляд червоного хрестика. Усе введене з клавіатури буде розміщатися тепер у робочому документі, починаючи з місця розташування хрестика. – введіть із клавіатури: 15-8/104.5=. Після набору знака = виводиться результат 14.923. Mathcad відображає формули в тому вигляді, як їх друкують у книгах, тобто по всій площі екрана. Mathcad підбирає розміри для дужок, дробових рис і інших математичних символів так, щоб вони виглядали на екрані так, як це прийнято в літературі. Mathcad розуміє пріоритет виконання операцій. Після введення знака рівності = Mathcad показує результат. Символи операторів і операцій, що вставляються в робочий документ, містять поля введення. Поля введення призначені для введення чисел і виразів. Поле введення, що з'являється після обчисленого результату, використовується для вставки і перетворень одиниць виміру. Дані на екрані можна редагувати, установлюючи курсор у потрібному місці.
Визначення і змінні
Гнучкість і міць Mathcad стають зрозумілими при використанні змінних і функцій. За допомогою змінних і функцій стають можливими зв'язок рівнянь і використання проміжних результатів у подальших обчисленнях. Щоб визначити будь-яку змінну, необхідно: – надрукувати ім'я змінної, яку треба визначити; – надрукувати двокрапку, щоб ввести символ оператора присвоювання; – надрукувати значення, що привласнюється змінній. Значення може бути числом або виразом. Mathcad читає робочий документ зверху вниз і зліва направо. Визначивши змінну, її можна використовувати в обчисленнях скрізь нижче і праворуч оператора, в якому вона визначена.
Введення тексту
Для того, щоб ввести текст, потрібно клацнути у вільному місці і виконати пункт Text Region з меню Insert, або натиснути Shift+¢ на клавіатурі. Приклад введення тексту. Натисніть Shift+(, щоб сповістити Mathcad про початок введення тексту. Mathcad заміняє хрестик на вертикальну лінію, названу курсором введення. Курсор введення оточений рамкою із маркерами, що позначає текстову область. В міру введення тексту рамка буде розширюватися. Введення другого рядка відбувається після натискання клавіші Enter. Для виходу з текстової області необхідно клацнути в будь-якому місці робочого документа.
Області Mathcad
Mathcad допускає введення формул і тексту в будь-якому місці робочого документа. Кожний математичний вираз або фрагмент тексту є областю. Mathcad створює невидимий прямокутник, що містить кожну область. Робочий документ Mathcad є сукупність таких областей.
Повторювані обчислення
Mathcad може виконувати повторювані або ітераційні обчислення так само легко, як обчислення окремих виразів. З цією метою Mathcad використовує спеціальний тип змінних ‑ ранжовані змінні. Ранжована змінна приймає заданий діапазон значень. У найпростішому випадку для створення такої змінної використовується вираз: x:=0..10, де x приймає значення від 0 до 10 із кроком 1. Якщо у виразі присутня ранжована змінна, то Mathcad обчислює вираз стільки разів, скільки значень містить ця змінна.
Функції користувача
Ці функції створюються користувачем і забезпечують адаптацію Mathcad до розв'язуваних задач. Наприклад, для завдання функції користувача – введіть d(t):=; – завершите визначення функції, надрукувавши вираз
1600+a/2 [Space]*t^2 [Enter].
Форматування результату
У Mathcad можна установлювати формат виведення чисел, тобто змінювати число виведених десяткових знаків, змінювати експонентний вид зображення чисел на звичайний запис з десятковою крапкою і так далі. Для форматування необхідно зробити подвійне клацання по числу, і у вікні, що з'явилося, задати формат зображення чисел результату. Форматування можна виконати командою Result… з меню Format. При зміні формату виведення результатів, міняється тільки їх зовнішній вигляд. Внутрішнє зображення чисел у Mathcad завжди має подвійну точність з 15 знаками в мантисі.
Побудова графіків
Mathcad може будувати двовимірні графіки в декартових і полярних системах координат, картини ліній рівня, зображувати поверхні і виводити ряд інших тривимірних графіків. Щоб створити графік у Mathcad, потрібно клацнути мишею в тому місці, де його потрібно розмістити. Клацнути по кнопці з зображенням графіка в панелі математичних інструментів, у палітрі графіків вибрати тип графіка і клацнути по ньому. У порожньому шаблоні графіка, що з'явиться, треба заповнити поля введення функцій і аргументів, відображуваних по відповідних осях графіка. Приклади побудови різних графіків наведені в лабораторній роботі №3. На одному графіку можна зобразити кілька функцій, указавши їх у полі введення шаблона осі ординат через кому. Можлива побудова графіків функції двох змінних. Крім того, тут можна використовувати креслення і рисунки, отримані в інших графічних системах.
Прості операції При роботі з математичними виразами використовуються знаки додавання (+), віднімання (-), множення (*), ділення (/), піднесення в ступінь (^) і ін., наведені в табл.1.2. У таблиці показані послідовності набору клавіш і відповідні математичні формули на екрані. Наприклад, при обчисленні виразу в режимі калькулятора
3+4/117+sin(0.2)=3.233
після введення знака (=) з'являється розрахункова величина.
Таблиця 1.2
Продовження таблиці 1.2
Продовження таблиці 1.2
При наборі формул необхідно керуватися наступними правилами: 1. Усі коефіцієнти і змінні, вхідні у вираз, повинні бути попередньо визначені. 2. При наборі виразів, зв'язаних з операціями ділення, піднесення в ступінь і добування кореня для зміни порядку обчислень, варто використовувати круглі дужки. 3. Складні вирази доцільно обчислювати по частках. 4. Визначення коефіцієнтів і змінних повинні розташовуватися вище і ліворуч стосовно формул, у яких вони використовуються. 5. Бажано уникати буквених індексів, що часто використовують в інженерних і економічних розрахунках. Вбудовані функції
У пакеті широко використовуються убудовані функції. Ці функції визначені в самій системі і готові до негайного використання. До основних убудованих функцій відносяться тригонометричні і зворотні до них; логарифмічні, статистичні; перетворення Фур'є, функції Бесселя, комплексних змінних і ін. Повний список цих функцій і їхній опис можна одержати, вибравши пункт Function меню Insert. Приклади використання стандартних функцій містяться в довідковій документації, подивитися яку можна за допомогою вікна центра інформаційних ресурсів.
Доступ до зазначеного вікна здійснюється кнопкою Resource Center стандартної панелі інструментів.
ЛАБОРАТОРНІ РОБОТИ
У лабораторних роботах надані приклади розв'язання різних математичних задач. Варіанти індивідуальних завдань знаходяться в додатку. Фрагменти робочих документів Mathcad, що містяться в усіх нижче наведених прикладах, укладені в рамки.
Лабораторна робота №1
Порядок виконання 1. Обчислення значень виразів. Для обчислення значення виразу треба набрати його і ввести знак оператора простого виведення =:
При обчисленні виразів, що містять змінні, необхідно попередньо визначити ці змінні:
Математичні функції вводяться за допомогою: – шаблонів з палітри Calculator; – Insert|Function; – клавіатури
Шаблони інтеграла і похідної вводяться з палітри Calculus Toolbar. Поля введення заповнюються необхідними даними:
2. Операції з векторами. Вектори і матриці вводяться за допомогою шаблонів з палітри Vector and Matrix Toolbar:
Індекси елементів вектора вводяться символом [:
3. Операції з матрицями. Задано матриці А і В:
3.1. Визначник матриці.
3.2. Транспонування матриці. Транспонування виконується за допомогою шаблона з палітри Vector and Matrix Toolbar:
3.3. Одержання оберненої матриці.
3.4. Добуток матриць. Виконано перевірку обчислення оберненої матриці:
3.5. Обчислення матричного виразу.
Лабораторна робота № 2
Постановка задачі. Дано систему n лінійних алгебраїчних рівнянь з n невідомими:
Потрібно знайти її розв'язок, тобто таку сукупність значень невідомих x1, x2, …, xn, яка при підстановці в дану систему перетворює всі рівняння в тотожності.
Завдання Розв'язати систему лінійних алгебраїчних рівнянь, задану в матричній формі А*Х=У, де А і В матриці з лабораторної роботи №1.
Порядок виконання 1. Розв'язання методом Крамера.
2. Розв'язання методом Гаусса. За замовчуванням нумерація індексів елементів векторів або матриць починається з 0. Змінити початок нумерації можна за допомогою змінної ORIGIN:
Формування розширеної матриці системи:
Приведення матриці D до трикутного виду:
Виділення розв'язку вихідної системи з матриці С:
3. Розв'язання матричним методом.
4. Розв'язання за допомогою функції lsolve.
5. Розв'язання за допомогою блока Given... Find. Система рівнянь записана в загальноприйнятому вигляді; знак символьної рівності = вводиться з панелі Boolean:
Лабораторна робота № 3
Побудова графіків функцій
Завдання Використовуючи засоби Mathcad побудувати графіки: – у декартовій системі координат; – поверхні; – у полярній системі координат; – вставити рисунок формату.bmp. Порядок виконання 1. Побудова графіків у декартовій системі. Інтервал, що задається за умовчанням для змінної,– [-10..10], але можна задати інший інтервал, наприклад з кроком 0,01:
Для побудови графіка необхідно натиснути кнопку X-Y Plot панелі Graph Toolbar. У заготовці графіка, що з'явилася, варто ввести у відповідні поля функцію та її аргумент. Завершуємо побудову клацанням миші поза графіком:
Для одержання декількох функцій на одному графіку необхідно вводити у відповідні поля введення функції та їхні аргументи через коми. 2. Побудова графіків поверхні. 2.1. Графік гіперболоїда. Для швидкої побудови графіка поверхні необхідно визначити відповідну функцію користувача, а потім клацнути по кнопці Surface Plot панелі Graph Toolbar. У заготовці графіка, що з'явилася на екрані, варто ввести ім'я функції без указівки її аргументів (якщо функцій декілька, вони перелічуються через кому):
2.2. Побудова поверхні сфери. Визначаємо функції користувача:
При побудові графіка, функції X,Y,Z необхідно обов'язково записати в дужках!
2.3. Побудова поверхні, отриманої обертанням функції навколо осі Х.
Поверхня S отримана в результаті обертання графіка функції f(x) навколо осі абсцис на відрізку [a,b]:
3. Побудова графіків у полярних координатах. 3.1. Побудова крапки з координатами r і α.
3.2. Побудова графіка функції.
4. Вставка рисунків формату bmp. Рисунки, що вставляються, повинні знаходиться в поточному каталозі або необхідно вказати повне ім'я файлу, включно шлях і розширення. Для вставки рисунка потрібно вибрати пункт Picture меню Insert і в заготовці рисунка, що з'явиться, вписати ім'я файлу формату bmp у лапках:
Лабораторна робота № 4 Лабораторна робота № 5
Розв'язання системи нелінійних рівнянь
Постановка задачі Розглянемо систему n нелінійних рівнянь з n невідомими fi(x1, x2, …, xn) = 0 (i = 1, 2, …, n), де fi – деякі алгебраїчні або трансцендентні функції. Позначивши x = (x1, x2, …, xn) і f = (f1, f2, …, fn), систему нелінійних рівнянь запишемо у векторній формі
f (x) = 0.
Розв'язання даної системи нелінійних рівнянь полягає у знаходженні таких векторів х, що перетворюють систему в тотожність. Завдання
Дано систему нелінійних рівнянь:
Розв'язати цю систему: 1) графічним методом; 2) за допомогою розв'язувального блока Given... Find.
Порядок виконання
1. Графічне розв'язання. З першого рівняння виражаємо y через x. Оскільки з y добувається квадратний корінь, то одержимо дві залежності – ya(xa) і yb(xb). З другого рівняння виразимо x через y. Отриману залежність позначимо y1(x1). Визначимо функції користувача:
Інтервал по осі ординат був установлений вручну:
Розв'язок знаходиться у вікні інструмента X-Y Trace:
x=0,53656; y=2,3442. 2. Розв'язання за допомогою блока Given... Find. Початкові наближення вибираємо з графічного розв'язання:
Лабораторна робота № 6
Лабораторна робота № 7
Лабораторна робота №8 Інтерполяція функцій
Постановка задачі Нехай деяка функція y = f(x) задана таблицею
Потрібно знайти многочлен Pn(x) ступеня n, що приймає в заданих точках xi (i = 0, 1, 2, …, n) ті ж значення, тобто такий, що
Pn(xi) = f(xi) = yi (i = 0, 1, 2, …, n)...
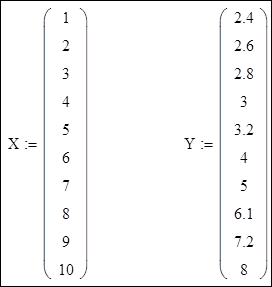
Завдання Дано функцію в табличному вигляді, необхідно: 1. Одержати інтерполяційний многочлен Лагранжа. 2. Записати інтерполяційний многочлен у загальному виді. 3. Виконати інтерполяцію методом Ван-дер-Монда. 4. Виконати інтерполяцію за допомогою вбудованих функцій. 5. Обчислити наближені значення функції в трьох міжвузлових точках. 6. Побудувати графіки заданої функції й отриманих інтерполяційних многочленів.
Порядок виконання Вихідні дані:
1. Використовуючи формулу Лагранжа, складемо інтерполяційний многочлен.
Спростимо інтерполяційний многочлен, застосувавши директиви simplify і float панелі symbolic keyword toolbar:
2. Інтерполяційний многочлен у загальному вигляді.
3. Побудова інтерполяційного многочлена методом Ван-дер-Монда.
4. Інтерполяція за допомогою вбудованих функцій. 4.1. Лінійна інтерполяція.
4.2. Кубічна сплайн-інтерполяція.
5. Значення функції в трьох міжвузлових точках: Х1=1,5; Х2=2,5; Х3=7,5.
6. Побудова графіків вихідної залежності X-Y і функцій f1(x), f4(x), f5(x).
Лабораторна робота № 9
Постановка задачі Задача наближення (апроксимації) полягає в заміні функціональної залежності, заданої на множині XÍR у вигляді таблиці, графіка, формули або в неявному вигляді, більш простою наближуваною функцією. Найбільш ефективним методом побудови найкращого середнього квадратичного наближення є метод найменших квадратів. Завдання
Виконати апроксимацію функції, заданої в табличному вигляді многочленами першого і другого ступеня. Порядок виконання Вихідні дані:
1. Лінійна апроксимація функції. 1.1. Визначення коефіцієнтів апроксимуючого многочлена першого ступеня y=a+bx. Система нормальних рівнянь:
Кількість пар даних:
Розв'язання:
1.2. Визначення коефіцієнтів a, b за допомогою функцій intercept і slope.
Залежність між Xi і Yi близька до лінійного, тому що коефіцієнт кореляції r близький до 1:
Визначаємо апроксимуючу функцію:
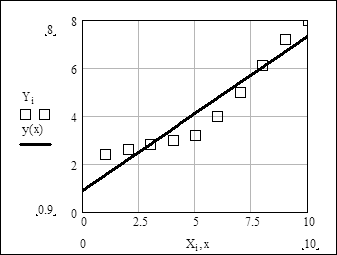
Графіки апроксимуючого многочлена і вихідних точок:
2. Квадратична апроксимація. У якості вихідних даних візьмемо табличну залежність з 1-го пункту. Шукаємо апроксимуючу функцію у виді:
Ступінь многочлена:
Визначаємо коефіцієнти апроксимуючого многочлена:
Задамо діапазон зміни х такий же, як і для вектора Х:
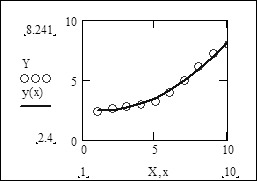
Побудуємо графіки табличної залежності X-Y і апроксимуючого многочлена y(x):
Для оцінки якості отриманого розв'язку обчислимо коефіцієнт варіації:
Помітимо, що функція regress може бути використана для визначення коефіцієнтів апроксимуючих многочленів більш високого ступеня. Однак використовувати многочлени ступеня вище п'ятого не рекомендується.
Лабораторна робота № 10 ДОДАТОК
СПИСОК ЛІТЕРАТУРИ 1. Дьяконов В. П. Mathcad 2001: учебный курс. – СПб.: Питер, 2001. – 624 с. 2. Дьяконов В. П., Абраменкова И. В. Mathcad 8 PRO в математике, физике и в Internet. – М.: «Нолидж», 1999. – 512 с. 3. Очков В. Ф. Mathcad 8 Pro для студентов и инженеров. – М.: КомпьютерПресс, 1999. – 238 с. 4. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Физматгиз, 1970. – 664 с. 5. Березин И.С., Жидков Н.П. Методы вычислений. – М.:Наука, 1981. – 632 с. 6. Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М. Методы оптимизации. – М.: Наука, 1978. – 526 с. 7. Щуп Т. Решение инженерных задач на ЭВМ. – М.: Радио и связь, 1984. – 238 с. 8. Таха Х. Введение в исследование операций. Пер. с англ. Кн. 1,2. – М.: Мир, 1985. – Кн.1 – 479 с., Кн.2 – 496 с. 9. Кафаров В.В. Методы кибернетики в химии и химической технологии: Учебник для вузов. 4-е изд. – М.: Химия, 1985. – 448 с. 10. Бондарь А.Г. Математическое моделирование в химической технологии. – К: Вища шк., 1973. – 280 с. 11. Скурихин В.И. и др. Математическое моделирование. – Киев: Техника, 1983. – 270 с. 12. Линейное и нелинейное программирование. Под ред. И.Н. Лященко. – К: Вища шк., 1975. – 371 с. 13. Кандзюба С.П., Прокопченко А.В. Методические указания по курсу «Исследование операций». – Днепропетровск: УГХТУ, 1998. – 103 с. 14. Прокопченко А.В., Філатова К.И. Методичні вказівки та індивідуальні завдання для самостійної роботи з курсу «Економіко–математичні методи». – Дніпропетровськ: УДХТУ, 1994. – 48 с. 15. Прокопченко А.В., Анофрієв П.Г. Методичні вказівки до виконання лабораторних робіт з курсу “Математичні методи та моделі в розрахунках на ЕОМ” у середовищі Mathcad. – Дніпропетровськ: УДХТУ, 2000. – 57 с.
ЗМІСТ
ВСТУП................................................................................................... 3 РОБОТА В СЕРЕДОВИЩІ Mathcad.................................................... 4 Прості обчислення................................................................................. 5 Визначення і змінні............................................................................... 5 Введення тексту..................................................................................... 5 Області Mathcad.................................................................................... 6 Повторювані обчислення...................................................................... 6 Функції користувача............................................................................. 6 Форматування результату.................................................................... 6 Побудова графіків................................................................................. 7 Збереження файлів, друк і вихід з Mathcad......................................... 7 Прості операції...................................................................................... 7 Вбудовані функції................................................................................. 9 ЛАБОРАТОРНІ РОБОТИ..................................................................... 10 Лабораторна робота №1. Прості обчислення. Операції з векторами і матрицями......................................................................................................................... 10 Лабораторна робота № 2. Розв'язання системи лінійних алгебраїчних рівнянь 13 Лабораторна робота № 3. Побудова графіків функцій...................... 15 Лабораторна робота № 4. Розв’язання нелінійних рівнянь............... 19 ВСТУП
Методичні вказівки містять стислі відомості про популярну систему комп'ютерної математики Mathcad, яка бурхливо розвивається. Розглянуто інтерфейс системи, технологія розв'язання різних задач і візуалізація результатів. Надані завдання і зразки виконання лабораторних робіт з необхідними зауваженнями, коментарями, таблицями і рисунки з різних розділів математики – від матричної алгебри до розв'язання диференціальних рівнянь і апроксимації. Методичні вказівки призначені для студентів і аспірантів, що займаються вивченням математичних методів і застосуванням систем комп'ютерної математики для розв'язання науково-технічних і інженерних задач. Одна з задач ПЕОМ – автоматизація інтелектуальної праці, підвищення ефективності наукових досліджень. З цією метою розробляються математичні пакети прикладних програм, які розраховані на широкі кола фахівців. До подібних пакетів належать Mathcad, Mathematica, MatLab+Simulink, Maple, Eureka, Gauss та ін. Mathcad – універсальний математичний пакет, призначений для виконання інженерних і наукових розрахунків. Основна перевага пакета – загальноприйнята математична мова, на якій формулюються розв'язувані задачі. Об'єднання текстового редактора з можливістю використання загальноприйнятої математичної мови дозволяє користувачеві одержати готовий підсумковий документ. Пакет має широкі графічні можливості, розширювані від версії до версії. До достоїнств Mathcad можна віднести: – простота у використанні і легкість у навчанні. Більшість дій, необхідних для управління програмою, є інтуїтивно прозорими, і на освоєння її можливостей людині, що працювала раніше в середовищі Windows, потрібно небагато часу; – можливість виконання обчислень високого ступеня складності. Крім звичних чисельних розрахунків система здатна робити символьні перетворення, наприклад:
– широкі графічні можливості. Велика кількість типів графіків полегшують візуалізацію даних; – інтеграція з Internet, що дозволяє використовувати фрагменти розрахунків, збережені в надрах його безмережних інформаційних ресурсів; – підтримка технології OLE; – наявність текстового редактора, що підтримує інтерфейс WYSIWYG. Це дозволяє готувати звіти, статті і технічну документацію прийнятної якості, не виходячи з Mathcad. РОБОТА В СЕРЕДОВИЩІ Mathcad Для запуску Mathcad необхідне подвійне клацання по піктограмі Mathcad, він викликає появу заставки. Потім відкривається вікно застосування.
Пакет Mathcad – повноцінне Wіndоws-застосування, тому правила і прийоми роботи стандартні. Вікно Mathcad містить головне меню, панелі інструментів і інші елементи управління. Головною відмітною рисою інтерфейсу є панель математичних інструментів. Кожна кнопка в математичній панелі інструментів, відкриває зв'язану з нею палітру інструментів. Призначення кнопок наведене в таблиці 1.1.
Таблиця 1.1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 545; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.015 с.) |

 ;
;




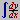




 треба виконати наступні дії:
треба виконати наступні дії:
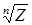

 , якщо всі елементи v - дійсні
, якщо всі елементи v - дійсні

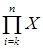





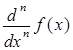



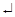 ]
]