
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 2. Нелінійна регресія. Множинна лінійна регресіяСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Деякі види нелінійної регресії
Якщо рівняння регресії Розглянемо, наприклад, параболічну регресію другого порядку
де Як і у випадку лінійної регресії, використовуємо метод найменших квадратів. Відповідно до цього методу ми будуємо функцію
тобто
Для відшукання її найменшого значення дорівнюємо нулю її частинні похідні:
У цьому випадку одержимо наступну нормальну систему:
Знайдені із системи параметри Приведемо нормальні системи для знаходження невідомих параметрів деяких інших типів рівнянь регресії. 1. Нормальна система має вигляд:
2.
Приклад. Собівартість одиниці продукції перебуває (за інших рівних умов) у зворотній залежності до числа одиниць, що випускаються. На підставі наведених в таблиці 18 даних скласти залежність між собівартістю й числом одиниць, що випускаються, якщо рівняння регресії має вигляд Таблиця 18
Розв’язання. Складемо розрахункову таблицю 19 для знаходження даних, що знаходяться в системі (2.1.3)
Таблиця 19
У такий спосіб маємо систему:
Розв’язавши цю систему, знайдемо a = 14,9, b = 5333,3.
Отже,
Кореляційне відношення
При оцінці тісноти нелінійного зв'язку можна використовувати наступні міркування. Нехай дані спостережень над кількісними ознаками Таблиця 20
До першої групи віднесемо 10 значень До другої групи віднесемо ті 20 значень Умовні середні тепер можна назвати груповими середніми: групова середня першої групи Введемо міжгрупове середнє квадратичне відхилення Як уже говорилося, на зміну ознаки
характеризує частку розсіювання величини Кореляційним відношенням
де У формулі (2.2.1)
де п – сума всіх частот (об'єм вибірки),
Аналогічно визначається кореляційне відношення
Розглянемо деякі властивості кореляційного відношення. 1. 2. Якщо 3. Ознака 4. Кореляційне відношення не менше абсолютної величини коефіцієнта кореляції:
5. Між ознаками
Можна довести, що при зростанні кореляційного відношення зв'язок У процесі доведення вищевказаних властивостей ніде не приймається в увагу вид кореляційного зв'язку між Американський математик ХХ в. Чеддок запропонував наступну таблицю 21 якісної оцінки тісноти зв'язку: Таблиця 21
Приклад. Знайти рівняння регресії
Таблиця 22
Розв’язання. Складемо розрахункову таблицю 23 для знаходження даних, що входять у систему (2.1.2): Таблиця 23
Підставимо числа, що знаходяться в останньому рядку таблиці 23, у систему (2.1.2):
Розв’язавши цю систему (наприклад, методом Гаусса), знайдемо:
Шукане рівняння регресії має вигляд:
Для обчислення кореляційного відношення
Значення
Тут значення
Шукане кореляційне відношення дорівнює:
Якщо використовувати таблицю 21, то кореляційний зв'язок досить високий. Множинна лінійна кореляція
До цього пункту розглядався кореляційний зв'язок між двома ознаками (йього іноді називають парним). Перед дослідником часто виникає питання про вивчення так званої множинної кореляції, тобто кореляційної залежності даної ознаки від декількох факторів – ознак. У найпростішому випадку число ознак дорівнює трьом і зв'язок між ними лінійний:
Тут У цьому випадку виникають наступні задачі: 1) знайти по даним спостережень коефіцієнти регресії 2) оцінити тісноту зв'язку між 3) оцінити тісноту зв'язку між Як же розв’язуються ці задачі методами математичної статистики? Скористаємося для ілюстрації даними таблиці 24. Таблиця 24
Переглядаючи ці дані, можна бачити, що ступінь взбитости морозива (як одного з найважливіших показників його якості) залежить як від часу його фризерування (заморожування суміші для морозива), так і від його температури при випуску із фризера. Можна статистично визначити тісноту зв'язку взбитости морозива з першим і другим факторами, обчислюючи коефіцієнти кореляції. Коефіцієнт кореляції між взбитістю морозива і часом його фризерування обчислений нижче (див. формули (1.6.3) і (1.6.4)) Необхідні розрахункові дані наведені в таблиці 25. Таблиця 25
Таким чином, коефіцієнт кореляції свідчить про прямий і дуже тісний зв'язок між взбитістю морозива і часом його фризерування. Далі можна обчислити коефіцієнт кореляції між взбитістью морозива і його температурою при випуску із фризера (показники температури беруться в їхньому абсолютному значенні: ріст цього значення розглядається як збільшення «холоду»). Проміжні розрахунки наведені в таблиці 26.
Таблиця 26
Залежність взбитости морозива від його температури також дуже тісна. Чим нижче температура, тобто чим більше «холод», тим вище ступінь взбитости морозива. Як же впливають на ступінь взбитости морозива обидві умови одночасно: час фризерування і температура морозива при випуску його із фризера? Для того, щоб відповісти на це питання, необхідно обчислити сукупний коефіцієнт кореляції, або, як його ще називають, коефіцієнт множинної кореляції. Цей коефіцієнт можна визначити як кореляційне відношення, маючи на увазі рівняння лінії регресії
Порівняйте цю формулу з формулою (2.2.1) Спочатку знайдемо рівняння регресії
Для знаходження параметрів цього рівняння необхідно скласти наступну систему нормальних рівнянь:
яка випливає з методу найменших квадратів. Всі необхідні дані для складання цих рівнянь, за винятком
Система нормальних рівнянь має вигляд:
У результаті розв’язання системи одержимо:
Таким чином, зв’язок збитости морозива з часом його фрезерування і його температурою при випуску із фризера, має вигляд:
Підставивши в це рівняння відповідні значення
Звідси
Вище була обчислена необхідна для визначення середнього квадратического відхилення
Сукупний коефіцієнт кореляції знайдемо по формулі (2.3.2):
Сукупний коефіцієнт кореляції свідчить про те, що взбитість морозива значною мірою визначається спільним впливом часу фризерування і температури морозива при виході із фризера. Треба, однак, відзначити, що цей коефіцієнт мало відрізняється від обчислених вище коефіцієнтів, що характеризують залежність взбитости морозива від кожної із двох зазначених умов окремо, Для того, щоб відповісти на це питання, необхідно обчислити коефіцієнт кореляції між самими умовами - тривалістю фризерування і температурою морозива після фризерування. Цей коефіцієнт такий:
Як і слід було очікувати, між самими умовами, що визначають, збитість морозива, існує дуже тісний зв'язок: чим тривалеіше фризерування морозива, тим нижче його температура після виходу із фризера. Наявність тісного зв'язку між ознаками - факторами вплинуло й на величину сукупного показника. Ці ознаки піддаються настільки сильному взаємному впливу, що коефіцієнт кореляції взбитости морозива з одним з них є в сутності показником тісноти зв'язку з обома. Зрозуміло, що за таких умов характеристика тісноти зв'язку з обома ознаками - факторами одночасно повинна мало відрізнятися від характеристики тісноти зв'язку з кожним фактором окремо, тому що включення другого з них у кореляційний аналіз практично нічого додаткового не дає. Описуване положення стане ще більше ясним, якщо на додаток до зробленого аналізу обчислити так звані частинні коефіцієнти кореляції. Ці частинні коефіцієнти відрізняються від звичайних (повних) коефіцієнтів тим, що при їхньому вирахуванні кореляція між двома ознаками визначається при усуненні впливу на них третьої ознаки (якщо в аналіз вводяться три ознаки). У розглянутому випадку частинний коефіцієнт кореляції між ступенем взбитости морозива й тривалістю фризерування буде отриманий, якщо усунути вплив на обидві ці ознаки температури морозива при виході його із фризера. При усуненні ж впливу тривалості фризерування як на взбитість морозива, так і на його температуру після фризерування буде отриманий інший частинний коефіцієнт кореляції вже між двома цими ознаками. Якщо обчислені «звичайні» (повні) коефіцієнти кореляції
Значок ліворуч від температурою при виході із фризера, одержуємо наступні результати:
Частинний коефіцієнт кореляції між взбитістю морозива і тривалістю фризерування Другий частинний коефіцієнт кореляції, що характеризує зв'язок між взбитістью морозива і його температурою при випуску із фризера, невеликий ( Сукупний коефіцієнт кореляції визначався вище у вигляді кореляційного відношення після визначення лінії регресії Сукупний коефіцієнт кореляції пов'язаний з повними коефіцієнтами між парами ознак так:
Якщо підставити в цю формулу значення повних коефіцієнтів кореляції між парами ознак, то вийде
Значення
Підставивши значення зазначених коефіцієнтів, одержимо:
У висновку ще раз підкреслимо, що введені коефіцієнти, як і «звичайний» коефіцієнт кореляції, служать для оцінки лінійного зв'язку між ознаками, причому
Рангова кореляція
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 985; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.60.175 (0.013 с.) |

 або
або  не є лінійними, то регресію називають нелінійною, або криволінійною. Теорія нелінійної регресії розглядає ті ж задачі, що й теорія лінійної регресії, тобто встановлення форми й тісноти кореляційного зв'язку.
не є лінійними, то регресію називають нелінійною, або криволінійною. Теорія нелінійної регресії розглядає ті ж задачі, що й теорія лінійної регресії, тобто встановлення форми й тісноти кореляційного зв'язку.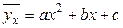 , (2.1.1)
, (2.1.1) ,
,  ,
,  – невідомі параметри, які треба знайти.
– невідомі параметри, які треба знайти. ,
, .
.
 (2.1.2)
(2.1.2) (гіперболічна регресія).
(гіперболічна регресія). (2.1.3)
(2.1.3) (логарифмічна регресія).
(логарифмічна регресія). (2.1.4)
(2.1.4)




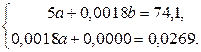
 .
.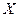 і
і  зведені в кореляційну таблицю 20.
зведені в кореляційну таблицю 20.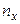

 .
. .
. групова середня другої групи
групова середня другої групи 
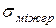 – середнє квадратичне відхилення умовних (групових) середніх
– середнє квадратичне відхилення умовних (групових) середніх  , а також загальне середнє квадратическое відхилення
, а також загальне середнє квадратическое відхилення  – середнє квадратическое відхилення значень ознаки всієї сукупності щодо загальної середньої.
– середнє квадратическое відхилення значень ознаки всієї сукупності щодо загальної середньої. . Деяку частину
. Деяку частину  Тому величина
Тому величина
 може служити характеристикою тісноти кореляційного зв'язку між ознаками у вибірці.
може служити характеристикою тісноти кореляційного зв'язку між ознаками у вибірці. , (2.2.1)
, (2.2.1) =
= 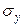 =
= 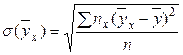 , (2.2.2)
, (2.2.2) , (2.2.3)
, (2.2.3) – частота значення
– частота значення  ,
, – загальна середня ознаки
– загальна середня ознаки  – умовна середня ознаки
– умовна середня ознаки  .
.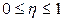 .
. , то ознака
, то ознака  .
. .
.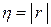 .
. до нуля, тим зв'язок слабкіше; ніж ближче
до нуля, тим зв'язок слабкіше; ніж ближче  за даними, наведеними у кореляційній таблиці 22. Оцінити силу кореляційного зв'язку по кореляційному відношенню.
за даними, наведеними у кореляційній таблиці 22. Оцінити силу кореляційного зв'язку по кореляційному відношенню.
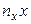




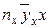





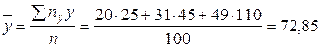 .
.
 дорівнює
дорівнює
 .
.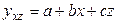 (2.3.1)
(2.3.1) - функція,
- функція,  - аргументи.
- аргументи.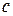 , параметр а;
, параметр а; ,
,  ;
;




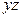


 . (2.3.2)
. (2.3.2)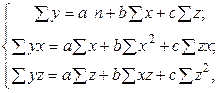
 , знайдені при обчисленні коефіцієнтів кореляції
, знайдені при обчисленні коефіцієнтів кореляції  і
і  . Обчислимо
. Обчислимо 

 50,3244;
50,3244; 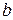 =3,05;
=3,05; -0,1841.
-0,1841.
 можна визначити середнє квадратическое відхилення
можна визначити середнє квадратическое відхилення  , потрібне для обчислення сукупного коєффициента кореляції
, потрібне для обчислення сукупного коєффициента кореляції
 .
. .
.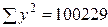 (див. таблицю 25). Отже,
(див. таблицю 25). Отже, .
.
 і
і  . Таким чином, виявляється, що ступінь тісноти зв'язку досліджуваної ознаки з кожною з вищевказаних умов майже така ж, як і у випадку, коли ця ознака корелюється з обома цими умовами одночасно. Чим же це обумовлено?
. Таким чином, виявляється, що ступінь тісноти зв'язку досліджуваної ознаки з кожною з вищевказаних умов майже така ж, як і у випадку, коли ця ознака корелюється з обома цими умовами одночасно. Чим же це обумовлено?
 (2.3.3)
(2.3.3) (2.3.4)
(2.3.4) позначає фактор, вплив якого усунуто. Обчислюючи по цих формулах частинні коефіцієнти між ступенем взбитости морозива і тривалістю фризерування, а також між ступенем взбитости морозива і його
позначає фактор, вплив якого усунуто. Обчислюючи по цих формулах частинні коефіцієнти між ступенем взбитости морозива і тривалістю фризерування, а також між ступенем взбитости морозива і його ;
; .
. значно менше повного коефіцієнта (
значно менше повного коефіцієнта ( ). Повний коефіцієнт кореляції між цими ознаками дорівнював
). Повний коефіцієнт кореляції між цими ознаками дорівнював  . Зіставлення цих двох показників дозволяє зробити наступний висновок: коли корелювалися ступінь взбитости морозива з його температурою, те ця ознака ставилася у зв'язок не стільки з температурою, скільки із тривалістю фризерования. Температура морозива при випуску його із фризера є показником, який залежить від часу фризерування: чим більше час фризерування, тим нижче температура. Отже, при корелюванні взбитости морозива з його температурою через останню робила свій вплив і тривалість фризерування. Це з очевидністю і виявилося при обчисленні частинного коефіцієнта кореляції, коли «чистий» вплив температури при усуненні впливу тривалості фризерування виявився дуже слабким. Можна сказати, що введення в аналіз такого показника, як температура морозива, з'явилося взагалі зайвим, оскільки він носить лише похідний характер.
. Зіставлення цих двох показників дозволяє зробити наступний висновок: коли корелювалися ступінь взбитости морозива з його температурою, те ця ознака ставилася у зв'язок не стільки з температурою, скільки із тривалістю фризерования. Температура морозива при випуску його із фризера є показником, який залежить від часу фризерування: чим більше час фризерування, тим нижче температура. Отже, при корелюванні взбитости морозива з його температурою через останню робила свій вплив і тривалість фризерування. Це з очевидністю і виявилося при обчисленні частинного коефіцієнта кореляції, коли «чистий» вплив температури при усуненні впливу тривалості фризерування виявився дуже слабким. Можна сказати, що введення в аналіз такого показника, як температура морозива, з'явилося взагалі зайвим, оскільки він носить лише похідний характер.

 збіглося з обчисленим раніше по формулі (2.3.2). Із частинними коефіцієнтами кореляції сукупний коефіцієнт кореляції зв'язаний наступною формулою:
збіглося з обчисленим раніше по формулі (2.3.2). Із частинними коефіцієнтами кореляції сукупний коефіцієнт кореляції зв'язаний наступною формулою:
 .
.



