
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коефіцієнт рангової кореляції СпирменаСодержание книги
Поиск на нашем сайте
Суть і методику рангової кореляції розкриємо на конкретному прикладі. Допустимо, що потрібно визначити тісноту зв'язку між виходом пшеничного хліба й вологістю борошна на підставі наступних даних (таблиця 27).
Таблиця 27
Якщо говорити про вплив на вихід хліба тільки вологості борошна, то при збільшенні вологості вихід хліба повинен зменшуватися. Це зрозуміло: більш сухе борошно дає більший припік, тісто з нього не липне до машин, не розпливається при випічці. Однак дані наведених спостережень показують, що в ряді випадків зменшення виходу хліба переміняється його збільшенням. Це відбувається тому, що крім основного досліджуваного фактору (вологості борошна) на вихід хліба впливали й різні інші причини, не враховані в досліді. Вони й викликали випадкові стосовно дії основного фактору відхилення. Порушення загальної тенденції зменшення виходу хліба при збільшенні вологості борошна можуть бути легко встановлені, якщо розставити порядкові номери по зростанню або по убуванню ознак. Ці порядкові номери називаються рангами. Для ознаки Значенню
Таблиця 28
Таким чином, не можна відзначити строгу «правильність» у зміні рангів обох ознак. Найменшому значенню Для того, щоб виміряти тісноту зв'язку між цими двома ознаками, можна сконструювати показник, заснований на обліку рангів обох ознак. Обчислимо різниці між рангами
Значення суми квадратів різниць між рангами в середньому для цих двох випадків означало б, мабуть, відсутність зв'язків. Це середнє значення дорівнює Показник тісноти зв'язку сконструйований так, щоб показати, як відрізняється дійсна сума квадратів різниць між рангами від цього випадку відсутності зв'язку. Цей показник такий:
Він називається коефіцієнтом рангової кореляції Спирмена. Якщо зв'язок функціональний і прямий, то У розглянутому прикладі обчислимо
Таблиця 29
По формулі (2.4.1)
Показник кореляції рангів свідчить про досить тісний зв'язок між виходом хліба й вологістю борошна. Цей висновок можна зробити за умови значущості
Зауваження 1 Існують і інші показники тісноти зв'язку (наприклад, коефіцієнт рангової кореляції Кендалла). Зауваження 2 Коефіцієнти рангової кореляції є досить недосконалими статистичними характеристиками тісноти кореляційної залежності, тому що вони враховують не значення величин, а лише їхні ранги. У цьому плані вони значно уступають коефіцієнту кореляції й кореляційному відношенню. Однак на практиці нерідко доводиться визначати тісноту зв'язку між якісними ознаками, тобто такими, які не мають кількісного вираження або його важко встановити, але ці величини можна розташувати в порядку зростання або убування якості. Це значить, що їм можна приписати ранги. У цих випадках для оцінки ступеня зв'язку досліджуваних ознак застосовують коефіцієнт рангової кореляції.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 487; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.0.175 (0.009 с.) |

 )
)
 )
)
 (ранг1) відповідає
(ранг1) відповідає  (ранг8), значенню
(ранг8), значенню  (ранг2) відповідає
(ранг2) відповідає  (ранг10) і т.д. Ранги ознаки
(ранг10) і т.д. Ранги ознаки  . Такий збіг рангів міг би означати зв'язок функціональний, тобто такий, при якій зміни однієї ознаки цілком визначалися б зміною іншої. При цьому зв'язок був би прямий, тобто зміна обох ознак відбувалась би майже у ту саму сторону. При зв'язку ж функціональному, але зворотному, тобто такому, при якому зміни ознак, що зіставляються, відбуваються у різні сторони, як можна показати,
. Такий збіг рангів міг би означати зв'язок функціональний, тобто такий, при якій зміни однієї ознаки цілком визначалися б зміною іншої. При цьому зв'язок був би прямий, тобто зміна обох ознак відбувалась би майже у ту саму сторону. При зв'язку ж функціональному, але зворотному, тобто такому, при якому зміни ознак, що зіставляються, відбуваються у різні сторони, як можна показати,  , де
, де  - число пар значень порівнюваних ознак.
- число пар значень порівнюваних ознак.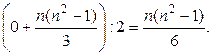
 . (2.4.1)
. (2.4.1)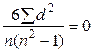 , тому що
, тому що  . Якщо ж зв'язок функціональний і зворотний, то
. Якщо ж зв'язок функціональний і зворотний, то  , тому що
, тому що  . Отже,
. Отже,  може приймати значення від 1 до -1. При цьому чим тісніше зв'язок між досліджуваними ознаками, тим ближче значення
може приймати значення від 1 до -1. При цьому чим тісніше зв'язок між досліджуваними ознаками, тим ближче значення  (таблиця 29)
(таблиця 29)
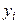



 .
.


