
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Регресії методом найменших квадратівСодержание книги
Поиск на нашем сайте
У найпростішому випадку різні значення
Загалом кажучи, теоретичні значення Напрошується наступна думка. Для різних Чи підтримуєте ви такий принцип мінімізації? Такий принцип правильним бути не може. Справа в тому, що відхилення Щоб не враховувати знаки відхилень, німецький математики К.Гаусс (1777-1855), французькі математики П. Лаплас (1749-1827) і А. Лежандр (1752-1833) незалежно друг від друга розробили метод найменших квадратів, відповідно до якого параметри
тобто у цьому випадку функції
Як відомо з курсу математичного аналізу, необхідною умовою екстремуму функції, яка має похідну, є рівність нулю частинних похідних:
Ці рівності можна розглядати як рівняння відносно Надалі для зручності запису замість
Зауваження 1. Цю систему легко запам'ятати. Візьмемо рівняння Можна довести, що при значеннях Розв’язок системи (1.4.2.3), має вигляд:
По цих формулах можна відразу знайти значення
Зауваження 2. У рівнянні лінійної регресії
коефіцієнт
і
відповідно. Метод (принцип) найменших квадратів перебуває в повній відповідності із загальним положенням математичної статистики, відповідно до якого як міра розсіювання береться дисперсія
Це говорить про те, що в середньому додатні відхилення врівноважують негативні. У математичній статистиці доведене аналогічне твердження: сума добутків відхилень
Щоб не враховувати знаки відхилень, як характеристика розкиду випадкової величини біля її математичного сподівання в теорії ймовірностей прийнята дисперсія:
У математичній статистиці це визначення приймає наступний вид:
де
Приклад. У результаті спостереження над дослідними ділянками була встановлена наступна врожайність (у ц с 1 га) при різній кількості внесених у ґрунт добрив (таблиця 1) Таблиця 1
Досвід показує, що в певних межах залежність між урожайністю й кількістю внесених добрив близька до лінійної (перевірте це геометрично для проведених даних). Знайти рівняння регресії Розв’язання. Шукаємо рівняння у вигляді
Складемо розрахункову таблицю 2.
Таблиця 2
По формулах (1.4.2.4) і (1.4.2.5) знайдемо параметри
Отже, шукане рівняння регресії має вигляд:
Як ми вже відзначали в пункті 1.2, це рівняння, як і будь-які інші отримані рівняння регресії, потрібно піддати регресійному й кореляційному аналізу.
1.5. Двовимірна дискретна випадкова величина і її закон розподілу. Кореляційна таблиця У теорії ймовірностей при опису багатьох випадкових явищ доводиться використовувати не одну, а кілька випадкових величин. Наприклад, точка влучення снаряда визначається двома випадковими величинами: абсцисою та ординатою. При імовірнісному моделюванні структури витрат родини необхідно розглядати в комплексі витрати випадково обраної родини на харчування, одяг, транспорт і т.д. Під Говорять також, що Для вивчення системи випадкових величин недостатньо вивчити окремо кожну складову системи. Тут виникає потреба вивчення взаємних зв'язків між ними, що приводить до нових задач, які не виникали при розгляді “звичайних”, одномірних випадкових величин. Надалі ми будемо говорити про двовимірну дискретну випадкову величину Законом розподілу дискретної двовимірної випадкової величини Нехай випадкова величина Звичайно закон розподілу двовимірної дискретної випадкової величини задають у вигляді таблиці із двома входами (таблиця 3).
Таблиця 3
Тому що випадкова величина
Знак подвійної суми – це повторне застосування символу підсумовування. Дійсно, якщо розкрити спочатку символ
Тепер розкриємо символ
Одержали суму ймовірностей, що стоять у всіх клітках таблиці 3. При перестановці символів підсумовування міняється лише порядок доданків. У таблиці 3 кожному з Нехай у результаті кожного з п випробувань ми реєструємо по одному значенню досліджуваних нами величин
можна розглядати як випадкову вибірку з генеральної сукупності всіх можливих значень двовимірної дискретної випадкової величини Таблиця 4
У верхньому рядку таблиці зазначені спостережувані значення ознаки
де Таблиця 4 називається кореляційною таблицею частот або просто кореляційною таблицею. Якщо в таблиці 4 частоти Очевидно, що
У таблиці 4 кожному спостережуваному значенню Кореляційна таблиця відносних частот є статистичним аналогом закону розподілу дискретної двовимірної випадкової величини (див. таблицю 3). Якщо ми хочемо за результатами досить великої кількості спостережень скласти імовірнісну модель випадкової величини Для приклада складемо кореляційну таблицю по вибірці, представленої в таблиці 5. Таблиця 5
Розташувавши значення Таблиця 6
Відповідна кореляційна таблиця відносних частот має такий вигляд (таблиця 7):
Таблиця 7
Коефіцієнт кореляції
У теорії ймовірностей було доведено, що математичне сподівання добутку двох незалежних випадкових величин дорівнює добутку їхніх математичних сподівань:
або
Тому, якщо для двох випадкових величин виявиться, що
те це є ознакою того, що між Недоліком запропонованої числової характеристики тісноти зв'язку є те, що її розмірність дорівнює добутку размірностей
де
Аналогом математичного сподівання в математичній статистиці є середня величина, тому чисельник у формулі (1.6.2) запишеться у вигляді
Після приведення до загального знаменника одержуємо статистичний аналог формули (1.6.2):
По цій формулі й обчислюється коефіцієнт кореляції в математичній статистиці. Середні квадратические відхилення, як відомо, мають такий вигляд:
Це статистичний аналог відповідної величини в теорії ймовірностей:
Перелічимо деякі властивості коефіцієнта кореляції.
Властивість 1. Абсолютна величина коефіцієнта кореляції не перевищує одиниці: Властивість 2. Якщо Наслідок. Якщо коефіцієнт кореляції відмінний від нуля, то ці величини залежні Зауваження. Твердження, зворотне властивості 2, загалом кажучи, невірно, тобто рівність нулю коефіцієнта кореляції ще не свідчить про незалежність величин Властивість 3. Якщо коефіцієнт кореляції дорівнює нулю, а рівняння регресії Властивість 4. Якщо абсолютна величина коефіцієнта кореляції дорівнює одиниці, то спостережувані значення ознак зв'язані лінійною функціональною залежністю; при цьому Властивість 5. Зі зростанням абсолютної величини коефіцієнта кореляції розсіювання спостережуваних значень ознак навколо середніх зменшується, тобто лінійна кореляційна залежність стає більше тісною. Отже, коефіцієнт кореляції характеризує тісноту лінійного кореляційного зв'язку між кількісними ознаками у вибірці: чим ближче Зауваження 1. Коефіцієнт кореляції дорівнює
причому знак Зауваження 2. Для вибірки досить великого об'єму висновок про тісноту лінійної залежності між
Приклад.1. Знайти коефіцієнт кореляції по даним п = 20 спостережень, наведених у таблиці 8. Таблиця. 8
Розв’язання. Скористаємося формулами (1.6.3.) і (1.6.4). Тому що кожна пара
Маємо:
Як бачимо, коефіцієнт кореляції дуже близький до одиниці. Це означає, що розглянуті випадкові величини зв'язані практично функціональною лінійною залежністю. Приклад 2. Обчислити коефіцієнт кореляції за даними кореляційної таблиці 8 Таблиця. 8
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.78.184 (0.014 с.) |

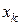 ознаки
ознаки 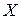 й відповідні їм значення
й відповідні їм значення 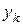 ознаки
ознаки  зустрічаються у вибірці один раз. Тоді немає необхідності говорити про умовну середню, і рівняння (1.4.1) запишеться у вигляді
зустрічаються у вибірці один раз. Тоді немає необхідності говорити про умовну середню, і рівняння (1.4.1) запишеться у вигляді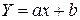 (1.4.2.1)
(1.4.2.1)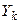 , звичайно, будуть відрізнятися від спостережуваних значень
, звичайно, будуть відрізнятися від спостережуваних значень  і
і 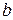 так, щоб погрішність була мінімальною. Але як це зробити? Який принцип покласти в основу мінімізації погрішності?
так, щоб погрішність була мінімальною. Але як це зробити? Який принцип покласти в основу мінімізації погрішності?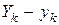 будуть, загалом кажучи, різними, а тому принцип мінімізації погрішності повинен полягати в тім, щоб сума всіх погрішностей
будуть, загалом кажучи, різними, а тому принцип мінімізації погрішності повинен полягати в тім, щоб сума всіх погрішностей 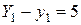 , а
, а 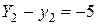 , то сумарне відхилення дорівнює нулю.
, то сумарне відхилення дорівнює нулю.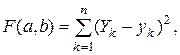
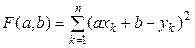 .
.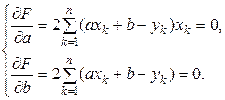 (1.4.2.2.)
(1.4.2.2.)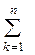 будемо писати
будемо писати 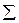 . Відповідно індекси в
. Відповідно індекси в 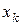 і
і 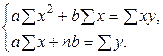 (1.4.2.3)
(1.4.2.3) . Поставивши спереду знак «
. Поставивши спереду знак « . Помноживши рівняння
. Помноживши рівняння 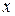 й написавши спереду знак «
й написавши спереду знак «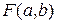 досягає найменшого значення. З геометричної точки зору це означає, що при знайдених значеннях параметрів
досягає найменшого значення. З геометричної точки зору це означає, що при знайдених значеннях параметрів  , побудовані за даними спостережень, лежать ближче до теоретичної прямої
, побудовані за даними спостережень, лежать ближче до теоретичної прямої 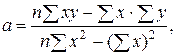 (1.4.2.4)
(1.4.2.4)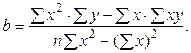 (1.4.2.5)
(1.4.2.5)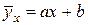
 . Очевидно, що з геометричної точки зору
. Очевидно, що з геометричної точки зору 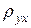 - кутовий коефіцієнт прямої лінії регресії
- кутовий коефіцієнт прямої лінії регресії 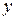 в рівнянні лінійної регресії
в рівнянні лінійної регресії 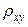 . Тому рівняння лінійної регресії
. Тому рівняння лінійної регресії  ,
,
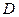 або середнє квадратическое відхилення
або середнє квадратическое відхилення 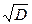 .. Вводячи поняття дисперсії в теорії ймовірностей, ми ставили задачу охарактеризувати розкид значень випадкової величини біля її математичного сподівання. Представлялося природним як таку характеристику взяти середнє значення (математичне сподівання) відхилення випадкової величини
.. Вводячи поняття дисперсії в теорії ймовірностей, ми ставили задачу охарактеризувати розкид значень випадкової величини біля її математичного сподівання. Представлялося природним як таку характеристику взяти середнє значення (математичне сподівання) відхилення випадкової величини 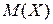 , але виявилося, що
, але виявилося, що ,
,
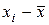 значення ознаки від загальної середньої дорівнює нулю:
значення ознаки від загальної середньої дорівнює нулю: .
. .
.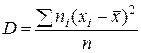 ,
, - частоти значень
- частоти значень  відповідної ознаки вибірки об'єму п.
відповідної ознаки вибірки об'єму п.
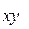

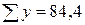
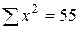
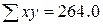
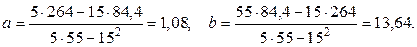
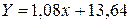 .
. -мірною випадковою величиною розуміється впорядкований набір
-мірною випадковою величиною розуміється впорядкований набір 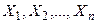 . Будемо позначати її символом
. Будемо позначати її символом 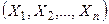 .
. . Її складові дискретні.
. Її складові дискретні.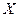 приймає значення
приймає значення  , а випадкова величина
, а випадкова величина  - значення
- значення 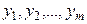 . Тоді значення випадкової величини
. Тоді значення випадкової величини 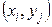
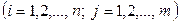 . Відповідні ймовірності
. Відповідні ймовірності 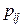 - це ймовірності того, що
- це ймовірності того, що 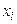 а
а 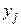 :
: 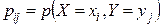 .
.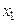

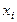


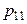
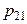



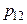
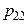
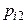

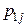
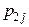
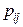
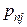
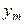
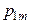
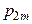


 , то сума всіх імовірностей у клітках таблиці 3 дорівнює одиниці:
, то сума всіх імовірностей у клітках таблиці 3 дорівнює одиниці: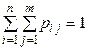 .
.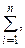 те одержимо:
те одержимо: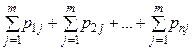 .
.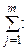
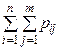
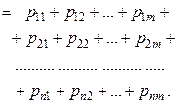
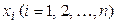 відповідає ряд розподілу величини
відповідає ряд розподілу величини 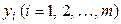 відповідає ряд розподілу величини
відповідає ряд розподілу величини 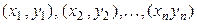
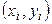 спостерігалася по одному разу. Розглянемо загальний випадок, коли конкретне значення х може зустрітися
спостерігалася по одному разу. Розглянемо загальний випадок, коли конкретне значення х може зустрітися 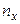 раз, конкретне значення
раз, конкретне значення 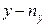 раз, а та сама пара
раз, а та сама пара 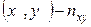 раз. Нехай
раз. Нехай 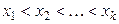 і
і 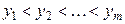 - упорядковані по зростанню різні значення
- упорядковані по зростанню різні значення 
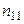

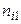


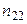
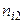
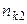
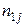
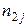
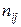
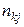
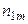
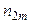
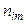
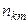
 спостережуваних пар значень
спостережуваних пар значень 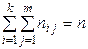 ,
, , то одержимо кореляційну таблицю відносних частот.
, то одержимо кореляційну таблицю відносних частот. .
. відповідає статистичний розподіл частот величини
відповідає статистичний розподіл частот величини 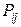 рівними відповідним відносним частотам
рівними відповідним відносним частотам 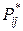 , тому що при досить більших п
, тому що при досить більших п 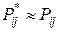 (статистична ймовірність).
(статистична ймовірність).

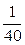
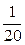
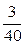
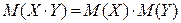
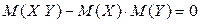 .
. , (1.6.1)
, (1.6.1) існує зв'язок. При цьому, треба думати, чим більше різниця
існує зв'язок. При цьому, треба думати, чим більше різниця  буде відрізнятися від нуля, тим тісніше зв'язок між
буде відрізнятися від нуля, тим тісніше зв'язок між  , що визначається формулою
, що визначається формулою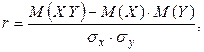 (1.6.2)
(1.6.2) – середнє квадратическое відхилення величини
– середнє квадратическое відхилення величини 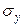 – середнє квадратическое відхилення величини
– середнє квадратическое відхилення величини  .
. . (1.6.3)
. (1.6.3)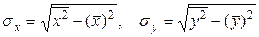 . (1.6.4)
. (1.6.4)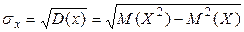 .
.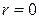 .
.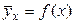 й
й 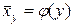 линійні, то
линійні, то  у випадку прямого зв'язку і
у випадку прямого зв'язку і 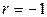 у випадку зворотного зв'язку.
у випадку зворотного зв'язку.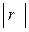 до нуля, тим цей зв'язок слабкіше, а у випадку
до нуля, тим цей зв'язок слабкіше, а у випадку 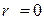 лінійний кореляційний зв'язок відсутній. Чим ближче
лінійний кореляційний зв'язок відсутній. Чим ближче 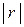 до одиниці, тим лінійний зв'язок сильніше, переходячи у випадку
до одиниці, тим лінійний зв'язок сильніше, переходячи у випадку  у функціональний.
у функціональний. ,
,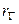 нормально розподіленої генеральної сукупності за коефіцієнтом кореляції
нормально розподіленої генеральної сукупності за коефіцієнтом кореляції 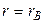 вибірки може бути зроблена (при
вибірки може бути зроблена (при  )по формулі
)по формулі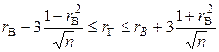 .
.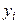
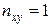 . Підрахуємо всі складові цих формул.
. Підрахуємо всі складові цих формул.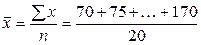 = 121,8.
= 121,8.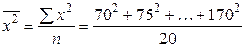 = 15728,5.
= 15728,5.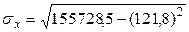 = 29,89.
= 29,89.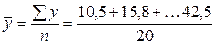 = 28,63.
= 28,63.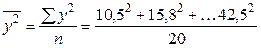 = 907,98.
= 907,98.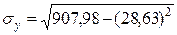 = 9,4.
= 9,4.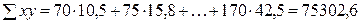 .
.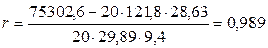 .
.



