
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Відшукання параметрів рівняння лінійної регресії за згрупованим данимиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
У п.1.4. для знаходження параметрів а і
Передбачалося, що значення Зі співвідношень
випливає, що
Тому що пара чисел
Позначимо, як було сказано раніше,
(У другому рівнянні системи зроблене скорочення на п) Возв’язавши цю систему, знайдемо
Нескладно довести, що в це рівняння лінійної регресії
де Використовувати рівняння (1.8.3) простіше, ніж утворювати і розв’язувати систему (1.8.2), а потім знаходити коефіцієнт кореляції для встановлення тісноти кореляційного зв'язку.
Зауваження 1. Аналогічно знаходять рівняння лінійної регресії
де Зауваження 2. Рівняння (1.8.3) і (1.8.4) можна записати в більше симетричній формі:
Приклад. Знайти лінійне рівняння регресії
Розв’язання. У прикладі попереднього пункту 1.7. уже обчислені
Формули (1.8.5) і (1.8.6)випливають із формул (1.7.1)
Обчислимо
Підставимо ці величини і коефіцієнт кореляції, що знайдений раніше (
Одержимо шукане рівняння
або
Перевірка гіпотези про значущість коефіцієнта Кореляції
Приведемо деякі визначення. Статистичною називають гіпотезу (припущення) про вид невідомого розподілу або про параметри відомих розподілів. Висунуту гіпотезу Конкуруючою (альтернативною) гіпотезою називають гіпотезу Висунута гіпотеза Помилка першого роду полягає в тому, що може бути відкинута правильна гіпотеза. Помилка другого роду полягає в тому, що буде прийнята неправильна гіпотеза. Наслідки цих помилок можуть бути самими різними. Наприклад, якщо відкинуто правильне рішення «продовжувати будівництво житлового будинку», те ця помилка першого роду спричинить матеріальний збиток. Якщо ж прийняти неправильне рішення «продовжувати будівництво», то ця помилка другого роду може спричинити різні наслідки (обвал будинку і т.д.). Ймовірність зробити помилку першого роду називають рівнем значущості. Природно, що ця ймовірність повинна бути дуже малої. Найбільш уживані рівні значимості 0,05; 0,002;0,01, рідше 0,10 або 0,001. Щоб краще «відчути» рівень значимості, можна скористатися аналогією між ймовірністю і частотою. Якщо, наприклад, прийнятий рівень значущості 0,05. те це означає, що в середньому в п'яти випадках з 100 ми ризикуємо припуститися помилки першого роду (відкинути правильну гіпотезу). Для перевірки нульової гіпотези використовують спеціально підібрану випадкову величину К, точний або наближений розподіл якої відомий. Її називають статистичним критерієм (або просто критерієм). Критичною областю називають множина значень критерію К, при яких нульова гіпотеза відкидається. Областю прийняття гіпотези називають множина значень критерію К, при яких гіпотеза приймається. Критичними точками Якщо критична область визначається нерівністю Лівосторонньою називають критичну область, де Правосторонню або лівосторонню критичну область називають односторонньою. Двосторонньою критичною областю називають критичну область, яка визначається нерівностями Зауваження У випадку прийняття нульової гіпотези не слід думати, що вона доведена. Дійсно, одиничний приклад, що підтверджує яке-небудь твердження, ще не доводить його. Тому більш правильно говорити, що дані спостережень погодяться з нульовою гіпотезою, а тому немає підстав її відкинути. Для більшої впевненості прийняття гіпотези можна перевірити її іншими способами або збільшити число спостережень. Якщо спостережуване значення критерію належить критичній області, то це суперечить нульовій гіпотезі, що дозволяє її відхилити. Дійсно, одиничний приклад, що суперечить деякому загальному твердженню, дозволяє його відхилити. На практиці, якщо спостережуване значення статистичного критерію належить критичній області, гіпотезу відкидають, а якщо спостережуване значення ознаки належать області прийняття гіпотези, гіпотезу приймають у тому розумінні, що немає підстав її відкинути. Покажемо, як здійснюється перевірка гіпотези про значущість вибіркового коефіцієнта кореляції. Нехай двовимірна генеральна сукупність ( Як критерій нульової гіпотези приймають випадкову величину
Ця величина при справедливості нульової гіпотези має розподіл Стьюдента ( У випадку діаметрально протилежних нульової й конкуруючої гіпотез (у цьому випадку Перевірка нульової гіпотези при заданому рівні 1. За даними спостережень обчислюють спостережуване значення критерію
2. По таблиці критичних точок розподілу Стьюдента (додаток 1) по заданому рівні значущості Якщо Якщо
Приклад. З вибірки об'єму Розв’язання. Знайдемо спостережуване значення критерію:
По таблиці критичних точок розподілу Стьюдента для двосторонньої області за рівнем значущості
Питання й задачі для самоперевірки 1. Який зв'язок між випадковими величинами 2. Який зв'язок між випадковими величинами 3. Нехай між 4. Нехай 5. Сформулюйте дві основні задачі теорії кореляції. 6. 7. Яка ідея методу найменших квадратів? 8. Проведіть аналогію між визначеннями дисперсії
у теорії ймовірностей і в математичній статистиці:
де значення ознаки вибірки об'єму п 9. Що називається кореляційною таблицею? 10. Яка ідея визначення коефіцієнта кореляції по формулі
11. Перелічите властивості коефіцієнта кореляції. 12. Чи можна сказати, що коефіцієнт кореляції характеризує тісноту кореляційного зв'язку? 13. Що розуміють під: а) рівнем значущості статистичної гіпотези? б) нульовою й конкуруючою гіпотезами? в) статистичним критерієм? г) критичною областю? д) областю прийняття рішень? е) критичною точкою? 14. Чи приймається нульова гіпотеза, якщо спостережуване значення критерію належить критичній області? 15. Чи приймається нульова гіпотеза, якщо спостережуване значення критерію належить області прийняття гіпотези? Чи свідчить цей факт про те, що нульова гіпотеза доведена. Задача. Знайти рівняння лінійної регресії Таблиця 17
Відповідь. 1.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.108 (0.008 с.) |

 лінійного рівняння регресії
лінійного рівняння регресії  за незгрупованим даними була одержана нормальна система
за незгрупованим даними була одержана нормальна система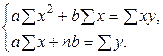 (1.8.1)
(1.8.1)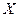 і відповідні їм значення
і відповідні їм значення  спостерігалися по один раз. При великій кількості статистичних даних, як правило, серед пар значень
спостерігалися по один раз. При великій кількості статистичних даних, як правило, серед пар значень  є повторювані. Тоді їх групують і утворюють кореляційну таблицю (див.п.1.5). Запишемо систему (1.8.1) так, щоб вона відбивала дані кореляційної таблиці.
є повторювані. Тоді їх групують і утворюють кореляційну таблицю (див.п.1.5). Запишемо систему (1.8.1) так, щоб вона відбивала дані кореляційної таблиці.
 .
. спостерігалася
спостерігалася  раз, то
раз, то .
. . Тоді система (1.8.1) прийме наступний вид:
. Тоді система (1.8.1) прийме наступний вид: (1.8.2)
(1.8.2) і
і  .
. , (1.8.3)
, (1.8.3) =
=  :
: , (1.8.4)
, (1.8.4) =
= 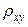 .
. ,
, .
. . Тепер
. Тепер  і
і 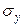 можна знайти по наступних формулах:
можна знайти по наступних формулах: ,
,  , (1.8.5)
, (1.8.5)
 . (1.8.6)
. (1.8.6) :
: ,
, ,
, =
=  ,
, .
. ), у рівняння лінійної регресії
), у рівняння лінійної регресії ,
, ,
, .
. називають нульовою (основною).
називають нульовою (основною). , що суперечить нульовій.
, що суперечить нульовій. може бути правильною або неправильною, тому виникає необхідність її перевірки. У результаті такої перевірки методами математичної статистики можуть бути допущені помилки двох родів.
може бути правильною або неправильною, тому виникає необхідність її перевірки. У результаті такої перевірки методами математичної статистики можуть бути допущені помилки двох родів. називають точки, що відокремлюютькритичну область від області прийняття рішень. Їх знаходять по спеціальних таблицях.
називають точки, що відокремлюютькритичну область від області прийняття рішень. Їх знаходять по спеціальних таблицях. (
( ), то її називають правосторонньою.
), то її називають правосторонньою. (
( ).
). , де
, де  . Зокрема, якщо критичні точки симетричні щодо нуля, двостороння критична область визначається нерівністю
. Зокрема, якщо критичні точки симетричні щодо нуля, двостороння критична область визначається нерівністю  , якщо
, якщо 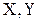 ) має нормальний розподіл. З її зроблена вибірка об'єму п і по цій вибірці знайдений вибірковий коефіцієнт кореляції
) має нормальний розподіл. З її зроблена вибірка об'єму п і по цій вибірці знайдений вибірковий коефіцієнт кореляції  , що виявився відмінним від нуля. Тому що вибірка зроблена випадково, то ми не можемо бути впевнені, що коефіцієнт кореляції генеральної сукупності (генеральний коефіцієнт кореляції) також не дорівнює нулю. Ставиться задача: при заданому рівні значущості
, що виявився відмінним від нуля. Тому що вибірка зроблена випадково, то ми не можемо бути впевнені, що коефіцієнт кореляції генеральної сукупності (генеральний коефіцієнт кореляції) також не дорівнює нулю. Ставиться задача: при заданому рівні значущості  перевірити нульову гіпотезу
перевірити нульову гіпотезу  при конкуруючій гіпотезі
при конкуруючій гіпотезі  .
. .
. - розподіл) зі
- розподіл) зі  ступенями свободи.
ступенями свободи. ) будують двосторонню критичну область.
) будують двосторонню критичну область.
 для двосторонньої критичної області
для двосторонньої критичної області ,то немає підстав відкинути нульову гіпотезу.
,то немає підстав відкинути нульову гіпотезу. ,то нульову гіпотезу відкидають. Це означає, що вибірковий коефіцієнт кореляції є значущим, тобто він невипадково відрізняється від нуля. У свою чергу, це означає, що величини
,то нульову гіпотезу відкидають. Це означає, що вибірковий коефіцієнт кореляції є значущим, тобто він невипадково відрізняється від нуля. У свою чергу, це означає, що величини 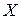 і
і  зв'язані лінійною кореляційною залежністю.
зв'язані лінійною кореляційною залежністю. , витягнутої із двовимірної нормальної генеральної сукупності (
, витягнутої із двовимірної нормальної генеральної сукупності ( . Потрібно на рівні значущості
. Потрібно на рівні значущості  перевірити нульову гіпотезу про рівність нулю генерального коефіцієнта кореляції при конкуруючій гіпотезі
перевірити нульову гіпотезу про рівність нулю генерального коефіцієнта кореляції при конкуруючій гіпотезі  .
.
 знаходимо критичну точку. Вона перебуває між 1,98 і 2,00. Тому що
знаходимо критичну точку. Вона перебуває між 1,98 і 2,00. Тому що  > tкр, те гіпотеза про рівність нулю генерального коефіцієнта кореляції відкидається. Інакше кажучи,
> tкр, те гіпотеза про рівність нулю генерального коефіцієнта кореляції відкидається. Інакше кажучи,  зв'язані кореляційною залежністю.
зв'язані кореляційною залежністю. називається статистичним?
називається статистичним?
 ,
, мають відповідно частоти
мають відповідно частоти  причому
причому  .
. ?
? при конкуруючій гіпотезі
при конкуруючій гіпотезі 
 ; 2.
; 2.  ; 3.
; 3.  .
.  >
>  . Гіпотеза про рівність нулю
. Гіпотеза про рівність нулю 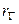 відкидається.
відкидається.


