
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перевірка гіпотез про коефіцієнт нахилу регресіїСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Стандартною процедурою є перевірка гіпотези про те, що коефіцієнт нахилу регресійної прямої b дорівнює нулю. Прийняття цієї гіпотези означає, що незалежна змінна не має впливу на залежну в рамках лінійної моделі. Не виключено, що насправді між змінними існує залежність, але виражена іншою функціональною формою. Статистика для перевірки гіпотези має вигляд
Значення цієї t -статистики, як правило, автоматично підрахо-вуються в комп’ютерних програмах з регресійного аналізу. Для перевірки гіпотези
За вибраним рівнем значущості a в таблиці розподілу Стьюдента з n- 2 ступенями свободи знаходимо критичне значення t кр. Якщо Інтервальне оцінювання Інтервальна оцінка параметра b з рівнем довіри 1-a (не плутати з постійним доданком у регресії) знаходиться за наступною формулою:
де значення t кр знаходиться за вибраним a в таблиці розподілу Стьюдента з n- 2 ступенями свободи. Перевірка значущості регресії Значущість регресії означає, що незалежні змінні впливають на залежну змінну. Для простої лінійної регресіі це еквівалентно тому, що коефіцієнт нахилу не дорівнює нулю (тобто коли гіпотеза про рівність b нулю відхиляється). Якщо b = 0, то
коли b = 0, де через F 1, n– 2 позначено розподіл Фішера з 1, n– 2 ступенями свободи. За вибраним рівнем значущості a в таблиці розподілу Фішера з 1, n- 2 ступенями свободи знаходимо критичне значення F кр. Якщо | F |< F кр, то гіпотеза приймається. Якщо | F |³ F кр, то гіпотеза відхиляється. У випадку простої регресії застосування F -критерія (1.23) не дає нової інформації порівняно з t -критерієм (1.20), оскільки
1.1.7. Прогнозування за допомогою простої лінійної регресії Припустимо, ми хочемо одержати інформацію про можливі значення залежної змінної y 0за умови, що незалежна змінна x приймає деяке значення x 0. Внаслідок (1.1)
Оскільки E a = a іE b = b, то
Для того, щоб (1.25) можна було б використовувати для інтервального оцінювання залишилось замінити дисперсію збурень на її оцінку. Позначимо
стандартна похибка прогнозу. Інтервальний прогноз з рівнем довіри 1-a знаходиться за наступною формулою:
де
Приклад В Таблиці 1.1. наведено обсяги сукупного доходу у розпорядженні та сукупного споживання для США у постійних доларах 1972 р. Дані з Таблиці 1.1. зображено графічно на на Рис.1.3. З графіка видно, що точки, які відповідають спостереженням, розташовані навколо деякої прямої, отже доцільно розглянути лінійну функцію споживання. Оцінимо її за допомогою моделі простої лінійної регресії: yi = a + b xi + e i, де через xi та yi позначено відповідно рівень доходу і споживання в році 1969 + i (наприклад i = 5 відповідає 1974 року). Спочатку обчислимо Таблиця 1.1.
Рис. 1.3.
= 879,24;
= 793,43;
Sxx = ((751,6 – 879,24)2 + (779,2 – 879,24)2 + (810,3 – 879,24)2 + + (864,7 – 879,24)2 + (857,5 – 879,24)2 + (874,9 – 879,24)2 + + (906,8 – 879,24)2 + (942,9 – 879,24)2 + (988,8 – 879,24)2 + + (1015,7879,24)2) = 67192,4;
Syy = ((672,1 – 793,43)2 + (696,8 – 793,43)2 + (737,1 – 793,43)2 + + (767,9 – 793,43)2 + (762,8 – 793,43)2 + (779,4 – 793,43)2 + + (823,1 – 793,43)2 + (864,3 – 793,43)2 + (903,2 – 793,43)2 + + (927,6 – 793,43)2) = 64972,1;
Sxy = ((751,6 – 879,24) (672,1 – 793,43) + (779,2 – 879,24) (696,8 – 793,43) + + (810,3 – 879,24) (737,1 – 793,43) + (864,7 – 879,24) (767,9 – 793,43) + + (857,5 – 879,24) (762,8 – 793,43) + (874,9 – 879,24) (779,4 – 793,43) + + (906,8 – 879,24) (823,1 – 793,43) + (942,9 – 879,24) (864,3 – 793,43) + +(988,8 – 879,24) (903,2 – 793,43) + (1015,7879,24) (927,6 – 793,43)) = = 65799,3. За формулами (1.7) знаходими оцінки методу найменших квадратів коефіцієнгів моделі (1.27):
Отже, рівняння вибіркової регресійної прямої (рівняння фунцції споживання) має вигляд:
= 0.979´65799,3/64972,1 = 0.990702.
Як ми бачимо, зв’язок між споживанням і доходом є вельми тісним. Перед тим, як використовувати рівняння (1.28) для економічного аналізу або побудови прогнозів, модель (1.27) потрібно перевірити на адекватність. Перевіримо гіпотезу про значущість регресії двома способами. Спочатку використаємо F -статистику (1.23):
Нехай, рівень значущості a дорівнює 0,05. В Таблиці 3. Додатку знаходимо, що критичне значення F кр = 5,32. Ми бачимо, що | F |³ F кр, отже гіпотеза про рівність b нулю відхиляється, тим самим модель (1.27) є значущою. Обчислимо стандартні похибки оцінок. Спочатку знайдемо суму квадратів залишків RSS. За формулою (1.15) RSS = Syy – b 2 Sxx = 64972,1 – 0.9792´67192,4 = 537,0. Далі знаходимо оцінку дисперсії збурень
стандартна похибка b дорювнює:
SE( b) =
Перевіримо гіпотезу про те, що коефіцієнт нахилу регресійної прямої b дорівнює нулю за допомогою t -статистики (1.20):
Нехай, рівень значущості a дорівнює 0,05. В Таблиці 1. Додатку знаходимо, що критичне значення t кр = 2,306. Ми бачимо, що | t |³ t кр, отже гіпотеза відхиляється. Отже, ми можемо вважати модель адекватною (читач не повинен забувати, що повна перевірка моделі на адекватність включає аналіз залишків, з елементами якого ми ознайомимось в розділах 3 та 4). З теорії споживання відомо, що коефіцієнт нахилу лінійної функції споживання є маргінальною або граничною схильністю до споживоння. Таким чином, ми встановили, що в середньому 0.979 ´ 100 = 97,9% прирісту доходу витрачається на споживання1). Обчислене значення граничної схильності до споживання знаходиться в інтервалі (0; 1), що узгоджується з економічною теорією. Множинна лінійна регресія 1.2.1. Опис моделі За допомогою моделі простої лінійної регресіїї ми вивчали зв’язок між залежною змінною y та незалежною змінною x. Модель множинної лінійної регресії описує співвідношення між y та набором незалежних змінних x0, x 1,..., xk -1. Так, наприклад, при дослідженні попиту нас цікавить залежність обсягу попиту на деякий товар від ціни на цей товар, цін на взаємозамінні з даним товари та від доходів споживачів. При наявності n спостережень модель множинної лінійної регресії записується у вигляді
де xij – значення j -ї незалежної змінної (xj) в i -му спостереженні, збурення e i задовольняють тим самим припущенням, що і в моделі простої регресії. 1. Нульове середнє: E e i = 0, 2. Рівність дисперсій: De i = E 3. Незалежність збурень: e і та e j незалежні при 4. Незалежність збурень та регресорів: xij та e і незалежні для всіх i та j (якщо регресори не стохастичні, то дане припущення виконується автоматично). 5. (Додаткове). Збурення e i нормально розподілені для всіх i. Модель множинної лінійної регресії (1.29) зручно записувати у матрично-векторному вигляді:
з використанням наступних позначень:
Матриця X складається з n рядків – відповідно до кількості спостережень, – і з k стовпчиків, кількість яких дорівнює кількості незалежних змінних. Щоб записати модель з константою:
у матричному вигляді, розглядають матрицю значень незалежних змінних, в якій перший стовпчик складається з одиниць:
Позначимо через D e коваріаційну матрицю вектора збурень
внаслідок того, що збурення мають нульові математичні сподівання. Тоді припущення 2 та 3 зручно записувати у вигляді: De =s2 I n, (1.31) де I n – одинична матриця n -го порядку, а припущення 1 – E e = 0. Модель множинної лінійної регресії у матрично-векторних позначеннях:
e не залежить від X Додаткове припущення: e ~ N (0,s2 I)
1.2.2. Знаходження параметрів регресії методом найменших квадратів Нехай
Тоді
є оцінкою E yi, побудованою на основі вибіркової регресіїї. Залишки
Вектор залишків Оцінки методу найменших квадратів знаходяться з умови мінімізації суми квадратів залишків за всіма можливими значеннями
Щоб мінімізувати вираз (1.32), запишемо необхідну умову екстремуму, тобто прирівняємо похідні відносно
тобто, система нормальних рівнянь має вигляд
звідки
Перевірка достатніх умов екстремуму показує, що
Оцінка методу найменших квадратів коефіцієнтів моделі моделі множинної лінійної регресії знаходиться за формулою:
Рівняння вибіркої регресії приймає вигляд
або, у випадку регресії з костантою,
Рівняння вибіркої регресії є рівнянням лінійної функції багатьох змінних.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 714; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.104.244 (0.007 с.) |

 (1.20)
(1.20) H0: b = b0 використовують наступну статистику
H0: b = b0 використовують наступну статистику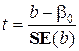 (1.21)
(1.21) , (1.22)
, (1.22) = 0. Тому логічно будувати критерій, який грунтується на значенні коефіцієнта детермінації. Дійсно, можна показати, що
= 0. Тому логічно будувати критерій, який грунтується на значенні коефіцієнта детермінації. Дійсно, можна показати, що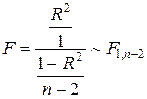 (1.23)
(1.23) і
і  . Але це не так у випадку множинної регресії, що ми побачимо пізніше.
. Але це не так у випадку множинної регресії, що ми побачимо пізніше. . Точковий прогноз знаходиться за формулою
. Точковий прогноз знаходиться за формулою (1.24).
(1.24). . Отже, прогноз (1.24) є незміщеним. Дисперсія
. Отже, прогноз (1.24) є незміщеним. Дисперсія  прогнозу (1.24) дорівнює
прогнозу (1.24) дорівнює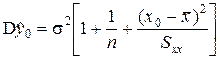 (1.25).
(1.25). – (1.26)
– (1.26) ,
, – точковий прогноз (1.24), а значення t кр знаходиться за вибраним a в таблиці розподілу Стьюдента з n- 2 ступенями свободи.
– точковий прогноз (1.24), а значення t кр знаходиться за вибраним a в таблиці розподілу Стьюдента з n- 2 ступенями свободи. , (1.27)
, (1.27)
 =(751,6+779,2+810,3+864,7+857,5+874,9+906,8+942,9+988,8+1015,7)/10 =
=(751,6+779,2+810,3+864,7+857,5+874,9+906,8+942,9+988,8+1015,7)/10 = =(672,1+696,8+737,1+767,9+762,8+779,4+823,1+864,3+903,2+927,6)/10 =
=(672,1+696,8+737,1+767,9+762,8+779,4+823,1+864,3+903,2+927,6)/10 =
 = – 67,58 + 0.979 x. (1.28)
= – 67,58 + 0.979 x. (1.28) Рис 1.4
Рис 1.4
 .
. .
. 0.0316071.
0.0316071. .
. (1.29)
(1.29) .
. = s2 = const,
= s2 = const,  .
. (1.30)
(1.30) –вектор значень залежної змінної,
–вектор значень залежної змінної, – матриця значень незалежних змінних,
– матриця значень незалежних змінних, – вектор збурень,
– вектор збурень, – вектор параметрів (коефіцієнтів) регресії.
– вектор параметрів (коефіцієнтів) регресії.
 .
.
 ,
,
 –деяка оцінка вектора параметрів
–деяка оцінка вектора параметрів  . Запишемо рівняння вибіркої регресії
. Запишемо рівняння вибіркої регресії .
.
 визначаються як різниці між значеннями залежної змінної, які спостерігались, і обчисленими з регресії:
визначаються як різниці між значеннями залежної змінної, які спостерігались, і обчисленими з регресії: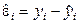 .
. дорівнює
дорівнює  , де
, де  ,
,  .
.
 (1.32)
(1.32) до нуля. Маємо
до нуля. Маємо ,
, ,
, . (1.33)
. (1.33) .
. (1.34)
(1.34) . (1.35),
. (1.35), (1.36).
(1.36).


