
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Автокореляція внаслідок неправильно визначеної динаміки.Содержание книги
Поиск на нашем сайте
Інша можливість – це автокореляція внаслідок неправильно визначеної динаміки. Така ситуація виникає, коли реакція залежної змінної на зміни незалежних змінних не є миттєвою, а розповсюджена в часі. Якщо відсутні специфічні міркування щодо характеру такої реакції найбільш доцільним шляхом є розгляд моделі з авторегресійно розподіленими лагами
замість звичайної моделі
В моделі
1.5.9.2. Критерій множників Лагранжа Бройша–Годфрі За допомогою критерію множинників Лагранжа перевіряють гіпотезу
де Т-кількість спостережень, асимптотично має розподіл
Звичайний метод найменших квадратів Для оцінювання моделей з автокорельованими збуреннями можна використати звичайний метод найменших квадратів: як-зазначалося вище, проблеми існують скоріше не з оцінками параметрів (хоча вони і не будуть оптимальними), а зі стандартною оцінкою коваріаційної матриці. Неві та Вест запропонували наступну оцінку, яка є консистентною в досить широких умовах стосовно природи автокореляції
Корельованість збурень в моделях з просторовими даними. Істотна відмінність між просторовими даними і часовими рядами полягає в тому, що в останньому випадку існує єдиний природний спосіб сортування виборки- сортування за часом, тоді ж як ситуації зі структурними даними сортування виборки може бути, взагалі кажучи, довільним. Внаслідок цього значення статистики Дуррбіна-Уотсона може визначатись просто способом сортування виборки. Якщо дані є просторовими не має сенсу розглядати збурення як випадковий процес або казати про неправильно визначеу динаміку. Проте, в тому випадку, коли спостереження відсортовані за певною логікою, корельованість залишків може свідчити про проблеми з моделлю- неправильно визначену функціональну форму або пропущені змінні. В такій ситуації можна опинитись якщо дані відсортовані в порядку зростання залежної змінної. Якщо дані відсортовані географічним принципом, корельованість залишків може свідчити про відсутність змінних, які характеризують регіональні відмінності. Цю проблему можна розв’язати шляхом включення до моделі фіктивних змінних. Метод максимальної правдоподібності.
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.214.184 (0.007 с.) |



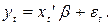
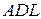 слід перевірити гіпотези
слід перевірити гіпотези 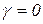 і
і 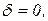 а також перевірити її на наявність автокореляції. Слід пам’ятати, що внаслідок корельованості
а також перевірити її на наявність автокореляції. Слід пам’ятати, що внаслідок корельованості 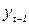 з
з  МНК-оцінки, хоча і зберігають властивість консистентності, будуть зміщеними. Отже, всі стандартні результати вірні лише асимптотично. Крім того, внаслідок наявності лагового значення залежної змінної
МНК-оцінки, хоча і зберігають властивість консистентності, будуть зміщеними. Отже, всі стандартні результати вірні лише асимптотично. Крім того, внаслідок наявності лагового значення залежної змінної 
 автокореляція відсутня протии.
автокореляція відсутня протии. 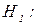 збурення утворюють процес
збурення утворюють процес 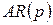 або
або 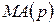 , тобто має місце автокореляція порядку
, тобто має місце автокореляція порядку 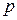 . Для обчислення LM-статистики потрібно оцінити допоміжну регресію залишків звичайного методу найменших квадратів
. Для обчислення LM-статистики потрібно оцінити допоміжну регресію залишків звичайного методу найменших квадратів 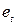 відносно
відносно 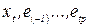 (заповняючи пропущені значення -лагових залишків нулями). Нехай
(заповняючи пропущені значення -лагових залишків нулями). Нехай 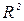 - коєфіцієнт детермінації в цій регресії. В припущенні, що нульова гіпотеза вірна, статистика
- коєфіцієнт детермінації в цій регресії. В припущенні, що нульова гіпотеза вірна, статистика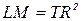 ,
, -квадрат з p степенями свободи. Зауважимо, що при
-квадрат з p степенями свободи. Зауважимо, що при 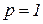 даний критерій може використовуватись як альтернатива критерію Дурбіна-Ватсона, навіть в ситуаціях коли останній можна застосовувати.
даний критерій може використовуватись як альтернатива критерію Дурбіна-Ватсона, навіть в ситуаціях коли останній можна застосовувати. де
де 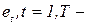 залишки звичайного методу найменших квадратів,
залишки звичайного методу найменших квадратів, 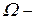 діагональна матриця з.t-м діагональним елементом, рівним
діагональна матриця з.t-м діагональним елементом, рівним 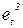 ,
,  -вектор значень регресорів в.t-му спостереженні,
-вектор значень регресорів в.t-му спостереженні, 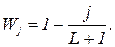 Константа
Константа  визначається таким порядком автокореляції, що автокореляцією вищих порядків можна знехтувати. Тобто, наприклад, якщо збурення генеруються процесом-
визначається таким порядком автокореляції, що автокореляцією вищих порядків можна знехтувати. Тобто, наприклад, якщо збурення генеруються процесом- 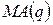 , то L=q. У випадку авторегресійних збурень визначена
, то L=q. У випадку авторегресійних збурень визначена 


