
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Звичайний метод найменших квадратівСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для оцінювання моделей з гетероседистичними збуреннями можна використати звичайний метод найменших квадратів. Консистентну у випадку гетероседистичності оцінку коваріаційної матриці було запропоновано Уайтом
де Єдиною додатковою умовою для консистентності і асимптотичної нормальності у порівнянні з класичною моделлю є умова обмеженості всіх Оцінки доступного зваженого МНК будуть асимптотично еквівалентними оцінкам ЗвМНК у видку відомих вагів лише у випадку наявності консистентних оцінок останніх. Ця умова є також необхідною для коректності оцінювання коваріаційної матриці (звичайно, в асимптотичному розумінні; про можливість точного оцінювання взагалі мова не йде). Отже, у випадку, коли дослідник не впевнений у характеру гетероскедастичності, перевагу слід віддати звичайному методу найменших квадратів. Перевірка гіпотез здійснюється звичайним чином, але у відповідних формулах стандартну оцінку слід замінити на оцінку (1.92).
1.5. Модель лінійної регресій з автокорельованими збуреннями 1.5.1. Вступ В цьому розділі ми розглянемо регресійні моделі, в яких порушується припущення 3 – про незалежність збурень. Є дві ситуації, в яких збурення в моделях лінійної регресії можуть бути корельованими. Припустимо, ми розглядаємо модель, яка вивчає особисте споживання. Тодi логiчно очiкувати, що для домогосподарств, які розташовані недалеко одне вiд одного, у структурi споживання спостерiгатиметься бiльше подібності. І, якщо даний еффект не враховано в моделі, він впливатиме на характер збурень – вони будуть корельованими. Кореляція, що виникає у подібних випадках, має назву спатіальної, або просторової, кореляції. В деяких випадках проблему спатіальної кореляції можна розв’язати за допомогою фіктивних змінних. Автокореляцiя, або часова кореляцiя збурень виникає у моделях, побудованих за даними, якi є часовими рядами. Такий тип кореляцiї збурень пов`язаний з тим, що деякi економiчнi системи мають, так би мовити, інерцiю, тобто якщо в деякий момент часу за певних причин виникло вiдхилення вiд закономiрної поведiнки (нагадаємо, що збурення і відтворюють в моделі такі відхилення), то вплив вiд цього може спостерiгатись на протязi декiлькох наступних перiодiв часу. Нехай, наприклад, ми вивчаємо рiвень безробiття за допомогою деякої моделi. У деякий момент часу фактичний рівень безробiття був бiльшим, нiж розрахований з моделi. Оскiльки для того, щоб зменшити рiвень безробiття потрiбен час, то логiчно очiкувати, що i наступний фактичний рiвень безробiття також буде бiльшим, нiж теоретичний. Якщо згадати інтерпретацію збурень, то стане зрозуміло, що останні міркування суперечать припущенню про некорельованість збурень. Надалі в цьому розділі ми розглядатимемо саме проблему автокореляціі.
1.5.2. Опис моделi Спочатку домовимось про термінологію. Як і в попередньому розділі літерою u позначимо вектор збурень у вихідній моделі, а літеру e зарезервуємо для позначення некорельованих і гомоскедастичних збурень. Розглянемо модель лінійної регресії
в якій вектор збурень u = (u1, u2... u n)T має такi властивостi: 1. 2. Рівність дисперсій: Du i = 3. Корельованість: 4. Незалежність збурень та регресорів: xij та u і незалежні для всіх i та j. 5. (Додаткове) Збурення u i нормально розподілені для всіх i. Припущення 2 і 3 зручно записувати у матричному вигляді: D u = s2 S, (1.95) де s2>0 – спільне значення дисперсії збурень, S – додатньо визначена недiагональна матриця, на головній діагоналі якої стоять одиниці, матриця S є кореляційною матрицею збурень. Зауваження. Останнім часом також вивчаються моделі, побудовані за так званими панельними даними, збурення в яких водночас гетероскедастичні і корельовані. Такі моделі буде роглянуто в третьому розділі. 1.5.3.Наслiдки автокорельованостi збурень на оцiнки методу найменших квадратiв 1.Оцiнки МНК будуть незмiщеними, але не будуть ефективними (не матимуть найменшої дисперсiї). 2.Стандартнi оцiнки коварiацiйної матрицi оцiнки МНК будуть змiщеними, i, як наслiдок, процедури перевiрки гiпотез та iнтервального оцiнювання, основанi на стандартних статистиках, будуть некоректними.
1.5.4. Узагальнений метод найменших квадратiв у випадку відомої кореляційної матриці Припустимо, що матриця S вiдома. Оскiльки вона додатньо визначена, то для неї iснує матриця Введемо наступні позначення:
Домножимо рiвнiсть (1.93) зліва на матрицю
Зазначимо, що вектори коефiцiентiв b в моделях (1.94) i (1.96) спiвпадають. Знайдемо коварiацiйну матрицю збурень e в моделi (1.96). Спочатку обчислимо математичне сподiвання:
Отже,
Ми скористались тим, що Означення. Оцiнкою узагальненого МНК коефiцiєнтiв моделi (1.94) називається оцінка звичайного МНК, знайдена за моделлю (1.96). Зауваження. Якщо матриця S є дiагональною, то узагальнений МНК в точностi спiвпадає зi зваженим МНК. На практицi у бiльшостi випадкiв матриця S є невiдомою. Якщо не робити нiяких додаткових припущень щодо структури матрицi S, то її оцiнити неможливо, оскiльки при наявностi n спостеpежень ця матриця мiстить
1.5.5. Процес авторегресiї першого порядку Нехай задана стаціонарна послiдовнiсть випадкових величин (u i, i =0, u i = ru i -1+ e i, (1.98) де r–чисельний параметр, а e i задовольняють тим самим припущенням, що і збурення в класичній лінійній регресії, тобто Ee i = 0, (1.99) De i = s 2 = const, (1.100) cov(e i, e j) = Ee i e j = 0, cov(e i,u j) = 0, Стаціонарність послідовності (1.98) означає, що Eu i = 0, (1.103) Du i = const, (1.104) cov(u i, u i -k) = cov(u i+m, u i+m -k) (1.105) для будь-яких m та k. Іншими словами коваріація між u i та u j не залежить від i та j, а залежить лише від їх різниці. Послідовність (1.98) називається процесом авторегресiї першого порядку, позначення–AR(1). Величина cov(u i, u i -k) називається коваріацією k-го порядку процесу. Обчислимо дисперсію та коваріації процесу AR(1). Для знаходження дисперсії скористаємось формулою (1.98):
внаслідок (1.102) і (1.104). З формули (1.06) маємо
З виразу (1.107) бачимо, що стаціонарний процес з властивостями (1.99)-(1.102) існує, коли
внаслідок (1.102), (1.104) та (1.107). Виразимо коваріацію k- го порядку через коваріацію k –1 - го порядку. Для цього домножимо рівність (1.98) почленно на u i - k і обчислимо математичне сподівання обох частин
внаслідок (1.102) та (1.105). Рекурентною підстановкою (1.109), враховуючи (1.108), одержуємо
Формули (1.107) і (1.110) показують, що дисперсія та коваріації процесу авторегресії першого порядку визначаються лише двома параметрами – r та s2. 1.5.6. Узагальнений метод найменших квадратiв у випадку AR(1)-збурень Нехай в моделі (1.94) збурення підпорядковані процесу авторегресіїї першого порядку. Це означає, що збурення u i,
Результати множення рiвності (4.1) на матрицю
Елементи j- го (
Якщо у вихідній моделі є постійний доданок, то перетворена модель не матиме константи. Замість неї з’явиться змінна
Зауважимо, що оцінка
1.5.7. Виявлення автокореляції. Статистика Дурбіна-Ватсона Найчастіше для виявлення автокорельованості збурень користуються критерієм Дурбіна–Ватсона. При застосуванні цого критерія нульовою гіпотезою є некорельованість збурень, а альтернативою є те, що збурення підпорядковані процесу авторегресії першого порядку. Позначимо через
Можливі значення d належать інтервалу (0; 4). Розподіл статистики Дурбіна–Ватсона приблизно симетричний відносно двійки. Значення d, близькі до 2, вказують на відсутність автокореляції. Значення, близькі до 0, вказують на наявність автокореляції з додатнім r, значення, близькі до 4, вказують на наявність автокореляції з від’ємним r. Параметрами розподілу статистики Дурбіна–Ватсона є кількість спостережень та регресорів. Точний розподіл статистики залежить від матриці незалежних змінних Х. В таблицях приводяться такі пари критичних значень, що для будь-якого вигляду матриці Х точне критичне значення лежить між табличними. Алгоритм застосування критерія Дурбіна–Ватсона полягає у наступному. 1. Оцінюємо модель (1.94) за допомогою звичайного методу найменших квадратів. 2. За формулою (1.118) обчислюємо значення статистики Дурбіна–Ватсона. 3. Вибираємо рівень значущості a і за таблицею критичних значень статистики Дурбіна–Ватсона знаходимо верхнє і нижнє критичні значення du та dl, а також обчислюємо 4 – du та 4 – dl. Зауважимо, що 0 < dl < du < 2 < 4 – du < 4 – dl < 4. 4. Робимо висновок за таким правилом: 1) Якщо d < dl, то має місце автокореляція з додатнім r. 2) Якщо dl < d < du, то ми не можемо зробити ніякого висновку, і цей інтервал називається областю невизначеності. 3) Якщо du < d < 4 – du, то автокореляція відсутня. 4) Якщо 4 – du < d < 4– dl, то ми не можемо зробити ніякого висновку. Цей інтервал також є областю невизначеності. 5) Якщо 4 – dl < d < 4, то має місце автокореляція з від’ємним r. Щодо областей невизначеності можна дати таку практичну рекомендацію: якщо вибіркове значення d потрапляє до інтервалу невизначеності, то вважають, що має місце автокореляція.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 529; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.117.122 (0.012 с.) |

 (1.92)
(1.92)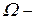 діагональна матриця,
діагональна матриця,  діагональний елемент якої дорівнює
діагональний елемент якої дорівнює  , де
, де 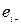 залишки найменших квадратів.
залишки найменших квадратів. .
. , (1.94)
, (1.94)
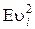 = s2 = const,
= s2 = const,  .
. .
. 1)
1) ,
, ,
, .
.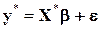 . (1.96)
. (1.96)

 . (1.97)
. (1.97) , а також тим, що лінійний множник можна виносити за знак математичного сподівання. З (1.97) випливає, що модель (1.96) є моделлю класичної лiнiйної регресiї. Отже, оцiнки вектора параметрів регресії b,знайдені в моделi (1.96) методом найменших квадратів мають бажанi статистичнi властивостi, тобто задовольняють теоремі Гауса–Маркова і, що є для нас головним, цими оцінками можна користуватись для статистичних висновків.
, а також тим, що лінійний множник можна виносити за знак математичного сподівання. З (1.97) випливає, що модель (1.96) є моделлю класичної лiнiйної регресiї. Отже, оцiнки вектора параметрів регресії b,знайдені в моделi (1.96) методом найменших квадратів мають бажанi статистичнi властивостi, тобто задовольняють теоремі Гауса–Маркова і, що є для нас головним, цими оцінками можна користуватись для статистичних висновків. невiдомих параметрiв. Отже, потрібно робити певнi припущення щодо збурень – розглядати моделi зi збуреннями спецiального вигляду. Найчастіше розглядаються моделі, зі збуреннями, пiдпорядкованими процесу авторегресiї першого порядку.
невiдомих параметрiв. Отже, потрібно робити певнi припущення щодо збурень – розглядати моделi зi збуреннями спецiального вигляду. Найчастіше розглядаються моделі, зі збуреннями, пiдпорядкованими процесу авторегресiї першого порядку. 1,
1,  . (1.101)
. (1.101) (1.102)
(1.102)
 , (1.106)
, (1.106) (1.107)
(1.107) . Для знаходження коваріації першого порядку домножимо рівність (1.98) почленно на u i -1 і обчислимо математичне сподівання обох частин:
. Для знаходження коваріації першого порядку домножимо рівність (1.98) почленно на u i -1 і обчислимо математичне сподівання обох частин:
 , (1.108)
, (1.108)
 (1.109)
(1.109)
 (1.110)
(1.110)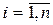 задовольняють співвідношенням (1.98)-(1.105). З (1.107) і (1.110) випливає, що коваріаційна матриця збурень приймає наступний вигляд
задовольняють співвідношенням (1.98)-(1.105). З (1.107) і (1.110) випливає, що коваріаційна матриця збурень приймає наступний вигляд (1.111)
(1.111) у цьому випадку можна записати у явному вигляді. Елементи вектора y* дорівнюють
у цьому випадку можна записати у явному вигляді. Елементи вектора y* дорівнюють , (1.112)
, (1.112) . (1.113)
. (1.113) ) стовпчика матриці X* знаходяться аналогічно:
) стовпчика матриці X* знаходяться аналогічно: , (1.114)
, (1.114) . (1.115)
. (1.115) , значення якої дорівнюють
, значення якої дорівнюють , (1.116)
, (1.116) . (1.117)
. (1.117)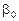 -коефіціента при змінній
-коефіціента при змінній 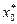 є оцінкою постійного доданку у вихідній моделі.
є оцінкою постійного доданку у вихідній моделі. залишки методу найменших квадратів у моделі (1.94). Значення статистики Дурбіна–Ватсона знаходиться за наступною формулою:
залишки методу найменших квадратів у моделі (1.94). Значення статистики Дурбіна–Ватсона знаходиться за наступною формулою: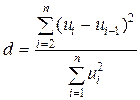 . (1.118)
. (1.118)


