
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оператор лагу і моделі з раціонально розподіленими лагамиСодержание книги
Поиск на нашем сайте
Оператор лагу
Наведемо деякі корисні алгебраїчні властивості оператора лагу
де З використанням оператора лагу основна модель (2.35) набуде вигдяду
де поліном відносно Вираз
Підставимо (2.50)до (2.48), поклавши
Помножимо обидві частини останньої рівності на
звідки
де і Рівняння (2.51) задає модель з раціонально розподіленними лагами в авторегресійній формі. Ця модель узагальнює дві розглянуті раніше моделі. Поклавши в (2.51)
Моделі з нескінченою довжиною лагів і економічна теорія Всі моделі з нескінченою довжиною лагів розглягуті вище, вдалось привести до авторегресіної форми. Відповідні перетворення мали технічний характер, оскільки здійснювались з метою позбутися від нескінченної кількості невідомих параменрів в моделях. В цьому розділі ми розглянемо приклади з економічної теорії, які безпосередньо призводять до авторегресійної форми моделей з розподіленними лагами.
2.6.1.Модель часткового пристосування Цю модель запропонував Марк Нерль. Він припустив, що поточний рівень пояснюючої змінної
Наприклад, бажаний рівень запасів фірми є функцією від рівня продаж, бажаний рівень капіталу в економіці є функцією випуску. Однак, бажаний рівень не можна спостерігати і, отже, використовувати для оцінювання. Завдяки різним причинам існує різниця між бажаним і фактичним рівнями залежної зміної:
Тобто, з точністю до збурення фактичний приріст залежної зміної Рівняння (2.55) відоме як рівняння часткового пристосування, а Чим Запишемо (2.54) у такому вигляді
З (2.55) видно, що фактичне значення залежної змінної в момент Підставимо (2.53) до (2.55):
Звідси
Якщо не брати до уваги властивості збурень, то (2.56)є авторегресійною формою моделі з геометричним розподілом лагів.
Модель адаптивних очікувань В моделі адаптивних очікувань, запропонованій Кейганом, «очікуваний» рівень пояснюючої змінної
Наприклад, сукупний попит на гроші є функцією очікуваної довгостркової відсоткової ставки, обсяг попиту є функцією очікуваної ціни, рівень споживання є функцією очікуваного або перманентного доходу. Кейган припустив, що очікувані значення коректуються з урахуванням нової інформації:
Оскільки Рівняння (2.58) відоме як «рівняння адаптивних очікувань» або «рівняння навчання на похибках». Коефіцієнт У крайньому випадку Запишемо (2.58)у такому вигляді
звідки видно, що очікуване значення є зваженим середнім фактичного і попереднього очікуваного значення. Підставимо (2.59) до (2.57):
Запишемо (2.60)для моменту
Таким чином, ми одержали модель з геометрично розподіленими лагами, записану а авторегресійній формі. Якщо збурення у вихідній моделі (2.62) є класичними (тобто гомоскедастичними і некорельованими), то збурення в моделі, записаній у вигляді (2.61) генеруються процесом MA(1). Однак не слід думати, що модель адаптивних очікувань з необхідністю веде до появи автокорельованих збурень в авторегресійній формі моделі. Наприклад, якщо в (2.57) et= (1-d) et-1+ut, то ut являють собою збурення в моделі (2.61). Зрозуміло, що ut можуть бути некорельованими і гомоскедастичними. Оскільки апріорі невідомо, якими є властивості збурень вихідної моделі в конкретних ситуаціях, то зі сказаного можна зробити висновок, що та чи інша економічна модель, яка призводить до моделі з геометричними лагами, взята сама по собі, не визначає властивості збурень в авторегресійному вигляді останньої. Отже, на нашу думку, правильним підходом буде статистичне визначення властивостей збурень в кожній конкретній ситуації.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.157.203 (0.006 с.) |

 вводиться для спрощення викладок. Він визначається за допомогою співвідношення
вводиться для спрощення викладок. Він визначається за допомогою співвідношення
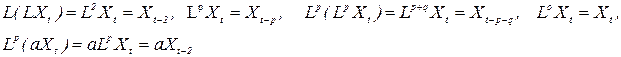
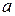 - костанта.
- костанта.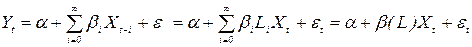 (2.48)
(2.48)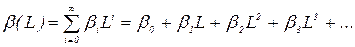 (2.49)
(2.49) як збіжний степеневий ряд можна проінтерпретувати як розклад в ряд Тейлора функції
як збіжний степеневий ряд можна проінтерпретувати як розклад в ряд Тейлора функції 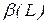 . Йоргенсон в запропонував розглянути моделі, в яких функція
. Йоргенсон в запропонував розглянути моделі, в яких функція 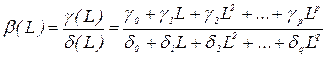 (2.50)
(2.50) :
: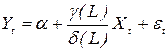
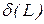 :
: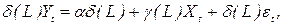
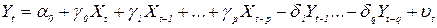 (2.51)
(2.51)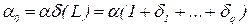
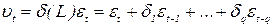 (2.52)
(2.52)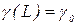 і
і 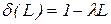 одержуємо модель з геометрично розподіленими лагами. Модель з розподілом лагів Паскаля одержуємо, якщо
одержуємо модель з геометрично розподіленими лагами. Модель з розподілом лагів Паскаля одержуємо, якщо 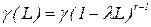 і
і  .
.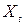 визначає «бажаний» рівень залежної зміної
визначає «бажаний» рівень залежної зміної 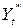 :
: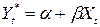 (2.53).
(2.53). (2.54)
(2.54) є меньшим від бажаного в
є меньшим від бажаного в 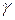 разів.
разів.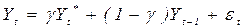 (2.55)
(2.55)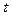 дорівнює зваженому середньому її бажаного значення в момент
дорівнює зваженому середньому її бажаного значення в момент  і фактичному значенню в момент
і фактичному значенню в момент 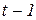 .
.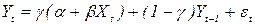
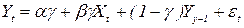 (2.56)
(2.56)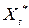 визначає поточний рівень залежної змінної
визначає поточний рівень залежної змінної 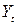 :
: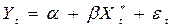 (2.57)
(2.57) (2.58)
(2.58) , то зміна очікуваного рівня
, то зміна очікуваного рівня  є завжди меньшою ніж різниця між фпктичним значенням
є завжди меньшою ніж різниця між фпктичним значенням  і його очікуваним значеням
і його очікуваним значеням 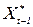 .
.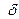 називається «коефіцієнтом очікувань». Чим більше
називається «коефіцієнтом очікувань». Чим більше 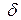 , тим в більшій мірі реалізуються очікування в період
, тим в більшій мірі реалізуються очікування в період 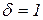 всі очікування реалізуються протягом поточного періоду.
всі очікування реалізуються протягом поточного періоду.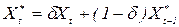 (2.59)
(2.59) (2.60)
(2.60)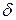 ) і віднімемо від (2.59):
) і віднімемо від (2.59): (2.61)
(2.61)


