
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
У матричному вигляді гіпотеза про сукупність лінійних обмежень записується так,Содержание книги
Поиск на нашем сайте R b = q, де R i q відомі. Кількість рядків матриці R дорівнює кількості обмежень, а кількість стовпчиків – кількості компонент b. Оскільки рівняння вібіркової регресії є рівнянням лінійної функції, то модель лінійної регресії має наступну властивість. При зміні xj на одиницю y зміниться на bj, якими б не були значення решти змінних. Оскільки різні фактори часто взаємодіють між собою, дана властивість не завжди є реалістичною. Тому, щоб відобразити цю взаємодію, доцільно також спробувати включити до моделі добутки вихідних незалежних змінних як нові незалежні змінні. Наприклад, разом з моделлю.
можна розглянути модель
Якщо в моделі (1.65) x 1 зміниться на одиницю, а x 2 та x 3 залишаться постійними, то y зміниться на b1 + g1 x 2 + g2 x 3. Отже, величина зміни незалежної змінної залежить від значень x 2 та x 3. Цей ефект виникає внаслідок того, що різні незалежні змінні взаємодіють між собою. Щоб перевірити, чи є взаємодія несуттєвою, потрібно перевірити гіпотезу H0: Ми побачили, як виникають задачі перевірки гіпотез про лінійні обмеження. Тепер перейдемо до їх розв’язку. Припустимо, ми маємо рівняння множинної регресії:
Нам потрібно перевірити гіпотезу про обмеження: H0: У матричному вигляді гіпотеза формулюється так: R b = q, де
Гіпотеза перевіряється за допомогою критерія Вальда (див. параграф 1.6.5). Статистика, розподіл якої за умови вірності обмежень є розподілом Фішера (кількості степенів свободи = кількість обмежень,r, і n-k), має вигляд
В залежності від наявного програмного засобу зручніше використовувати перший чи другий варіант формули. Опишемо, як скористатись другим способом. Для цього треба знайти суму квадратів залишків RSSU у вихідній моделі та суму квадратів залишків RSSR y моделі з обмеженнями. Запишемо обмеження у такому вигляді:
Підставимо ці співвідношення до рівняння (1.66)
Перенесемо в (1.69) всі відомі величини до правої частини рівняння і зберемо подібні при параметрах регресії в його лівій частині:
Щоб знайти суму квадратів залишків RSSR y моделі з обмеженнями, потрібно оцінити регресію змінної
1.2.11 Перевірка гіпотез про стійкість моделі Припустимо, що ми хочемо побудувати модель деякої економічної системи за даними, що є часовими рядами. Нехай, наприклад, потрібно оцінити макроекономічну виробничу функцію для деякої країни за щорічними даними, причому на протязі періоду, який досліджується, відбулась економічна реформа. Природньо постає питання: чи маємо ми право користуватись єдиною моделлю на протязі всього періоду часу. Відповідь на подібні питання можна одержати за допомогою дослідження моделі на стійкість. Критерій дисперсійного аналізу (критерій переломної точки Чау) Розглянемо модель
У нашому розпорядженні є n спостережень, які розбито на дві групи з n 1та n 2спостережень відповідно (n = n 1 + n 2). Гіпотеза про стійкість моделі полягає у тому, що параметри регресії однакові для обох груп спостережень. Для перевірки гіпотези потрібно оцінити модель (2.42) тричі: за всіма спостереженнями і кожною групою окремо. Введемо такі позначення: RSS – сума квадратів залишків у моделі, яка оцінена за всіма n спостереженнями, RSS1 – сума квадратів залишків у моделі, яка оцінена за першими n1 спостереженнями RSS2 – сума квадратів залишків у моделі, яка оцінена за останніми n2 спостереженнями. Якщо гіпотеза про стійкість моделі вірна, то
Прогностичний Критерій Чау Застосовується у випадках, коли одна з двох груп нараховує невелику кількість спостережень, недостатню для знаходження оцінок. Нехай, для визначеності, n 1 > n 2. Для перевірки гіпотези потрібно оцінити модель (1.70) двічі: за всіма спостереженнями і за більшою групою. Позначимо: RSS – сума квадратів залишків у моделі, яка оцінена за всіма n спостереженнями, RSS1 – сума квадратів залишків у моделі, яка оцінена за більшою групою з n 1 спостереження. Якщо гіпотеза про стійкість моделі вірна, то
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 448; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.009 с.) |


 . (1.65)
. (1.65)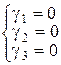 .
. . (1.67)
. (1.67) ,
, 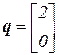 ,
,  .
.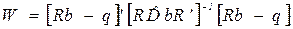 =
=  , (1.68)
, (1.68)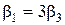 та
та  .
. . (1.69)
. (1.69)
 відносно
відносно 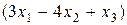 і константи.
і константи. (1.70)
(1.70) . (1.71)
. (1.71) . (1.72)
. (1.72)


