
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Економічні і економетричні моделіСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте ВСТУП Що таке економетрика Економетрика[1] – це галузь економічної теорії, яка вивчає моделі економічних систем у формі, що уможливлює перевірку цих моделей на адекватність засобами математичної статистики. Мета економетрики – здійснювати емпіричну перевірку положень економічної теорії, підтверджуючи чи відхиляючи останні. Цим економетрика відрізняється від математичної економіки, зміст якої полягає виключно у застосуванні математики, і теоретичні положення якої не обов’язково потребують емпіричного підтвердження. Економетрика є результатом синтезу економічної теорії, математичної статистики та економічної статистики. Застосування статистичних методів до аналізу економічних даних має давню історію. Стіглер[2] зауважує, що перша «емпірична» крива попиту була опублікована Чарльзом Дейвенентом у 1699 році, а перше сучасне статистичне дослідження попиту було виконано італійським статистиком Родульфо Еніні у 1907 році. Важливим поштовхом до розвитку економетрики було заснування у 1930 році у США Економетричного Товариства і публікація часопису Econometrica (який, до речі, виходить і досі). Економічні і економетричні моделі Економічна модель являє собою набір припущень, які приблизно описують поведінку економіки (або сектора економіки). Економетрична модель складається з таких частин: 1). Набір рівнянь поведінки, які виводяться з економічної моделі. Ці рівняння включають деякі змінні, значення яких спостерігаються, а також «збурення», які відтворюють ефект від змінних, не включених до моделі у явному вигляді, та ефект від непередбачуваних подій. 2). Опис імовірнісного розподілу «збурень». Економетричні моделі мають стохастичний характер. Розглянемо співвідношення між споживанням С та доходом Y у такому вигляді: С = a + b Y + e, (В.1) де e – збурення, або стохастична складова моделі, a і b – невідомі параметри, які можна оцінити за допомогою методів математичної статистики. Стохастичний характер економетричних моделей дозволяє використовувати теорію статистичних висновків для перевірки цих моделей на адекватність. Перевірка складається з двох етапів: статистичного і економічного. На статистичному етапі ми перевіряємо, чи виконуються вимоги, які накладено на стохастичну складову e при формулюванні моделі. На економічному етапі ми перевіряємо, чи узгоджуються знайдені оцінки параметрів з положеннями економічної теорії. Наприклад, теорія споживання стерджує, що зі зростанням доходу споживання зростає, але не в такій мірі як доход. Звідси випливає, що модель (В.1) коректна, коли в ній 0 < b < 1. Таким чином, економетричні методи дозволяють не тільки встановлювати кількісні зв’язки між економічними змінними, але й робити висновки про коректність одержаних моделей. В першому розділі книзі подано огляд результатів стосовно базової економетричної моделі – моделі лінійної регресії, в тому числі теми, які традиційно не включаються до елементарних курсів економетрики: асимптотична теорія, автокореляція внаслідок неправильної специфікації моделі, спатіальна автокореляція, консистентні в умовах гетероскедастичності оцінки коваріаційної матриці для МНК, метод максимальної правдоподібності включаючи оцінювання коваріаційної матриці і три основні принципи перевірки гіпотез. Розділ 2 присвячений моделям з лаговим змінним. В Розділі розглядаються (більш грунтовно, ніж в елементарних курсах) системи одночасних рівнянь, а в Розділі 4 – моделі з обмеженою залежною змінною і моделі з панельними даними. В Додатку 2. Приведено коротке керівництво користувача програми Eviews. ЗМІСТ
РОЗДІЛ 1. ЛІНІЙНА РЕГРЕСІЯ Проста лінійна регресія Опис Моделі Припустимо, що існують дві змінні x i y, де x - незалежна змінна (регресор), y - залежна змінна. Співвідношення між цими змінними позначимо: y = f (x). Будемо розрізняти детерміновані і статистичні співвідношення. При статистичному співвідношенні кожному значенню x відповідає не єдине значення y, але залежну змінну y можливо точно описати у імовірнісних термінах. Припустимо, що функція f(x) лінійна за x, тобто f(x) = a + b x, а співвідношення між x та y є статистичним, а саме y = a + b x + e, (1.1) де доданок e називається збуренням або похибкою і має відомий імовірносний розподіл (тобто є випадковою величиною). В рівнянні (1.1) a + b x є детермінованим компонентом, збурення e є випадковим або стохастичним компонентом; a і b називаються регресійними коефіцієнтами або параметрами регресії, які потрібно оцінити на основі даних про x та y. Нехай ми маємо n пар значень yi = a + b xi + e i (1.2)
Наша мета - знайти оцінки невідомих параметрів a та b в рівнянні (1.2) на основі n спостережень x та y. Щоб це зробити ми повинні накласти деякі умови щодо збурень e i. 1. Нульове середнє: Ee i = 0, 2. Рівність дисперсій (гомоскедастичність): De i = E 3. Незалежність збурень: e і та e j незалежні при 4. Незалежність збурень та регресора: xi та e j незалежні для всіх i та j. Якщо xi вважаються невипадковими, то дане припущення виконано автоматично. В деяких випадках будемо накладати додаткове припущення (ми будемо вказувати в тексті, для виконнання яких результатів воно необхідно): 5. Нормальність. Збурення e i нормально розподілені для всіх i. Взявши до уваги припущення 1-3, ми можемо сказати, що e i – незалежні нормально розподілені випадкові величини з нульовим математичним сподіванням і однаковими дисперсіями s2, або Отже, модель простої лінійної регресії описується за допомогою рівнянь (1.2), збурення в яких задовольняють припущенням 1 – 5. Оскільки Ee i = 0, то з рівняння (1.2) маємо E(yi) = Друге припущення означає,що для кожного спостереження дія випадкових факторів в середньому однакова. Третє припущення означає, що для кожного спостереження випадкові фактори діють незалежно.
1.1.1. Знаходження оцінок параметрів регресії методом найменших квадратів Нехай
Позначимо на координатній площині точки Щоб мінімізувати вираз (1.3), запишемо необхідну умову екстремуму, тобто прирівняємо похідні відносно
звідки
і
звідки
Система рівнянь (1.4) і (1.5) називається системою нормальних рівнянь. Уведемо такі позначення:
Нехай Sxx> 0. Запишемо розв’язок системи нормальних рівнянь відносно
Розділимо чисельник і знаменник виразу (1.6) на n. Враховуючи уведені позначення, остаточно одержимо:
Якщо обчислити матрицю других похідних для Q, то можна побачити, що ця матриця додатньо визначена, отже значення (1.7) дійсно мінімізують (1.3). Рівняння вибіркої регресії приймає вигляд
З першого нормального рівняння випливає, що графік вибіркової регресійної прямої (1.8) проходить через точку середеніх значень залежної та незалежної змінних. Рівняння (1.8) дає нам уявлення про характер залежності (точніше детермінованої її частини) між змінними x та y. 1.1.3.Властивості залишків методу найменших квадратів Позначимо через
– залишки методу найменших квадратів (аналогічно тому, як ми домовились щодо позначень оцінок методом найменших квадратів, замість загального позначення залишків
Отже, сума залишків методу найменших квадратів дорівнює нулю. Друге нормальне рівняння прийме вигляд
Або, якщо позначити через x вектор значень незажної змінної, а через e вектор залишків:
то
1.1.4.Розклад дисперсії залежної змінної. Коефіціент детермінації З рівнянь (1.8) та (1.9) випливає, що
Запишемо другу з формул (1.7) у вигляді
Від кожного з рівняннь (1.12) віднімемо рівняння (1.13):
Кожне з рівнянь (1.14) піднесемо до квадрату і додамо почленно. Маємо
внаслідок (1.10) та (1.11). Позначимо
Порівнюючи останнє рівняння з (1.14), бачимо, що
отже
Уведемо такі позначення:
Загальна сума квадратів пропорційна до вибіркової дисперсії залежної змінної. Пояснена сума квадратів пропорційна до вибіркової дисперсії незалежної змінної. Отже, дисперсія залежної змінної складається з двох частин. Перша виникає завдяки розкиду значень незалежної змінної. Тобто, ця частина пояснюється за рахунок моделі (звідси і назва – пояснена сума квадратів). Друга частина – сума квадратів залишків – виникає внаслідок збурень і не пояснюється за рахунок моделі. Записавши співвідношення (1.15) з урахуванням уведених позначень, одержимо формулу розкладу дисперсії:
Коефіціент детермінаціїї
Для обчислення коефіціента детермінації можна користуватись такими формулами
Коефіціент детермінації є частиною дисперсії залежної змінної, яка пояснюється за рахунок моделі, або, іншими словами, завдяки мінливості незалежної змінної. Коефіціент детермінації є мірою тісноти саме лінійного зв¢язку між x та y. Коефіціент детермінації завжди знаходиться в межах від нуля до одиниці. Чим ближче
Рис 1.2. У випадку, зображеному на Рис. 1.2.а) має місце досить тісний лінійний зв’язок між змінними. У випадках б) та в) лінійний зв’язок практично відсутній. Однак між цими двома ситуаціями існує істотна різниця. На Рис. 1.2 б), очевидно, відсутній будь-який зв’язок між змінними, тоді як точки на Рис. 1.2.в) розташовані навколо деякої параболи. 1.1.5.Статистичні властивості оцінок методу найменших квадратів Оцінки методу найменших квадратів є незміщеними1): E b = b, E a = a. Дисперсії та коваріація оцінок методу найменших квадратів обчислюються за наступними формулами:
Наведені формули не можна використовувати для перевірки гіпотез та інтервального оцінювання, оскільки до них входить невідомий параметр – дисперсія збурень s2. Отже, нам потрібно вміти знаходити її оцінку. Має місце наступний результат: статистика
є незміщеною оцінкою s2. Якщо збурення нормально розподілені, то a та b також нормально розподілені. Величина
має c2 - розподіл з n - 2 ступенями свободи. Більше того, випадкова величина RSS не залежить від a та b. Далі ми будемо припускати, що збурення нормально розподілені. Як відомо, якщо випадкові величини x1~N(0,1), x2~
має розподіл Стьюдента з p ступенями свободи. Оскільки
має розподіл Стьюдента з n - 2 ступенями свободи. Величина
1.1.6.Статистичні висновки в моделі простої лінійної регресії Інтервальне оцінювання Інтервальна оцінка параметра b з рівнем довіри 1-a (не плутати з постійним доданком у регресії) знаходиться за наступною формулою:
де значення t кр знаходиться за вибраним a в таблиці розподілу Стьюдента з n- 2 ступенями свободи. Приклад В Таблиці 1.1. наведено обсяги сукупного доходу у розпорядженні та сукупного споживання для США у постійних доларах 1972 р. Дані з Таблиці 1.1. зображено графічно на на Рис.1.3. З графіка видно, що точки, які відповідають спостереженням, розташовані навколо деякої прямої, отже доцільно розглянути лінійну функцію споживання. Оцінимо її за допомогою моделі простої лінійної регресії: yi = a + b xi + e i, де через xi та yi позначено відповідно рівень доходу і споживання в році 1969 + i (наприклад i = 5 відповідає 1974 року). Спочатку обчислимо Таблиця 1.1.
Рис. 1.3.
= 879,24;
= 793,43;
Sxx = ((751,6 – 879,24)2 + (779,2 – 879,24)2 + (810,3 – 879,24)2 + + (864,7 – 879,24)2 + (857,5 – 879,24)2 + (874,9 – 879,24)2 + + (906,8 – 879,24)2 + (942,9 – 879,24)2 + (988,8 – 879,24)2 + + (1015,7879,24)2) = 67192,4;
Syy = ((672,1 – 793,43)2 + (696,8 – 793,43)2 + (737,1 – 793,43)2 + + (767,9 – 793,43)2 + (762,8 – 793,43)2 + (779,4 – 793,43)2 + + (823,1 – 793,43)2 + (864,3 – 793,43)2 + (903,2 – 793,43)2 + + (927,6 – 793,43)2) = 64972,1;
Sxy = ((751,6 – 879,24) (672,1 – 793,43) + (779,2 – 879,24) (696,8 – 793,43) + + (810,3 – 879,24) (737,1 – 793,43) + (864,7 – 879,24) (767,9 – 793,43) + + (857,5 – 879,24) (762,8 – 793,43) + (874,9 – 879,24) (779,4 – 793,43) + + (906,8 – 879,24) (823,1 – 793,43) + (942,9 – 879,24) (864,3 – 793,43) + +(988,8 – 879,24) (903,2 – 793,43) + (1015,7879,24) (927,6 – 793,43)) = = 65799,3. За формулами (1.7) знаходими оцінки методу найменших квадратів коефіцієнгів моделі (1.27):
Отже, рівняння вибіркової регресійної прямої (рівняння фунцції споживання) має вигляд:
= 0.979´65799,3/64972,1 = 0.990702. Як ми бачимо, зв’язок між споживанням і доходом є вельми тісним. Перед тим, як використовувати рівняння (1.28) для економічного аналізу або побудови прогнозів, модель (1.27) потрібно перевірити на адекватність. Перевіримо гіпотезу про значущість регресії двома способами. Спочатку використаємо F -статистику (1.23):
Нехай, рівень значущості a дорівнює 0,05. В Таблиці 3. Додатку знаходимо, що критичне значення F кр = 5,32. Ми бачимо, що | F |³ F кр, отже гіпотеза про рівність b нулю відхиляється, тим самим модель (1.27) є значущою. Обчислимо стандартні похибки оцінок. Спочатку знайдемо суму квадратів залишків RSS. За формулою (1.15) RSS = Syy – b 2 Sxx = 64972,1 – 0.9792´67192,4 = 537,0. Далі знаходимо оцінку дисперсії збурень
стандартна похибка b дорювнює:
SE( b) =
Перевіримо гіпотезу про те, що коефіцієнт нахилу регресійної прямої b дорівнює нулю за допомогою t -статистики (1.20):
Нехай, рівень значущості a дорівнює 0,05. В Таблиці 1. Додатку знаходимо, що критичне значення t кр = 2,306. Ми бачимо, що | t |³ t кр, отже гіпотеза відхиляється. Отже, ми можемо вважати модель адекватною (читач не повинен забувати, що повна перевірка моделі на адекватність включає аналіз залишків, з елементами якого ми ознайомимось в розділах 3 та 4). З теорії споживання відомо, що коефіцієнт нахилу лінійної функції споживання є маргінальною або граничною схильністю до споживоння. Таким чином, ми встановили, що в середньому 0.979 ´ 100 = 97,9% прирісту доходу витрачається на споживання1). Обчислене значення граничної схильності до споживання знаходиться в інтервалі (0; 1), що узгоджується з економічною теорією. Множинна лінійна регресія 1.2.1. Опис моделі За допомогою моделі простої лінійної регресіїї ми вивчали зв’язок між залежною змінною y та незалежною змінною x. Модель множинної лінійної регресії описує співвідношення між y та набором незалежних змінних x0, x 1,..., xk -1. Так, наприклад, при дослідженні попиту нас цікавить залежність обсягу попиту на деякий товар від ціни на цей товар, цін на взаємозамінні з даним товари та від доходів споживачів. При наявності n спостережень модель множинної лінійної регресії записується у вигляді
де xij – значення j -ї незалежної змінної (xj) в i -му спостереженні, збурення e i задовольняють тим самим припущенням, що і в моделі простої регресії. 1. Нульове середнє: E e i = 0, 2. Рівність дисперсій: De i = E 3. Незалежність збурень: e і та e j незалежні при 4. Незалежність збурень та регресорів: xij та e і незалежні для всіх i та j (якщо регресори не стохастичні, то дане припущення виконується автоматично). 5. (Додаткове). Збурення e i нормально розподілені для всіх i. Модель множинної лінійної регресії (1.29) зручно записувати у матрично-векторному вигляді:
з використанням наступних позначень:
Матриця X складається з n рядків – відповідно до кількості спостережень, – і з k стовпчиків, кількість яких дорівнює кількості незалежних змінних. Щоб записати модель з константою:
у матричному вигляді, розглядають матрицю значень незалежних змінних, в якій перший стовпчик складається з одиниць:
Позначимо через D e коваріаційну матрицю вектора збурень
внаслідок того, що збурення мають нульові математичні сподівання. Тоді припущення 2 та 3 зручно записувати у вигляді: De =s2 I n, (1.31) де I n – одинична матриця n -го порядку, а припущення 1 – E e = 0. Модель множинної лінійної регресії у матрично-векторних позначеннях:
e не залежить від X Додаткове припущення: e ~ N (0,s2 I)
1.2.2. Знаходження параметрів регресії методом найменших квадратів Нехай
Тоді
є оцінкою E yi, побудованою на основі вибіркової регресіїї. Залишки
Вектор залишків Оцінки методу найменших квадратів знаходяться з умови мінімізації суми квадратів залишків за всіма можливими значеннями
Щоб мінімізувати вираз (1.32), запишемо необхідну умову екстремуму, тобто прирівняємо похідні відносно
тобто, система нормальних рівнянь має вигляд
звідки
Перевірка достатніх умов екстремуму показує, що
Оцінка методу найменших квадратів коефіцієнтів моделі моделі множинної лінійної регресії знаходиться за формулою:
Рівняння вибіркої регресії приймає вигляд
або, у випадку регресії з костантою,
Рівняння вибіркої регресії є рівнянням лінійної функції багатьох змінних. Зауваження 1 Без використання додаткової інформаціїї не можна робити висновків про те, яке значення Зауваження 2 В моделях без константи коефіцієнт детермінації не обов’язково знаходиться в межах від нуля до одиниці, оскількі подвоєний добуток у (1.40) не дорівнює нулю. В таких моделях різні способи визначення
1.2.5. Статистичні властивості оцінок методу найменших квадратів Обчислимо математичне сподівання оцінок методу найменших квадратів. Підставимо формулу (1.30) до формули (1.34):
Маємо
оскільки лінійний множник можна виносити за знак математичного сподівання, і E e = 0. Отже, МНК-оцінки є незміщеними. Знайдемо коваріаційну матрицю оцінки b: Db = E(b - E b)(b - E b)T = E(b - b)(b - b)T =
Ми скористались властивостями математичного сподівання, добутку транспонованих матриць, формулою (1.31), а також тим, що матриця X T X, аотже і обернена до неї, симетричні.
Позначимо матрицю
Наведені формули не можна використовувати для перевірки гіпотез та інтервального оцінювання, оскільки до них входить невідомий параметр – дисперсія збурень s2. Отже, нам потрібно вміти знаходити її оцінку. Має місце наступний результат: статистика
де k – кількість регресорів, включаючи константу, є незміщеною оцінкою s2. Якщо збурення нормально розподілені, то b має багатовимірний нормальний розподіл, математичне сподівання і коваріаційна матриця якого обчислюються за формулою (1.44). Зокрема,
Величина
має c2 - розподіл з n - k ступенями свободи і не залежить від b. Оцінка коваріаційної матриці коефіціентів методу найменших квадратів одержується підстановкою до формули (1.44) виразу (1.46) замість дисперсії збурень s2:
зокрема
Позначимо через s.e. ( bi) оцінку середньокватратичного відхилення коефіціента bi. (стандартнy похибку)
Розмірковуючи так, як у випадку простої регресії, приходимо до висновку, що
Оцінки методу найменших квадратів є лінійними у тому розумінні, що b є лінійною функцією y. Наступна теорема встановлює оптимальні властивості оцінки методу найменших квадратів. Теорема Гауса-Маркова 1) Нехай припущення про нормальність збурень не накладається. Тоді МНК-оцінки мають мінімальну коваріаційну матрицю в класі незміщених лінійних оцінок. 2)Припустимо, що збурення нормально розподілені. МНК- оцінки мають мінімальну коваріаційну матрицю в класі усіх незміщених оцінок. Зокрема, оцінки індивідуальних коефіціентів bi мають найменші дисперсії серед оцінок відповідних класів.
Прогностичний Критерій Чау Застосовується у випадках, коли одна з двох груп нараховує невелику кількість спостережень, недостатню для знаходження оцінок. Нехай, для визначеності, n 1 > n 2. Для перевірки гіпотези потрібно оцінити модель (1.70) двічі: за всіма спостереженнями і за більшою групою. Позначимо: RSS – сума квадратів залишків у моделі, яка оцінена за всіма n спостереженнями, RSS1 – сума квадратів залишків у моделі, яка оцінена за більшою групою з n 1 спостереження. Якщо гіпотеза про стійкість моделі вірна,
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 706; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.02 с.) |

 . Кожну пару будемо називати спостереженням. Ми можемо записати рівняння (1.1) у вигляді
. Кожну пару будемо називати спостереженням. Ми можемо записати рівняння (1.1) у вигляді
 .
. = s2 = const,
= s2 = const, 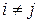 . Зокрема, cov(e i, e j) = Ee i e j = 0 при
. Зокрема, cov(e i, e j) = Ee i e j = 0 при  .
.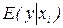 a + b xi. Останній вираз називається популяційною функцією регресії. Таким чином, популяційна функція регресії – функція умовного математичного сподівання. Якщо замінити значення параметрів їх оцінками, одержимо вибіркову функцію регресії. Популяційна регресійна функція дає усереднене, або закономірне значення незалежної змінної, яке відповідає даному значенню незалежної змінної. Збурення можна інтерпретувати як відмінність поведінки залежної змінної від усередненої в кожній конкретній ситуації.
a + b xi. Останній вираз називається популяційною функцією регресії. Таким чином, популяційна функція регресії – функція умовного математичного сподівання. Якщо замінити значення параметрів їх оцінками, одержимо вибіркову функцію регресії. Популяційна регресійна функція дає усереднене, або закономірне значення незалежної змінної, яке відповідає даному значенню незалежної змінної. Збурення можна інтерпретувати як відмінність поведінки залежної змінної від усередненої в кожній конкретній ситуації. та
та  –деякі оцінки параметрів a та b. Запишемо рівняння вибіркової регресії
–деякі оцінки параметрів a та b. Запишемо рівняння вибіркової регресії  . Тоді
. Тоді  є оцінкою E yi, побудованою на основі вибіркової регресії. Позначимо через
є оцінкою E yi, побудованою на основі вибіркової регресії. Позначимо через  різницю між значенням y, яке спостерігалось, і обчисленим з регресії. Оцінки методу найменших квадратів (скорочено – МНК-оцінки) знаходяться з умови мінімізаціїї за всіма можливими значеннями
різницю між значенням y, яке спостерігалось, і обчисленим з регресії. Оцінки методу найменших квадратів (скорочено – МНК-оцінки) знаходяться з умови мінімізаціїї за всіма можливими значеннями  (1.3)
(1.3) і побудуємо графіки прямих
і побудуємо графіки прямих  для різних значень
для різних значень  і
і  . Знаходження оцінок методом найменших квадрвтів означає пошук прямої, яка знаходиться найближче до даних точок у тому розумінні, що сума квадратів відстаней по вертикалі від даних точок до прямої буде найменшою. Обгрунтування такого вибору методу побудови оцінок полягає в їх оптимальних статистичних властивостях, які сформульовано вище.
. Знаходження оцінок методом найменших квадрвтів означає пошук прямої, яка знаходиться найближче до даних точок у тому розумінні, що сума квадратів відстаней по вертикалі від даних точок до прямої буде найменшою. Обгрунтування такого вибору методу побудови оцінок полягає в їх оптимальних статистичних властивостях, які сформульовано вище. ,
,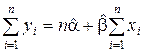 (1.4)
(1.4) ,
, (1.5)
(1.5) ,
, ,
, ,
, ,
,
 (1.6).
(1.6). . Розділимо перше нормальне рівняння (1.4) почленно на n. Маємо:
. Розділимо перше нормальне рівняння (1.4) почленно на n. Маємо:  . Надалі будемо позначати МНК-оцінки параметрів a та b латинськими літерами a та b. Отже, МНК-оцінки параметрів моделі простої лінійної регресії знаходяться за фомулами:
. Надалі будемо позначати МНК-оцінки параметрів a та b латинськими літерами a та b. Отже, МНК-оцінки параметрів моделі простої лінійної регресії знаходяться за фомулами: (1.7)
(1.7) . (1.8)
. (1.8) різниці між фактичними та теретичними, тобто обчисленими з рівняння вибіркої регресії (1.8) значеннями залежної змінної:
різниці між фактичними та теретичними, тобто обчисленими з рівняння вибіркої регресії (1.8) значеннями залежної змінної: (1.9)
(1.9) , для залишків методу найменших квадратів будемо використовувати літеру e). Залишки можна вважати вибірковими, або емпіричними аналогами збурень. З урахуванням уведених позначень перше нормальне рівняння запишеться у вигляді
, для залишків методу найменших квадратів будемо використовувати літеру e). Залишки можна вважати вибірковими, або емпіричними аналогами збурень. З урахуванням уведених позначень перше нормальне рівняння запишеться у вигляді (1.10).
(1.10). (1.11).
(1.11). ,
,  ,
, . Тобто, залишки методу найменших квадратів ортогональні до регресора.
. Тобто, залишки методу найменших квадратів ортогональні до регресора. (1.12)
(1.12) (1.13)
(1.13) (1.14)
(1.14)
 , (1.15)
, (1.15) . З (1.10) випливає, що
. З (1.10) випливає, що  . Тому
. Тому .
. ,
, .
. – загальна сума квадратів,
– загальна сума квадратів,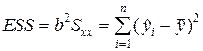 – пояснена сума квадратів, або сума квадратів регресії
– пояснена сума квадратів, або сума квадратів регресії –сума квадратів залишків.
–сума квадратів залишків. (1.16).
(1.16). визначається як частка поясненої і загальної сум квадратів
визначається як частка поясненої і загальної сум квадратів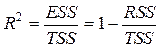 (1.17).
(1.17). . (1.17а)
. (1.17а) до 1, тим точніше x пояснює y. Якщо
до 1, тим точніше x пояснює y. Якщо 


 (1.18)
(1.18)

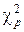 незалежні2), то
незалежні2), то
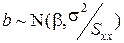 , то
, то  має стандартний нормальний розподіл. Крім того,
має стандартний нормальний розподіл. Крім того,  і ці випадкові величини незалежні. Отже, частка
і ці випадкові величини незалежні. Отже, частка
 є оцінкою дисперсії b, а
є оцінкою дисперсії b, а  – оцінкою середньоквадратичного відхилення, або, коротко, стандартною похибкою оцінки b. Уведемо позначення SE( b) =
– оцінкою середньоквадратичного відхилення, або, коротко, стандартною похибкою оцінки b. Уведемо позначення SE( b) =  (1.19)
(1.19) , (1.22)
, (1.22) , (1.27)
, (1.27)
 =(751,6+779,2+810,3+864,7+857,5+874,9+906,8+942,9+988,8+1015,7)/10 =
=(751,6+779,2+810,3+864,7+857,5+874,9+906,8+942,9+988,8+1015,7)/10 = =(672,1+696,8+737,1+767,9+762,8+779,4+823,1+864,3+903,2+927,6)/10 =
=(672,1+696,8+737,1+767,9+762,8+779,4+823,1+864,3+903,2+927,6)/10 =
 = – 67,58 + 0.979 x. (1.28)
= – 67,58 + 0.979 x. (1.28) Рис 1.4
Рис 1.4
 .
. .
. 0.0316071.
0.0316071. .
. (1.29)
(1.29) = s2 = const,
= s2 = const,  .
. (1.30)
(1.30) –вектор значень залежної змінної,
–вектор значень залежної змінної, – матриця значень незалежних змінних,
– матриця значень незалежних змінних, – вектор збурень,
– вектор збурень, – вектор параметрів (коефіцієнтів) регресії.
– вектор параметрів (коефіцієнтів) регресії.
 .
.
 ,
,
 –деяка оцінка вектора параметрів
–деяка оцінка вектора параметрів  . Запишемо рівняння вибіркої регресії
. Запишемо рівняння вибіркої регресії .
.
 визначаються як різниці між значеннями залежної змінної, які спостерігались, і обчисленими з регресії:
визначаються як різниці між значеннями залежної змінної, які спостерігались, і обчисленими з регресії: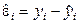 .
. дорівнює
дорівнює  , де
, де  ,
,  .
.
 (1.32)
(1.32) ,
, ,
, . (1.33)
. (1.33) .
. (1.34)
(1.34) . (1.35),
. (1.35), (1.36).
(1.36).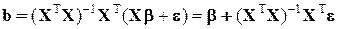 1.43)
1.43) ,
, =
=

 .
.
 (1.44)
(1.44) через
через  . Тоді
. Тоді (1.45)
(1.45) , (1.46)
, (1.46)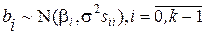 .
.
 , (1.47)
, (1.47) .
.
 (1.48)
(1.48)


