
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості залишків методу найменших квадратівСодержание книги
Поиск на нашем сайте
Нехай
Позначимо
Використовуючи введені векторно-матричні позначення, можна записати
Вектор залишків методу найменших квадратів e визначається як1)
Зміст поняття залишків такий же, як і в моделі простої лінійної регресії. Перепишемо систему нормальних рівнянь у такому вигляді:
або X T e = 0. (1.37) Ми бачимо, що вектор залишків ортогональний до кожного стовпчика матриці X. Згадаємо, що j -й стовпчик цієї матриці утворюють значення j -го регресора. Отже, залишки методу найменших квадратів ортогональні до регресорів. Якщо ми розглядаємо модель з константою, то перший стовпчик матриці X складається з одиниць, і з рівняння (1.37) випливає, що
В моделі з константою сума залишків методу найменших квадратів дорівнює нулю. Оскільки
внаслідок (1.39). Крім того вектор Зі співвідношення (1.39) випливає ще один важливий наслідок: в моделі з костантою регресійна гіперплощина проходить через точку, координати якої дорівнюють середнім значення незалежних змінних. 1.2.4.Розклад дисперсії залежної змінної. Коефіцієнт детермінації В цьому параграфі ми розглянемо моделі з константою. Аналогічно тому, як ми робили у випадку простої регресії, проаналізуємо суму квадратів відхилень значень залежної змінної від середнього – загальну суму квадратів:
внаслідок (1.38), (1.39) і з урахуванням того, що
Коефіцієнт множинної детермінаціїї (або, коротко, коефіцієнт детермінації
Коефіцієнт множинної детермінації показує, яка частина дисперсії залежної змінної пояснюється за рахунок моделі, або, іншими словами, незалежними змінними в сукупності. Підкреслимо, що коефіцієнт детермінації є мірою тісноти саме лінійного зв¢язку між залежною та незалежними змінними. Коефіцієнт детермінації завжди знаходиться в межах від нуля до одиниці. Чим ближче Зауваження 1 Без використання додаткової інформаціїї не можна робити висновків про те, яке значення Зауваження 2 В моделях без константи коефіцієнт детермінації не обов’язково знаходиться в межах від нуля до одиниці, оскількі подвоєний добуток у (1.40) не дорівнює нулю. В таких моделях різні способи визначення
1.2.5. Статистичні властивості оцінок методу найменших квадратів Обчислимо математичне сподівання оцінок методу найменших квадратів. Підставимо формулу (1.30) до формули (1.34):
Маємо
оскільки лінійний множник можна виносити за знак математичного сподівання, і E e = 0. Отже, МНК-оцінки є незміщеними. Знайдемо коваріаційну матрицю оцінки b: Db = E(b - E b)(b - E b)T = E(b - b)(b - b)T =
Ми скористались властивостями математичного сподівання, добутку транспонованих матриць, формулою (1.31), а також тим, що матриця X T X, аотже і обернена до неї, симетричні.
Позначимо матрицю
Наведені формули не можна використовувати для перевірки гіпотез та інтервального оцінювання, оскільки до них входить невідомий параметр – дисперсія збурень s2. Отже, нам потрібно вміти знаходити її оцінку. Має місце наступний результат: статистика
де k – кількість регресорів, включаючи константу, є незміщеною оцінкою s2. Якщо збурення нормально розподілені, то b має багатовимірний нормальний розподіл, математичне сподівання і коваріаційна матриця якого обчислюються за формулою (1.44). Зокрема,
Величина
має c2 - розподіл з n - k ступенями свободи і не залежить від b. Оцінка коваріаційної матриці коефіціентів методу найменших квадратів одержується підстановкою до формули (1.44) виразу (1.46) замість дисперсії збурень s2:
зокрема
Позначимо через s.e. ( bi) оцінку середньокватратичного відхилення коефіціента bi. (стандартнy похибку)
Розмірковуючи так, як у випадку простої регресії, приходимо до висновку, що
Оцінки методу найменших квадратів є лінійними у тому розумінні, що b є лінійною функцією y. Наступна теорема встановлює оптимальні властивості оцінки методу найменших квадратів. Теорема Гауса-Маркова 1) Нехай припущення про нормальність збурень не накладається. Тоді МНК-оцінки мають мінімальну коваріаційну матрицю в класі незміщених лінійних оцінок. 2)Припустимо, що збурення нормально розподілені. МНК- оцінки мають мінімальну коваріаційну матрицю в класі усіх незміщених оцінок. Зокрема, оцінки індивідуальних коефіціентів bi мають найменші дисперсії серед оцінок відповідних класів.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 462; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.105.127 (0.008 с.) |

 .
. .
. .
. .
. ,
, (1.38)
(1.38) , то
, то (1.39)
(1.39) є лінійною комбінацією стовпчиків матриці X, тобто регресорів. Разом з (1.39) це дозволяє дати наступну геометричну інтерпретацію вектору
є лінійною комбінацією стовпчиків матриці X, тобто регресорів. Разом з (1.39) це дозволяє дати наступну геометричну інтерпретацію вектору  і залишкам:
і залишкам:  на гіперплощину, породжену регресорами, а вектор залишків є проектором.
на гіперплощину, породжену регресорами, а вектор залишків є проектором. (1.40)
(1.40) =
=  . Як і раніше,
. Як і раніше,  – пояснена сума квадратів,
– пояснена сума квадратів,  –сума квадратів залишків. Загальна сума квадратів пропорційна до вибіркової дисперсії незалежної змінної. Отже, формула розкладу дисперсії має місце і у випадку множинної регресії
–сума квадратів залишків. Загальна сума квадратів пропорційна до вибіркової дисперсії незалежної змінної. Отже, формула розкладу дисперсії має місце і у випадку множинної регресії (1.41).
(1.41). визначається як частка поясненої і загальної сум квадратів
визначається як частка поясненої і загальної сум квадратів (1.42).
(1.42). до 1, тим тісніше зв¢язок. Якщо
до 1, тим тісніше зв¢язок. Якщо 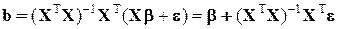 1.43)
1.43) ,
, =
=

 .
.
 (1.44)
(1.44) через
через  . Тоді
. Тоді (1.45)
(1.45) , (1.46)
, (1.46)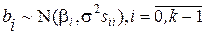 .
.
 , (1.47)
, (1.47) .
.
 (1.48)
(1.48)


