
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оцінювання моделей з нескінченною довжиною лагів.Содержание книги
Поиск на нашем сайте
В цьому параграфі ми коротко і досить неформально розглянемо методи оцінювання моделей з раціональними лагами, приділяючи основну увагу найпростішому випадку – моделям з геометричним розподілом лагів. Відразу наголосимо, що необхідною умовою консистентності оцінок методу найменших квадратів і оцінок інших методів є стаціонарність змінних моделі. Отже, важливо пам’ятати, що моделі з розподіленими лагами є засобом дослідження зв’язків між стаціонарними змінними. В протилежному випадку в деяких випадках вдається відшукати “стабілізуючі” перетворення, такі як перехід до різниць (як це робиться при моделюванні Бокса–Дженкінса), або до відносних приростів. Звернімо увагу на те, що в прикладах, розглянутих на початку розділу, деякі змінні відразу розглядались у вигляді приростів, що диктувалось теорією, покладеною в основу відповідних моделей. Якщо змінні стають стаціонарними в результаті виділення детермінистичного тренду, наприклад, лінійного, то проблема вирішується шляхом включення в модель відповідного тренда. Найбільш уживаним способом дослідження залежностей між нестаціонарними змінними є модель корекції похибок. Як зазначалось вище, моделі з (раціонально)розподіленими лагами можна записувати у двох формах: авторегресійній і рухомого середнього. Тому оцінювати модель можна в будь-якій з цих форм. 7.1. Оцінювання у авторегресійній формі. Авторегресійна форма моделі з раціонально розподіленими лагами у випадку єдиної пояснюючої змінної має вигляд
де et – збурення, а кількості k– 1 i l лагових значень визначаються на відміну від випадку необмежених лагів вихідним виглядом моделі (у формі рухомого середнього). Наприклад, як ми побачили в параграфі 6, авторегресійна форма моделі з геометричним розподілом лагів є такою
а для лагів Паскаля з r =2 маємо:
Методи оцінювання залежать від стохастичної специфікації збурень. При виконанні класичних умов оцінки методу найменших квадратів будуть консистентними, хоча і зміщеними. Складнішою буде ситуація у випаку автокорельованих збурень. В цьому місці буде доречним нагадати про некоректність використання критерія Дурбіна–Ватсона для перевірки автокорельованості збурень у випадку наявності лагових значень залежної змінної (див. параграф. 1.5.9) У численних джерелах можна зустріти твердження про неконсистентність оцінок методу найменших квадратів за умов наявності лагових значень залежної змінної і автокорельованих збурень. Однак, без подальших уточнень, це твердження може виявитись хибним. Так, можна навести приклад структури автокореляції збурень в моделі (2.63), при якій Інструментами для регресора X називаються змінні Z, які корельовані з X, але не корельовані з поточними збуреннями. Для знаходження оцінок потрібно відшукати принаймі не менше інструментів (які відсутні в моделі), ніж кількість ендогенних регресорів, тобто тих, які корельовані з поточними збуреннями. Техніку обчислень простіше за все описати так. Оцінювання здійснюється в два етапи. На першому етапі звичайним методом найменших квадратів оцінюються регресії ендогенних регресорів відносно інструментів, в число яких включають регресори моделі, некореьовані з поточними регресорами (екзогенні регресори). На другому етапі також звичайним методом найменших квадратів оцінюється вихідна модель, в якій значення ендогенних регресорів, замінюються на свої оцінки, знайдені на першому етапі. Двохетапний метод найменших квадратів, який застосовується для оцінювання систем одночасних рівнянь, є варіантом методу інструментальних змінних, зумовленим конкретним вибором інструментів. Тому зараз немає потреби розглядати коваріаційну матрицю для цих оцінок, оскільки її наведено в розділі, присвяченому системам одночсних рівнянь. Вивір належного набору інструментів в деяких випадках становить складну практичну проблему, але у випадку моделей з автогегресійними лагами завжди можна запропонувати один очевидний розв’язок: в моделі (2.62) використати як інструменти лагові значення X з лагом, більшим, ніж k. Наприклад, в моделі (2.63) інструментами можуть слугувати Xt-1, Xt-2, …. Для коваріаційної матриці оцінок методу інструментальних змінних також існують аналоги оцінки Неві–Веста на випадок автокорельованих збурень. При виконанні стандартних умов регулярності оцінки методу інструментальних змінних будуть консистентними і асимптотично нормально розподіленими, хоча і не будуть асимптотично ефективними. Однак, їх коректність не потребує припущень про структуру автокореляції збурень (а, отже не залежить від помилок при її визначенні). Цим пояснюється надійність методу. Крім того, при відомій структурі автокореляції збурень на другому етапі можна застосувати варіант узагальненого методу найменших квадратів, пристосований до наявного типу автокореляції збурень. На практиці нас частіше цікавлять оцінки параметрів вихідної форми моделі. Отже їх необхідно виразити через параметри авторегресійної форми моделі, а потім в одержані формули підставити знайдені оцінки. Дисперсії можна знайти з використанням формули асимптотичної дисперсії нелінійних функцій від параметрів. Знаючи конкретну структуру збурень (наприклад ARMA(p,q)), можна застосувати метод максимальної правдоподібності. Вигляд функції правдоподібності у випадку MA-збурень є складним і на практиці можуть виникати проблеми зі збіжністю. У випадку авторегресійних збурень існує інша дуже проста можливість. Припустимо, що в моделі (2.63) збурення генеруються процесом AR(1). Якщо записати (2.63) для моменту t–1 і з одержаного рівняння виразити 7.2 Оцінювання у формі рухомого середнього. Оцінювання здійснюється методом максимальної правдоподібності або нелінійним методом найменших квадратів, а отже ми завжди маємо спиратись на припущення про конкретну структуру автокореляції збурень. Як завжди, три найбільш розповсюджені ситуації: класичні збурення, AR(1)–збурення і МА(1)-збурення. Ми обмежимось розглядом моделі з геометричним розподілом лагів з класичними і AR(1)–збуреннями. Класичні збурення Нам буде зручно скористатись записом моделі у вигляді (2.44):
Перетворимо (2.65) до такого вигляду:
Нехай
де В умовах нормально розподілених збурень логарифмічна функція правдоподібності для цієї моделі нелінійної регресії має такий вигляд
де Аналізуючи вигляд функції (2.67), легко зрозуміти, що оцінки максимальної правдоподібності співпадають з оцінками нелінійного методу найменших квадратів. Оцінка дисперсії збурень знаходиться за звичною формулою
Без припущення про нормальність збурень оцінки нелінійного методу найменших квадратів лишаються консистентними, хоча і можуть виявитись неефективними. Для фіксованого значення l оцінки решти параметрів, тобто a, q=b(1-l), та m0 можна знайти з лінійної регресії Yt відносно константи,
Оцінки стандартних похибок можна знайти за допомогою оберненої до інформаційної матриці. Остання має такий вигляд
де
Вибіркові значення
(2.70)
і
Нарешті,
Асимтотичну дисперсію останньої оцінки можна оцінити, використовуючи формулу асимтотичної дисперсії нелінійної функції від параметрів:
Автокорельовані (AR(1)) збурення. Якщо збурення в (2.66) генеруються процесом AR(1):
то описаний вище алгоритм можна застосувати до перетвореної моделі:
При заданому значенні r в точності повторюєть дії у випадку некорельованих збурень. Для пошуку всього набору параметрів можна організувати двовимірний решітковий пошук l і r.
Моделі з панельними даними. Переваги панельних даних. Панельні дані або панель утворюється таким чином. Припустимо, що ми маємо
де
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.5.216 (0.012 с.) |

 , (2.62)
, (2.62) , (2.63)
, (2.63) . (2.64)
. (2.64)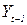 виявляється некорельованим з
виявляється некорельованим з 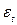 . У такому випадку коректно застосувати звичайний метод найменших квадратів з використанням оцінки Неві–Веста для коваріаційної матриці оцінок параметрів. В інших випадках, наприклад для AR(1) - або для MA(1) – збурень в моделі (2.63),
. У такому випадку коректно застосувати звичайний метод найменших квадратів з використанням оцінки Неві–Веста для коваріаційної матриці оцінок параметрів. В інших випадках, наприклад для AR(1) - або для MA(1) – збурень в моделі (2.63),  і підставити в рівняння (2.63), в якому збурення записано з використанням означення процесу AR(1), то після перепозначення параметрів одержимо рівняння (2.64) з нелінійним обмеженням на параметри. Це обмеження нескладно перевірити. Якщо воно хибне, то це означає що потрібно вибрати модель (2.64). Іншими словами, у вихідній моделі замість геометричного слід використати розподіл лагів Паскаля. Таким чином, у випадку авторегресійних збурень буває можливим звільнитись від автокореляції шляхом включення в авторегресійну форму моделі додаткових лагів, а отже, врешті решт скористатись звичайним методом найменших квадратів в модифікованій моделі.
і підставити в рівняння (2.63), в якому збурення записано з використанням означення процесу AR(1), то після перепозначення параметрів одержимо рівняння (2.64) з нелінійним обмеженням на параметри. Це обмеження нескладно перевірити. Якщо воно хибне, то це означає що потрібно вибрати модель (2.64). Іншими словами, у вихідній моделі замість геометричного слід використати розподіл лагів Паскаля. Таким чином, у випадку авторегресійних збурень буває можливим звільнитись від автокореляції шляхом включення в авторегресійну форму моделі додаткових лагів, а отже, врешті решт скористатись звичайним методом найменших квадратів в модифікованій моделі.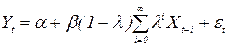 (2.65).
(2.65).
 .
.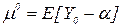 . Неважко бачити, що третій доданок дорівнює
. Неважко бачити, що третій доданок дорівнює  . Логічно інтерпретувати
. Логічно інтерпретувати  як невідомий параметр. Дійсно ми не маємо вибіркової інформації про момент часу 0. Такм чином, модель набуває вигляду
як невідомий параметр. Дійсно ми не маємо вибіркової інформації про момент часу 0. Такм чином, модель набуває вигляду ,
,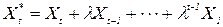 (2.66)
(2.66) (2.67)
(2.67) .
.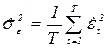 .
. і
і  . Оскільки l лежить між нулем і одиницею, на практиці можна застосувати решітковий пошук. Стандартно спочатку для кожного l =0,1; 0,2; …;0,9 оцінюють лінійні регресії і в результаті вибирають значення
. Оскільки l лежить між нулем і одиницею, на практиці можна застосувати решітковий пошук. Стандартно спочатку для кожного l =0,1; 0,2; …;0,9 оцінюють лінійні регресії і в результаті вибирають значення  , яке дає найменшу суму квадратів залишків. На другому етапі процедура повторюється в діапазоні [
, яке дає найменшу суму квадратів залишків. На другому етапі процедура повторюється в діапазоні [ 

 (2.68)
(2.68)
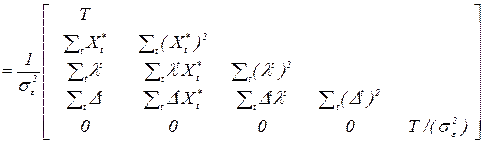 (2.69)
(2.69)
 .
. також можна знайти за допомогою рекурентної формули. Використовуючи (2.68), можна показати, що
також можна знайти за допомогою рекурентної формули. Використовуючи (2.68), можна показати, що ,
,

 (2.71)
(2.71) (2.72)
(2.72)


 одиниць спостереження
одиниць спостереження  , причому для кожної одиниці (особ, домогосподарств, фірм, галузей промисловостей, країн, тощо) ми спостерігаємо набір показників з
, причому для кожної одиниці (особ, домогосподарств, фірм, галузей промисловостей, країн, тощо) ми спостерігаємо набір показників з  періодів часу. Через
періодів часу. Через  Будемо позначати значення залежної змінної для
Будемо позначати значення залежної змінної для  в момент часу
в момент часу  . Набір значень
. Набір значень  незалежних змінних, не включаючи константу, позначимо через
незалежних змінних, не включаючи константу, позначимо через  . Лінійну модель можна записати у такому вигляді
. Лінійну модель можна записати у такому вигляді ,
,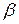 - вектор параметрів, які характеризують граничний ефект незалежних змінних на залежну. Це означає,що ефекти від зміни
- вектор параметрів, які характеризують граничний ефект незалежних змінних на залежну. Це означає,що ефекти від зміни  однакові для всіх одиниць в усіх спостереженнях є однаковими. Але середні змінні можуть змінюватись від одиниці до одиниці. Отже,
однакові для всіх одиниць в усіх спостереженнях є однаковими. Але середні змінні можуть змінюватись від одиниці до одиниці. Отже,  відображає дію факторів, які є специфічними від одиниці до одиниці, але не змінюються протягом часу. У стандартному випадку припускають, що
відображає дію факторів, які є специфічними від одиниці до одиниці, але не змінюються протягом часу. У стандартному випадку припускають, що  незалежні й однаково розподілені з нульовим середнім і дисперсією
незалежні й однаково розподілені з нульовим середнім і дисперсією  . Якщо
. Якщо 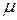 і дисперсією
і дисперсією  одержав назву моделі з випадковими ефектами. Тут важливим є припущення, що
одержав назву моделі з випадковими ефектами. Тут важливим є припущення, що  . Моделі з панельними даними дозволяють аналізувати зміни на індивідуальному рівні. Розглянемо ситуацію, коли середній рівень споживання зростає на 2 % щорічно, або, скажімо, тим, що приблизно збільшено споживання на 4%, а у решти рівень споживання змінився. Дослідження показали, що оцінювання за панельними даними є у більшості випадків більш ефективним, у порівнянні з ситуацією, коли доступний такиий самий обсяг даних, але дані утворюються в результаті вибору різних одиниць в кожний період часу. Моделі з панельними даними є більш стійкими по відношенню до пропущених змінних, похибок вимірювання та наявності ендогенних змінних серед регресорів.
. Моделі з панельними даними дозволяють аналізувати зміни на індивідуальному рівні. Розглянемо ситуацію, коли середній рівень споживання зростає на 2 % щорічно, або, скажімо, тим, що приблизно збільшено споживання на 4%, а у решти рівень споживання змінився. Дослідження показали, що оцінювання за панельними даними є у більшості випадків більш ефективним, у порівнянні з ситуацією, коли доступний такиий самий обсяг даних, але дані утворюються в результаті вибору різних одиниць в кожний період часу. Моделі з панельними даними є більш стійкими по відношенню до пропущених змінних, похибок вимірювання та наявності ендогенних змінних серед регресорів.


