
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ідея методу максимальної правдоподібностіСодержание книги
Поиск на нашем сайте Знаходження оцінок параметрів методом максимальної правдоподібністі (ММП) є одним з найбільш уживаних в економетриці завдяки оптимальним статистичним властивостям цих оцінок. Точне формулювання буде наведено нижче. Метод можна застосувати у тому випадку, коли розподіл спостережень відомий з точністю до скінченої кількості параметрів. Спочатку розглянемо знаходження ММП-оцінок у випадку незалежних виборок. Дискретний випадок Нехай y1,…, yn – незалежна виборка з дискретного розподілу, який задається набором можливих значень х1,…, хк та відповідних імовірностей
де
Останній вираз, якщо його розглянути як функцію від
Наприклад, якщо
де m-кількість одиниць серед чисел yi .. Оцінкою (методу) максимальної правдоподібності (ММП-оцінкою) називається таке значення Неперервний випадок. Нехай тепер
Нехай, наприклад
Як і Функція правдоподібності в економетричних моделях В економетричних моделях спостереження залежної змінної, взагалі кажучі, не є виборкою незалежних однаково розподілених випадкових величин. Тому для знаходження функції спільної щільності пропонується такий підхід. Спочатку слід знайти перетворення вихідної виборки, в результаті якого утворюється незалежна виборка, а потім застосувати формулу щільності для функції випадкових величин. Нехай
де Проілюструємо цей підхід на прикладах. Проста лінійна регресія. Нехай в моделі
збурення Перепишемо рівняння моделі в такому вигляді:
звідки
Таким чином, матриця перетворення є одиничною. Отже,
Ми показали, що функція правдоподібності має вигляд а її логарифм
Запишемо необхідну умову існування екстремуму:
Одержані рівняння називаються рівняннями максимальної правдоподібності. Якщо розписати ці рівняння, неважко побачити, що спочатку знаходяться розв’язки відносно
який є знайомою сумою квадратів залишків. Тобто ММП –оцінки параметрів регресії -
Процес АR(1). Нагадаємо, що модель має вигляд
де Отже,
Процес МА (1). Модель має вигляд
де Однак
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

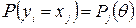 ,
, 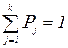 ,
, параметр, який потрібно оцінити. Припустимо, що
параметр, який потрібно оцінити. Припустимо, що 
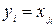 тоді
тоді 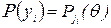 . Оскільки спостереження незалежні, то ймовірність даної реалізації виборки дорівнює
. Оскільки спостереження незалежні, то ймовірність даної реалізації виборки дорівнює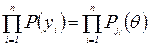 .
.
 – реалізація виборки з розподілу Бернулі з імовірністю успіху
– реалізація виборки з розподілу Бернулі з імовірністю успіху  то
то
 . Внаслідок незалежності функція спільної щільності дорівнює
. Внаслідок незалежності функція спільної щільності дорівнює  Остання функція, якщо її розглядати як функцію параметра називається функцією правдоподібності:
Остання функція, якщо її розглядати як функцію параметра називається функцією правдоподібності:
 - реалізація незалежної виборки з нормального розподілу з параметрами
- реалізація незалежної виборки з нормального розподілу з параметрами  і
і  . Тоді
. Тоді 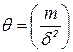 , а функція правдоподібності набуває вигляду
, а функція правдоподібності набуває вигляду =
=  .
. дискретному випадку, оцінки знаходяться з умови максимізації функції правдоподібності. Зауважимо, що оскільки функція правдоподібності є добутком, то технічно набагато простіше знаходити максимум її логарифму, який досягається при тих самих значеннях параметрів внаслідок монотонності логарифмічної функції
дискретному випадку, оцінки знаходяться з умови максимізації функції правдоподібності. Зауважимо, що оскільки функція правдоподібності є добутком, то технічно набагато простіше знаходити максимум її логарифму, який досягається при тих самих значеннях параметрів внаслідок монотонності логарифмічної функції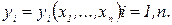 Якщо існують обернені функції
Якщо існують обернені функції  то
то
 – Якобіан перетворення
– Якобіан перетворення  .
.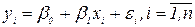
 незалежні і однаково розподілені (i.i.d) з розподілом
незалежні і однаково розподілені (i.i.d) з розподілом  . Тоді
. Тоді 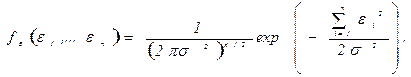
 ,
,
 , а
, а
 ,
,

 і
і  , а потім відносно
, а потім відносно  . Причому, знаходження розв’язку еквівалентно мінімізації виразу
. Причому, знаходження розв’язку еквівалентно мінімізації виразу ,
, і
і  незалежні. Другий підхід зручніше використовувати, якщо спостереження залежної змінної незалежні, а перший – якщо залежні.
незалежні. Другий підхід зручніше використовувати, якщо спостереження залежної змінної незалежні, а перший – якщо залежні. ,
, , а
, а  і мають розподіл
і мають розподіл  . Від
. Від  Зауважимо, що
Зауважимо, що  і
і 
 , тому Якобіан перетворення має вигляд
, тому Якобіан перетворення має вигляд  .
.
 ,
, і мають розподіл
і мають розподіл  В цьому випадку
В цьому випадку  .
. не спостерігається і не виражається через значення спостережень. Тому в цьому і подібних випадках використовують умовну функцію правдоподібності покладаючи
не спостерігається і не виражається через значення спостережень. Тому в цьому і подібних випадках використовують умовну функцію правдоподібності покладаючи  . Оскільки
. Оскільки 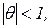 то
то  при
при  , а отже, умовна функція правдоподібності практично не відрізняється від точної функції правдоподібності. Якобіан перетворення також дорівнює 1, тому
, а отже, умовна функція правдоподібності практично не відрізняється від точної функції правдоподібності. Якобіан перетворення також дорівнює 1, тому .
.


