
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Три асимптотично еквівалентні критерії перевірки гіпотез.Содержание книги
Поиск на нашем сайте
1. Критерій відношення правдоподібності (LR). Нехай
асимптотично має розділ 2. Критерій Вальда. Запишемо гіпотезу про сукупність обмежень у такому вигляді
асимптотично має розподіл
де тобто
Кількість степенів свободи дорівнює кількості рядків в матриці R. Критерій можна застосувати не тільки для ММП-оцінок, але і для будь-яких консистентних асимптотично нормальних оцінок. Для перевірки гіпотези потрібно мати оцінки тільки в моделі без обмежень. Недоліком критерія є неінваріантність його статистики відносно форми запису обмежень. 3. Критерій множників Лагранжа (LM). Як і в попередньому випадку запишемо гіпотезу у вигляді.
асимптотично має розподіл Вибір критерія, як правило здійснюється з огляду на те, який з них простіше застосувати. Перевіряючи нелінійні обмеження, при можливості уникають використання критерія Вальда внаслідок його неінваріантності.
Дана модель запропонована Солоу. Коефіцієнти
де
Де На відміну від моделі з геометричним розподілом лагів, в якій коефіцієнти Для того, щоб записати модель з розподілом лагів Паскаля підставимо (2.45) до (2.35)
В моделі (2.47) невідомі параментри Вплив параметра
Рисунок 2.1 Модель з розподілом лагів Паскаля також можна записати у вигляді авторегресійної моделі. Згадаймо, що однію з основних переваг моделей з розподіленими лагами є можливість досліджувати розподіл в часі реакції залежної змінної на зміну визначальних факторів. Причиною уведення структур розподілів лагів, розглянутих нами, були такі недоліки моделей з необмеженими лагами як мультиколінеарність і необхідність визначення максимальної довжини лагу (надійність статистичних методів визначення максимальної довжини лагу також зменшується внаслідок мультиколінеарності). Проблема максимальної довжини лагу стосується і моделей з поліномільно розподіленими лагами. Моделі з геометричним розподілом лагів спираються на припущення, що величина реакції з самого початку монотонно спадає в часі. На практиці таке припущення виконується далеко не завжди. Наведемо такий тривіальний приклад. Припустимо, що ми використовуємо щомісячні дані, а максимальна реакція проявляє себе через 4 місяці. Зрозуміло, що в такому випадку найбільший коефіцієнт має бути при Yt-4. Таким чином, на нашу думку розподіл лагів Паскаля є найбільш гнучким засобом моделювання серед розглянутих нами, хоча, як ми побачимо у параграфі 6, в деяких випадках вигляд розподілу лагів можна вивести з економічних міркувань. У наступному підпараграфі ми розглянемо подальше узагальнення розподілу лагів Паскаля.
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 314; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.46.29 (0.006 с.) |

 -вектор параметрів моделі. Нехай гіпотеза
-вектор параметрів моделі. Нехай гіпотеза 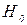 визначає сукупність обмеженнь на значення параметрів. Нехай
визначає сукупність обмеженнь на значення параметрів. Нехай  - ММП-оцінка, знайдена в моделі без обмежень,
- ММП-оцінка, знайдена в моделі без обмежень, 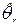 - ММП-оцінка, знайдена в моделі з обмеженням. Нехай
- ММП-оцінка, знайдена в моделі з обмеженням. Нехай  означають значення функцій правдоподібності для необмеженої і обмеженої моделей, знайдені в точках
означають значення функцій правдоподібності для необмеженої і обмеженої моделей, знайдені в точках  відповідно. При виконанні достатньо необмежливих умов регулярності статистика
відповідно. При виконанні достатньо необмежливих умов регулярності статистика
 - квадрат з кількістю степенів свободи, рівною кількості обмежень. Недоліком критерія є необхідність оцінювати модель в обох випадках – без обмежень і з обмеженнями.
- квадрат з кількістю степенів свободи, рівною кількості обмежень. Недоліком критерія є необхідність оцінювати модель в обох випадках – без обмежень і з обмеженнями.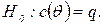 За умови, що обмеження вірні. Статистика Вальда
За умови, що обмеження вірні. Статистика Вальда .
. ). Зауважимо, що у випадку коли обмеження є нелінійними, то коваріаційну матрицю
). Зауважимо, що у випадку коли обмеження є нелінійними, то коваріаційну матрицю 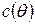 оцінюють наступним числом
оцінюють наступним числом ,
, ,
, рядок матриці С складають похідні
рядок матриці С складають похідні  обмеження відносно всіх елементів
обмеження відносно всіх елементів  . статистика Вальда набуває вигляду
. статистика Вальда набуває вигляду .
.
 2.5.2.Розподіл лагів Паскаля
2.5.2.Розподіл лагів Паскаля в основному рівнявнні (2.35) визначаються так
в основному рівнявнні (2.35) визначаються так для
для  , (2.45)
, (2.45)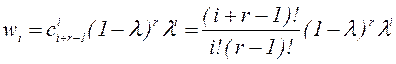 (2.46)
(2.46) - натуральне число,
- натуральне число,  .
. (2.47)
(2.47) . Зауважимо, що модель з геометрично розподіленими лагами є частковим випадком (2.47) при
. Зауважимо, що модель з геометрично розподіленими лагами є частковим випадком (2.47) при  .
. на характер розподілу лагів проілюстровано на рисунку 2.2, на якому зображено графік вагів для
на характер розподілу лагів проілюстровано на рисунку 2.2, на якому зображено графік вагів для 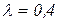 і
і  відповідно.
відповідно.



