
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перевірка значущості регресіїСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Значущість регресії означає, що незалежні змінні в сукупності впливають на залежну змінну. Як нульова гіпотеза для перевірки приймається протилежне тведження, а саме H0: b1=b2=...= b k- 1.= 0. Можна показати, що коли гіпотеза H0 вірна, то
За вибраним рівнем значущості a в таблиці розподілу Фішера з k– 1, n– 2 ступенями свободи знаходимо критичне значення F кр. Якщо | F |< F кр, то гіпотеза H0 приймається. Якщо | F |³ F кр, то гіпотеза H0 відхиляється. Прийняття нульової гіпотези означає, що модель потрібно відкинути і розглянути іншу.
1.2.7. Інтерпретація регресійних коефіцієнтів. Порівняння факторів за ступeнем їх впливу Запишемо рівняння регресії у такому вигляді:
Якщо значення змінної xi змінити на одиницю, а решту змінних залишити постійними, то, як зрозуміло з (2.25), значення Коефіцієнти рересійного рівняння було б заманливо використовувати для порівняння різних незалежних змінних (факторів) за ступенем їх впливу на залежну змінну. Однак тут виникають деякі проблеми. Зокрема, величина регресійних коефіцієнтів залежить від одиніці виміру. Припустимо, наприклад, що деяка змінна має грошовий вимір. Якщо значення цієї змінної перерахувати з купонокарбованців у гривні, то відповідний коефіцієнт збільшиться у сто тисяч разів. Крім того, одиниці виміру різних змінних в моделі можуть мати різний економічний зміст. Отже, регресійні коефіцієнти не можна використовувати для порівняння дії різних факторів. Найчастіше використовують два методи: 1. Порівняння коефіцієнтів в регресії відносно стандартизованих змінних. 2. Порівняння коефіцієнтів еластичності. Регресія відносно стандартизованих змінних. Розглянемо наступну модель лінійної регресії:
Введемо наступні позначення:
Модель регресії відносно стандартизованих змінних записується у такому вигляді:
Оскільки середні значення стандартизованих змінних дорівнюють нулю, то модель (1.55) не містить константи. Оцінки коефіцієнтів при стандартизованих змінних обчислюються за наступними формулами:
Зробимо такі зауваження. По-перше, оскільки середньоквадратичні відхилення мають ті самі розмірності, що і змінні, стандартизовані змінні є безрозмірними величинами. По-друге, середньоквадратичне відхилення можна інтерпретувати як типову для даної сукупності спостережень величину зміни змінної. Отже, можна сказати, що коефіцієнти стандартизованої регресії є мірою впливу незалежних змінних в термінах типової величини іх зміни. Коефіцієнти еластичності. Нехай змінна y залежить від змінних x 1,..., x k-1: y = f (x 1,..., x k-1). Коефіцієнт еластичності змінної y відносно xi визначається так:
Найчастіше використовують коефіцієнти еластичності попиту відносно ціни та доходу в моделях попиту. Коефіцієнт еластичності показує, на скільки відсотків зміниться y у відповідь на зміну xi у 1 відсоток за умови, що решта змінних залишиться постійною. Застосовуючи означення (1.56) до рівняння вибіркової регересії (1.36), одержимо формули для обчислення вибіркових коефіцієнтів еластичності
З формули (1.57) випливає, що коефіцієнти еластичності залежать від того, при якому значенні змінної вони обчислюються. Стандартним є обчислення коефіцієнтів еластичності при середніх значеннях змінних:
Відзначимо, що для порівняння не існує критерія, придатного в усіх ситуаціях. При виборі критерія треба враховувати мету дослідження, використовувати знання з тієї галузі економічної теоріїї, яка вивчає досліджуваний об’єкт. Наприклад, при аналізі виробничої функції можна робити порівняння коефіцієнтів еластичності відносно праці та капіталу з урахуванням вартості зміни на один відсоток величини капіталу та обсягу трудових ресурсів.
1.2.8.Моделі, які зводяться до моделі лінійної регресії Розглянемо виробничу функцію Коба–Дугласа: Y = AL a C b, (1.59) де Y –валовий випуск, L– обсяг трудових ресурсів, С –обсяг капіталу (виробничих фондів), A, a, b – параметри. Коефіцієнт пропорційності A відображає рівень технології. Парамери a та b є коефіцієнтами еластичності відносно праці та капіталу (отже, функція Коба–Дугласа є виробничою функцією зі сталою еластичністю). Прологарифмувавши рівняння (1.59), маємо: y = a + a l + b c, (1.60) де a = ln A, l = ln L, c = ln C. Якщо ввести до рівняння (1.60) стохастичний доданок, то одержимо модель лінійної регресії: y = a + a l + b c +e. (1.61) Щоб перетворити вихідну модель (1.59) на стохастичну, обчислимо експоненту від обох частин рівності (1.61): Y = AL a C bee. (1.62) Ми бачимо, що модель (1.62) можна звести до моделі лінійної регресіі. Аналогічно можна вивчати досить широкий клас моделей, які за допомогою перетворень змінних та рівнянь можна звести до моделі лінійної регресії. Широковживаним є приклад поліноміальної регресії:
1 .2.9. Фіктивні змінні. У попередніх розділах ми розглядали змінні, які можна вимірювати за допомогою кількісних шкал (вартість капіталу, рівень інфляції, обсяг попиту і т.ін.). Однак, у багатьох випадках на поведінку змінної, яку ми вивчаємо впливають якісні фактори, наприклад, наявність або відсутність вищої освіти, статеві, расові відмінності. Для врахування дії подібних чинників застосовують фіктивні змінні. Фіктивні, або бінарні змінні можуть приймати два значення: 0 та 1. Розглянемо декілька прикладів. Нехай ми вивчаємо залежність заробітної платні від віку та рівня освіти за допомогою такої моделі
де y – величина зарплатні, x1 – вік у роках, x2 – рівень освіти, який вимірюється у роках навчання. Припустимо, що нам потрібно виявити, чи існує відмінність в оплаті праці між чоловіками і жінками. Для цього ми утворюємо фіктивну змінну D: D = 1 для чоловіків і D = 0 для жінок. Модель набуде вигляду
Величина коефіціента b3 показує відмінність у седньому рівні заробітної платні між чоловіками і жінками, які мають однаковий вік та рівень освіти. Для того, щоб відтворити в моделі вплив якісного фактора, який може приймати m рівнів, в модель потрібно включити m –1 фіктивну змінну. Розглянемо модель, яка вивчає ринкову вартість квадратного метра житла:
На ціну квадратного метра житлової площі впливає, на якому поверсі знаходиться квартира, причому важливо, чи є поверх першим, останнім, або ні першим, ні останнім. Тобто фактор «поверх» приймає три значення. Отже, ми формуємо дві фіктивні змінні D1 і D2:
Тепер модель має вигляд
За такого вибору фіктивних змінних середня ціна квадратного метра квартири, розташованої на «середньому» поверсі є базовою. За умови рівності змінних (факторів) x 1,..., x k-1 середня ціна квадратного метра квартири, розташованої на першому поверсі відрізняється від базового рівня на величину g1, а квартири, розташованої на останньому поверсі – на величину g2. Фіктивні змінні також використовують для врахування cезонного ефекту. Наприклад, залежність між змінними x та y на основі щоквартальних даних можна досліджувати за допомогою такої моделі: y= a + b x + g1 D 1 + g2 D 2 + g3 D 3 + e, (1.63) де D 1, D 2, та D 3 – сезонні фіктивні змінні, які визначаються наступним чином:
При наявності щомісячних даних використовують 11 сезонних фіктивних змінних:
...
1 .2.10.Перевірка гіпотез про лінійні обмеження на параметри В параграфі 1.2.6 ми побачили, як перевіряти гіпотези про окремо взяті регресійні коефіціенти. Однак, часто з економічних міркувань випливають більш складні обмеження на параметри регресії. Розглянемо кілька прикладів. Неважко показати, що економічна система, яка описується функцією Коба–Дугласа (1.59) має нейтральний ефект від масштабу (ресурси мають постійну ефективність), якщо a +b = 1, негативний ефект від масштабу (ресурси мають спадну ефективність), якщо a +b < 1 і позитивний ефект від масштабу (ресурси мають зростаючу ефективність), якщо a +b > 1. Постає питання: чи в даній економічній системі має місце нейтральний ефект від масштабу? Щоб відповісти на це питання, потрібно в моделі лінійної регресії (1.61) перевірити гіпотезу H0: a +b = 1. (1.64) Гіпотеза (1.64) є прикладом гіпотези про лінійне обмеження на параметри регресії, яка у загальному випадку записується так:
Нерідко виникає потреба перевірити гіпотезу про те, що кілька лінійних обмежень виконуються водночас, іншими словами, гіпотезу про сукупність лінійних обмежень. Так, відсутність сезонного ефекту в моделі (1.63) означає, що коефіціенти при сезонних фіктивних змінних дорівнюють нулю водночас. Отже перевірка твердження про відсутність сезонного ефекту зводиться до перевірки наступної гіпотези: H0:
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 570; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.200.151 (0.012 с.) |

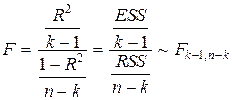 (1.52)
(1.52)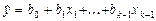 (1.53).
(1.53).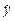 зміниться на bi одиниць. Таким чином, коефіцієнти регресійного рівняння є кількісною мірою впливу окремо взятих незалежних змінних на залежну змінну за умови ceteris paribus.
зміниться на bi одиниць. Таким чином, коефіцієнти регресійного рівняння є кількісною мірою впливу окремо взятих незалежних змінних на залежну змінну за умови ceteris paribus. (1.54).
(1.54).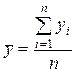 –середнє значення залежної змінної,
–середнє значення залежної змінної,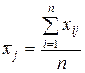 ,
, 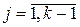 – середнє значення j -ї незалежної змінної,
– середнє значення j -ї незалежної змінної,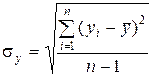 –середньоквадратичне відхилення залежної змінної,
–середньоквадратичне відхилення залежної змінної,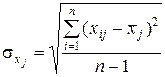 ,
, 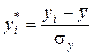 ,
, 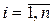 –значення стандартизованої залежної змінної в i -му спостереженні
–значення стандартизованої залежної змінної в i -му спостереженні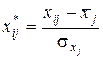 ,
, 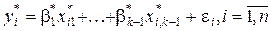 . (1.55)
. (1.55) ,
, 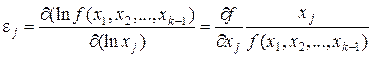 ,
, 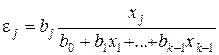 ,
, 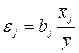 ,
, 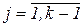 (1.58)
(1.58) .
. ,
,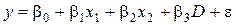 .
. .
.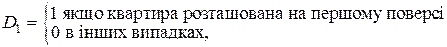
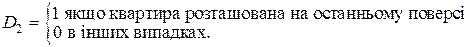
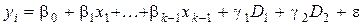 .
.

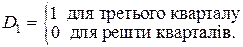
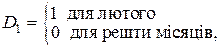
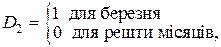
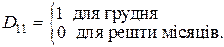
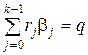 , де rj,
, де rj, 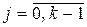 та q – відомі числа,
та q – відомі числа,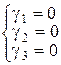 .
.


