
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистична і кореляційна залежність. Функції та лінії регресіїСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Показником, що вимірює стохастичний зв’язок між змінними, є коефіцієнт кореляції, який свідчить з певною мірою ймовірності, наскільки зв’язок між змінними близький до строгої лінійної залежності. За наявності кореляційного зв’язку між змінними необхідно виявити його форму функціональної залежності (лінійна чи нелінійна), а саме:
Наведені можливі залежності між змінними X і Y називають функціями регресії. Форму зв’язку між змінними X і Y можна встановити, застосовуючи кореляційні поля, які зображені на рисунках Для двовимірного статистичного розподілу вибірки ознак (Х, Y) поняття статистичної залежності між ознаками Х та Y має таке визначення: статистичною залежністю Х від Y називають таку, за якої при зміні значень ознаки Y = yi змінюється умовний статистичний розподіл ознаки Х, статистичною залежністю ознаки Y від Х називають таку, за якої зі зміною значень ознаки X = xi змінюється умовний статистичний розподіл ознаки Y. Між ознаками Х та Y може існувати статистична залежність і за відсутності кореляційної. Але коли існує кореляційна залежність між ознаками Х та Y, то обов’язково між ними існуватиме і статистична залежність Парна лінійна регресія. Вибірковий коефіцієнт кореляції та його властивості Ураховуючи вплив на значення Y збурювальних випадкових факторів, лінійне рівняння зв’язку X і Y можна подати в такому вигляді:
де Отже, в рівнянні (485) значення «y» подається у вигляді суми двох частин: систематичної У результаті статистичних спостережень дослідник дістає характеристики для незалежної змінної х і відповідні значення залежної змінної у. Вибірковий коефіцієнт кореляції Рівняння лінійної парної регресії:
де
Як бачимо, коефіцієнт кореляції близький за своїм значенням до одиниці, що свідчить про те, що залежність між Х та Y є практично лінійною
Надійний інтервал для лінійної регресії Ураховуючи те, що
Тоді
Звідси дістали:
має t- розподіл із
випливає
Лінійна регресія для двовимірного статистичного розподілу Ураховуючи вплив на значення Y збурювальних випадкових факторів, лінійне рівняння зв’язку X і Y можна подати в такому вигляді:
де Отже, в рівнянні (485) значення «y» подається у вигляді суми двох частин: систематичної У результаті статистичних спостережень дослідник дістає характеристики для незалежної змінної х і відповідні значення залежної змінної Множинна лінійна регресія На практиці здебільшого залежна змінна Довірчий інтервал для множинної лінійної регресії Матриця Х містить m лінійно незалежних векторів-стовпців, а це означає, що ранг її дорівнюватиме m і визначник Дисперсії статистичних оцінок Коефіцієнт множинної регресії Тісноту між ознаками Y та X, де
Чим ближче значення R до ±1, тим краще вибрано функцію регресії Нормування коефіцієнтів регресії Множинна лінійна регресія дає змогу порівняти вплив на досліджуваний процес різних чинників. У загальному випадку змінні
де
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 618; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.166.217 (0.01 с.) |

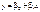 ;
; ;
;
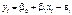 ,
, ,
, 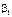 є невідомі параметри регресії,
є невідомі параметри регресії, 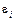 є випадковою змінною, що характеризує відхилення y від гіпотетичної теоретичної регресії.
є випадковою змінною, що характеризує відхилення y від гіпотетичної теоретичної регресії. і випадкової
і випадкової  . Параметри
. Параметри  ,
,  є невідомими величинами, а
є невідомими величинами, а  ,
,  . При цьому елементи послідовності
. При цьому елементи послідовності  є некорельованими
є некорельованими 
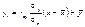 або
або ,
, і називають коефіцієнтом регресії. Для обчислення
і називають коефіцієнтом регресії. Для обчислення  необхідно знайти
необхідно знайти 


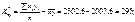
 ;
;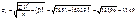 ;
;
 і
і  є випадковими величинами, то і лінійна функція регресії
є випадковими величинами, то і лінійна функція регресії 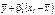 буде випадковою. Позначимо через
буде випадковою. Позначимо через  значення ознаки Y, обчислимо за формулою
значення ознаки Y, обчислимо за формулою .
.




 .
.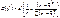 або
або .Випадкова величина
.Випадкова величина
 ступенями свободи. Ураховуючи можна побудувати довірчий інтервал для лінійної парної функції регресії із заданою надійністю γ, а саме:
ступенями свободи. Ураховуючи можна побудувати довірчий інтервал для лінійної парної функції регресії із заданою надійністю γ, а саме: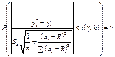 .
.
 пов’язана з впливом не одного, а кількох аргументів.
пов’язана з впливом не одного, а кількох аргументів.  Отже, матриця
Отже, матриця  має обернену.
має обернену. визначають з допомогою кореляційної матриці для вектора
визначають з допомогою кореляційної матриці для вектора , вимірюють з допомогою коефіцієнта множинної кореляції R, що є узагальненням парного коефіцієнта кореляції rij і обчислюється за формулою
, вимірюють з допомогою коефіцієнта множинної кореляції R, що є узагальненням парного коефіцієнта кореляції rij і обчислюється за формулою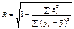 .
. репрезентують чинники, що мають різні одиниці виміру (кілограми, гривні, метри тощо). Отже, для того щоб порівняти і з’ясувати відносну вагомість кожного з чинників, використовують так звані нормовані коефіцієнти регресії, які визначають за формулою
репрезентують чинники, що мають різні одиниці виміру (кілограми, гривні, метри тощо). Отже, для того щоб порівняти і з’ясувати відносну вагомість кожного з чинників, використовують так звані нормовані коефіцієнти регресії, які визначають за формулою
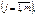
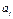 — коефіцієнт регресії після нормування;
— коефіцієнт регресії після нормування;  — виправлене середнє квадратичне відхилення змінної
— виправлене середнє квадратичне відхилення змінної 
 — виправлене середнє квадратичне відхилення ознаки Y.
— виправлене середнє квадратичне відхилення ознаки Y.


