
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремадодавання ймовірностей двох несумісних подійСодержание книги
Поиск на нашем сайте Залежні та незалежні події. Умовна ймовірність Події В і С називаються залежними, якщо ймовірність однієї з них змінюється залежно від того, відбулась друга подія чи ні. У противному разі події називаються незалежними Умовна ймовірність та її властивості. Імовірність події A, визначена за умови, що подія В відбулася, називається умовною і позначається P(A/B). P(A/B)= P(AB) / P(B), P(B) P(A/B)=0, якщо = 1. P(A/B)=1, якщо =B 2. у решті випадків 0<P(A/B)<1. Теорема множення ймовірностей двох незалежних подій. Наслідок Ймовірність появи хоча б однієї події Теорема множення ймовірностей двох залежних подій. Наслідок Теорема додавання ймовірностей двох сумісних подій Формула повної ймовірності Нехай подія А може відбутися тільки за умови настання однієї із несумісних подій
де Наведена залежність називається формулою повної ймовірності. Формула Баєса Подія А може відбутись одночасно з деякою із подій
Формула Бернуллі Імовірність того, що в n незалежних випробуваннях, у кожному з яких імовірність Р (А) = р, подія А відбудеться m раз, подається так:
Імовірність того, що в результаті n незалежних експериментів подія А з’явиться від mi до mj раз, обчислюється так: Локальна теорема Лапласа Імовірність того, що в n незалежних випробуваннях, у кожному з яких Р (А) = р, подія А відбудеться m раз, подається такою наближеною залежністю:
Локальна теорема Лапласа дає змогу обчислювати ймовірності Інтегральна теорема Лапласа Імовірність того, що подія А відбудеться від
Значення функції Лапласа наводяться у спеціальних таблицях. Найвірогідніше число появи події в n-випробуваннях Імовірність того, що в n незалежних випробуваннях, у кожному з яких імовірність Р (А) = р, подія А відбудеться m раз, подається так:
Імовірність того, що в результаті n незалежних експериментів подія А з’явиться від mi до mj раз, обчислюється так: Випадкові величини. Дискретні та неперервні випадкові величини Випадковою називається величина, яка може набувати різних числових значень. Строгіше означення випадкової величини пов’язане з поняттям простору елементарних подій. Нехай задано простір елементарних подій W. Однозначна числова функція Закон розподілу ймовірностей дискретної випадкової величини. Функція розподілу Співвідношення між значеннями випадкової величини і їхніми ймовірностями називається законом розподілу випадкової величини. Для дискретних випадкових величин закони розподілу можуть задаватися множиною значень, що їх набуває випадкова величина, і ймовірностями цих значень. Якщо Функція розподілу — неспадна, неперервна зліва, Для довільних
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.005 с.) |

 0. Властивості умовної ймовірності:
0. Властивості умовної ймовірності: (i = 1, 2,…, n), які утворюють повну групу. Тоді ймовірність події А подається формулою:
(i = 1, 2,…, n), які утворюють повну групу. Тоді ймовірність події А подається формулою:
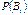 — імовірність події
— імовірність події 
 — умовні ймовірності настання події А.
— умовні ймовірності настання події А. Відомі ймовірності подій
Відомі ймовірності подій  та умовні ймовірності того, що подія А відбудеться. Відомо, що в результаті випробування подія А відбулась. Потрібно з огляду на це переоцінити ймовірності гіпотез
та умовні ймовірності того, що подія А відбудеться. Відомо, що в результаті випробування подія А відбулась. Потрібно з огляду на це переоцінити ймовірності гіпотез  Для цього застосовують формулу Баєса:
Для цього застосовують формулу Баєса:
 Формула застосовується, якщо
Формула застосовується, якщо 



 , якщо n > 10 i p > 0,1.
, якщо n > 10 i p > 0,1. до
до  раз при проведенні n незалежних випробувань, у кожному з яких подія А відбувається з імовірністю р, подається формулою:
раз при проведенні n незалежних випробувань, у кожному з яких подія А відбувається з імовірністю р, подається формулою: —функція Лапласа;
—функція Лапласа;

 яку задано на просторі елементарних подій, називається випадковою величиною. Якщо простір W дискретний, то випадкова величина дискретна. Неперервному простору елементарних подій відповідає неперервна випадкова величина.
яку задано на просторі елементарних подій, називається випадковою величиною. Якщо простір W дискретний, то випадкова величина дискретна. Неперервному простору елементарних подій відповідає неперервна випадкова величина. то
то  або, якщо величина набуває зліченної множини значень, то
або, якщо величина набуває зліченної множини значень, то  Закони розподілу дискретних випадкових величин задаються у табличній формі (подаються значення випадкової величини і їхні ймовірності), аналітичній (наводиться формула, за якою обчислюються ймовірності для заданих значень випадкової величини), графічній (у прямокутній системі координат задається набір точок
Закони розподілу дискретних випадкових величин задаються у табличній формі (подаються значення випадкової величини і їхні ймовірності), аналітичній (наводиться формула, за якою обчислюються ймовірності для заданих значень випадкової величини), графічній (у прямокутній системі координат задається набір точок 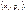 сполучивши точки відрізками прямих, дістанемо многокутник розподілу ймовірностей). Універсальним способом задання закону розподілу ймовірностей є функція розподілу
сполучивши точки відрізками прямих, дістанемо многокутник розподілу ймовірностей). Універсальним способом задання закону розподілу ймовірностей є функція розподілу 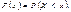 Цю функцію можна тлумачити так:унаслідок експерименту випадкова величина може набути значення,меншого за х. Для дискретних величин
Цю функцію можна тлумачити так:унаслідок експерименту випадкова величина може набути значення,меншого за х. Для дискретних величин 







