
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Класичне і геометричне означення ймовірностіСодержание книги
Поиск на нашем сайте
Класичне і геометричне означення ймовірності Класичною імовірністю випадкової події А називається відношення кількості елементарних подій m, які сприяють появі цієї події (становлять множину її елементарних подій), до загальної кількості n рівноможливих елементарних подій, що утворюють простір елементарних подій W: P(A)= m /n. Переставленням із n елементів називають такі впорядковані множини з n елементів, які різняться між собою порядком їх розміщення. Кількість таких упорядкованих множин обчислюється за формулою: Pn = n! Розміщенням із n елементів по m (0 Комбінаціями з n елементів по m (0 Статистичною ймовірністю події А називається відношення кількості m випробувань, в яких подія А відбулась, до загальної кількості виконаних випробувань n: W(A)= m /n. Знаходження статистичної ймовірності пов’язане з проведенням n випробувань, тому вона називається ще частістю, або відносною частотою, події. Алгебра подій Система подій називається алгеброю подій, якщо: 1. 2. із того, що Числова функція P, що визначена на системі подій Q, називається ймовірністю, якщо: 1. Q є алгеброю подій; 2. для будь-якого A Ì Q існує P(A)³0; 3. P(W)= 1; 4. якщо А і В є несумісними (АÇВ)=Æ, то P(AÈB)=P(A)+P(B); 5. для будь-якої спадної послідовності
Q,
Трійка (Q,W,R), де Q є алгеброю подій і Р задовольняє аксіоми 1-5, називається простором імовірностей. Теоремадодавання ймовірностей двох несумісних подій Залежні та незалежні події. Умовна ймовірність Події В і С називаються залежними, якщо ймовірність однієї з них змінюється залежно від того, відбулась друга подія чи ні. У противному разі події називаються незалежними Умовна ймовірність та її властивості. Імовірність події A, визначена за умови, що подія В відбулася, називається умовною і позначається P(A/B). P(A/B)= P(AB) / P(B), P(B) P(A/B)=0, якщо = 1. P(A/B)=1, якщо =B 2. у решті випадків 0<P(A/B)<1. Теорема множення ймовірностей двох незалежних подій. Наслідок Ймовірність появи хоча б однієї події Теорема множення ймовірностей двох залежних подій. Наслідок Теорема додавання ймовірностей двох сумісних подій Формула повної ймовірності Нехай подія А може відбутися тільки за умови настання однієї із несумісних подій
де Наведена залежність називається формулою повної ймовірності. Формула Баєса Подія А може відбутись одночасно з деякою із подій
Формула Бернуллі Імовірність того, що в n незалежних випробуваннях, у кожному з яких імовірність Р (А) = р, подія А відбудеться m раз, подається так:
Імовірність того, що в результаті n незалежних експериментів подія А з’явиться від mi до mj раз, обчислюється так: Локальна теорема Лапласа Імовірність того, що в n незалежних випробуваннях, у кожному з яких Р (А) = р, подія А відбудеться m раз, подається такою наближеною залежністю:
Локальна теорема Лапласа дає змогу обчислювати ймовірності Інтегральна теорема Лапласа Імовірність того, що подія А відбудеться від
Значення функції Лапласа наводяться у спеціальних таблицях. Закон розподілу ймовірностей дискретної випадкової величини. Функція розподілу Співвідношення між значеннями випадкової величини і їхніми ймовірностями називається законом розподілу випадкової величини. Для дискретних випадкових величин закони розподілу можуть задаватися множиною значень, що їх набуває випадкова величина, і ймовірностями цих значень. Якщо Функція розподілу — неспадна, неперервна зліва, Для довільних Розподіл Пуассона Дискретна випадкова величина має розподіл Пуассона, якщо вона набуває зліченної множини значень Якщо у схемі незалежних повторних випробувань n велике і р або 1 – р прямують до нуля, то біноміальний розподіл апроксимується розподілом Пуассона, коли Ймовірна твірна Теорема Чебишова Нехай 1.M(Xі)>= aі 2.D(Xі )<= с Для всіх і=1,2,3…..n Якщо випадкові величини у послідовності Ця теорема є законом великих чисел,так само як і центральна гранична теорема Теорема Бернулі Нехай проводиться n незалежних повторних випробувань, у кожному з яких імовірність настання події А дорівнює р.Якщо ймовірність появи випадкової події А в кожному з незалежних випробувань n є величиною сталою і дорівнює P,то при необмеженому збільшенні числа експериментів n→∞ Імовірність відхилення відносної частоти появи випадкової події W(A) від імовірності p,взятої за абсолютною величиною на ε(ε>0) прямуватиме до одиниці зі зростанням n,що можна записати так:
де Наведена теорема є законом великих чисел,так само як і центральна гранична теорема Загальна схема перевірки статистичних гіпотез. Перевірка достовірності гіпотез про частку ознаки генеральної сукупності, про рівність частот ознаки двох вибірок, про значення генеральної середньої, про рівність двох генеральних середніх і дисперсій Перевірка правельності нульової гіпотези про нормальний закон розподілу ознаки генеральної сукупності Для перевірки правильності Н 0 задається так званий рівень значущості a. a — це мала ймовірність, якою наперед задаються. Вона може набувати значення a = 0,005; 0,01; 0,001. В основу перевірки Н 0 покладено принцип 1. Сформулювати Н 0 й одночасно альтернативну гіпотезу Н a. 2. Вибрати статистичний критерій, який відповідав би сформульованій нульовій гіпотезі. 3. Залежно від змісту нульової та альтернативної гіпотез будується правобічна, лівобічна або двобічна критична область, а саме: нехай
4. Для побудови критичної області (лівобічної, правобічної чи двобічної) необхідно знайти критичні точки. За вибраним статистичним критерієм та рівнем значущості a знаходяться критичні точки. 5. За результатами вибірки обчислюється спостережуване значення критерію 6. Відхиляють чи приймають нульову гіпотезу на підставі таких міркувань: у разі, коли для двобічної критичної області або Множинна лінійна регресія На практиці здебільшого залежна змінна Довірчий інтервал для множинної лінійної регресії Матриця Х містить m лінійно незалежних векторів-стовпців, а це означає, що ранг її дорівнюватиме m і визначник Дисперсії статистичних оцінок Коефіцієнт множинної регресії Тісноту між ознаками Y та X, де
Чим ближче значення R до ±1, тим краще вибрано функцію регресії Нормування коефіцієнтів регресії Множинна лінійна регресія дає змогу порівняти вплив на досліджуваний процес різних чинників. У загальному випадку змінні
де Класичне і геометричне означення ймовірності Класичною імовірністю випадкової події А називається відношення кількості елементарних подій m, які сприяють появі цієї події (становлять множину її елементарних подій), до загальної кількості n рівноможливих елементарних подій, що утворюють простір елементарних подій W: P(A)= m /n. Переставленням із n елементів називають такі впорядковані множини з n елементів, які різняться між собою порядком їх розміщення. Кількість таких упорядкованих множин обчислюється за формулою: Pn = n! Розміщенням із n елементів по m (0 Комбінаціями з n елементів по m (0 Статистичною ймовірністю події А називається відношення кількості m випробувань, в яких подія А відбулась, до загальної кількості виконаних випробувань n: W(A)= m /n. Знаходження статистичної ймовірності пов’язане з проведенням n випробувань, тому вона називається ще частістю, або відносною частотою, події. Алгебра подій Система подій називається алгеброю подій, якщо: 1. 2. із того, що Числова функція P, що визначена на системі подій Q, називається ймовірністю, якщо: 1. Q є алгеброю подій; 2. для будь-якого A Ì Q існує P(A)³0; 3. P(W)= 1; 4. якщо А і В є несумісними (АÇВ)=Æ, то P(AÈB)=P(A)+P(B); 5. для будь-якої спадної послідовності
Q,
Трійка (Q,W,R), де Q є алгеброю подій і Р задовольняє аксіоми 1-5, називається простором імовірностей.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 674; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.142.215 (0.007 с.) |

 m
m  = n! /(n-m)!
= n! /(n-m)! = n! / m!(n-m)! Геометричне означення ймовірності. Якщо простір елементарних подій W можна подати у вигляді деякого геометричного предмета, а множину елементарних подій для подій А – як частину цього геометричного образу, то ймовірність події А визначається як відношення мір цих множин P(A)=m(A)/m(W).При цьому вважається, що попадання в деяку частину геометричного образу пропорційна до міри цієї його частини.
= n! / m!(n-m)! Геометричне означення ймовірності. Якщо простір елементарних подій W можна подати у вигляді деякого геометричного предмета, а множину елементарних подій для подій А – як частину цього геометричного образу, то ймовірність події А визначається як відношення мір цих множин P(A)=m(A)/m(W).При цьому вважається, що попадання в деяку частину геометричного образу пропорційна до міри цієї його частини.
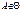 ,
,  випливає, що:
випливає, що:  ,
,  ,
, 
 подій із Q, такої, що
подій із Q, такої, що випливає рівність
випливає рівність 0. Властивості умовної ймовірності:
0. Властивості умовної ймовірності: (i = 1, 2,…, n), які утворюють повну групу. Тоді ймовірність події А подається формулою:
(i = 1, 2,…, n), які утворюють повну групу. Тоді ймовірність події А подається формулою:
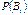 — імовірність події
— імовірність події 
 — умовні ймовірності настання події А.
— умовні ймовірності настання події А. Відомі ймовірності подій
Відомі ймовірності подій  та умовні ймовірності того, що подія А відбудеться. Відомо, що в результаті випробування подія А відбулась. Потрібно з огляду на це переоцінити ймовірності гіпотез
та умовні ймовірності того, що подія А відбудеться. Відомо, що в результаті випробування подія А відбулась. Потрібно з огляду на це переоцінити ймовірності гіпотез  Для цього застосовують формулу Баєса:
Для цього застосовують формулу Баєса:
 Формула застосовується, якщо
Формула застосовується, якщо 



 , якщо n > 10 i p > 0,1.
, якщо n > 10 i p > 0,1. до
до  раз при проведенні n незалежних випробувань, у кожному з яких подія А відбувається з імовірністю р, подається формулою:
раз при проведенні n незалежних випробувань, у кожному з яких подія А відбувається з імовірністю р, подається формулою: —функція Лапласа;
—функція Лапласа;

 то
то  або, якщо величина набуває зліченної множини значень, то
або, якщо величина набуває зліченної множини значень, то  Закони розподілу дискретних випадкових величин задаються у табличній формі (подаються значення випадкової величини і їхні ймовірності), аналітичній (наводиться формула, за якою обчислюються ймовірності для заданих значень випадкової величини), графічній (у прямокутній системі координат задається набір точок
Закони розподілу дискретних випадкових величин задаються у табличній формі (подаються значення випадкової величини і їхні ймовірності), аналітичній (наводиться формула, за якою обчислюються ймовірності для заданих значень випадкової величини), графічній (у прямокутній системі координат задається набір точок 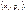 сполучивши точки відрізками прямих, дістанемо многокутник розподілу ймовірностей). Універсальним способом задання закону розподілу ймовірностей є функція розподілу
сполучивши точки відрізками прямих, дістанемо многокутник розподілу ймовірностей). Універсальним способом задання закону розподілу ймовірностей є функція розподілу 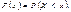 Цю функцію можна тлумачити так:унаслідок експерименту випадкова величина може набути значення,меншого за х. Для дискретних величин
Цю функцію можна тлумачити так:унаслідок експерименту випадкова величина може набути значення,меншого за х. Для дискретних величин 




 з імовірностями
з імовірностями 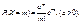 Цей розподіл описує кількість подій, які настають в однакові проміжки часу за умови, що ці події відбуваються незалежно одна від одної зі сталою інтенсивністю. Розподіл Пуассона розглядається як статистична модель для кількості альфа-частинок, що їх випромінює радіоактивне джерело за певний проміжок часу; кількості викликів, які надходять на телефонну станцію за певний період доби; кількості вимог щодо виплати страхових сум за рік; кількості дефектів на однакових пробах речовини і т. ін. Розподіл застосовується в задачах статистичного контролю якості, у теорії надійності, теорії масового обслуговування. Математичне сподівання і дисперсія в цьому розподілі однакові і дорівнюють а. Для цього розподілу складено таблиці щодо різних значень
Цей розподіл описує кількість подій, які настають в однакові проміжки часу за умови, що ці події відбуваються незалежно одна від одної зі сталою інтенсивністю. Розподіл Пуассона розглядається як статистична модель для кількості альфа-частинок, що їх випромінює радіоактивне джерело за певний проміжок часу; кількості викликів, які надходять на телефонну станцію за певний період доби; кількості вимог щодо виплати страхових сум за рік; кількості дефектів на однакових пробах речовини і т. ін. Розподіл застосовується в задачах статистичного контролю якості, у теорії надійності, теорії масового обслуговування. Математичне сподівання і дисперсія в цьому розподілі однакові і дорівнюють а. Для цього розподілу складено таблиці щодо різних значень  (0,1 – 20). У таблицях для відповідних значень а наведено ймовірності
(0,1 – 20). У таблицях для відповідних значень а наведено ймовірності 
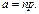

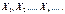 послідовність незалежних випадкових величин,які задовольняють умовам:
послідовність незалежних випадкових величин,які задовольняють умовам: незалежні, мають скінченні математичні сподівання і рівномірно обмежені дисперсії
незалежні, мають скінченні математичні сподівання і рівномірно обмежені дисперсії 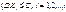 , то до послідовності (1) можна застосувати закон великих чисел. Це означає що середне арифметичне достатньо великої кількості незалежних випадкових величин дуже мало відрізняється від середнього арифметичного їхніх математичних сподівань,взятого за абсолютним значенням.
, то до послідовності (1) можна застосувати закон великих чисел. Це означає що середне арифметичне достатньо великої кількості незалежних випадкових величин дуже мало відрізняється від середнього арифметичного їхніх математичних сподівань,взятого за абсолютним значенням.
 — частота події А у даних випробуваннях. Таким чином при необмеженому збільшенні числа незалежних випробувань за схемою Бернулі відносна частота дуже мало відрізняється від ймовірності.
— частота події А у даних випробуваннях. Таким чином при необмеженому збільшенні числа незалежних випробувань за схемою Бернулі відносна частота дуже мало відрізняється від ймовірності. , тобто ймовірність того, що статистичний критерій потрапляє в критичну область
, тобто ймовірність того, що статистичний критерій потрапляє в критичну область  , дорівнює малій імовірності a. Якщо ж виявиться, що
, дорівнює малій імовірності a. Якщо ж виявиться, що 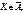 а ця подія малоймовірна і все ж відбулася, то немає підстав приймати нульову гіпотезу. Пропонується такий алгоритм перевірки правильності Н 0:
а ця подія малоймовірна і все ж відбулася, то немає підстав приймати нульову гіпотезу. Пропонується такий алгоритм перевірки правильності Н 0: , тоді, якщо
, тоді, якщо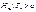 , то вибирається правобічна критична область, якщо
, то вибирається правобічна критична область, якщо , то вибирається лівобічна критична область і коли
, то вибирається лівобічна критична область і коли , то вибирається двобічна критична область.
, то вибирається двобічна критична область. .
.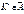 , а це є малоймовірною випадковою подією,
, а це є малоймовірною випадковою подією,  і, незважаючи на це, вона відбулася, то в цьому разі Н 0 відхиляється: для лівобічної критичної області
і, незважаючи на це, вона відбулася, то в цьому разі Н 0 відхиляється: для лівобічної критичної області  ; для правобічної критичної області
; для правобічної критичної області 
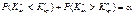
 , ураховуючи ту обставину, що критичні точки
, ураховуючи ту обставину, що критичні точки  і
і  симетрично розташовані відносно нуля.
симетрично розташовані відносно нуля. пов’язана з впливом не одного, а кількох аргументів.
пов’язана з впливом не одного, а кількох аргументів.  Отже, матриця
Отже, матриця  має обернену.
має обернену. визначають з допомогою кореляційної матриці для вектора
визначають з допомогою кореляційної матриці для вектора , вимірюють з допомогою коефіцієнта множинної кореляції R, що є узагальненням парного коефіцієнта кореляції rij і обчислюється за формулою
, вимірюють з допомогою коефіцієнта множинної кореляції R, що є узагальненням парного коефіцієнта кореляції rij і обчислюється за формулою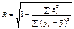 .
. репрезентують чинники, що мають різні одиниці виміру (кілограми, гривні, метри тощо). Отже, для того щоб порівняти і з’ясувати відносну вагомість кожного з чинників, використовують так звані нормовані коефіцієнти регресії, які визначають за формулою
репрезентують чинники, що мають різні одиниці виміру (кілограми, гривні, метри тощо). Отже, для того щоб порівняти і з’ясувати відносну вагомість кожного з чинників, використовують так звані нормовані коефіцієнти регресії, які визначають за формулою
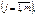
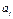 — коефіцієнт регресії після нормування;
— коефіцієнт регресії після нормування;  — виправлене середнє квадратичне відхилення змінної
— виправлене середнє квадратичне відхилення змінної 
 — виправлене середнє квадратичне відхилення ознаки Y.
— виправлене середнє квадратичне відхилення ознаки Y.


