
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистичний розподіл вибірки. Полігон частот і гістограма. Кумулята. Емпірична функція розподілуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дискретний статистичний розподіл вибірки можна зобразити графічно у вигляді ламаної лінії, відрізки якої сполучають координати точок (xi; ni), або (xi; Wi). У першому випадку ламану лінію називають полігоном частот, у другому — полігоном відносних частот.
Гістограма частот та відносних частот. Гістограма частот являє собою фігуру, яка складається з прямокутників, кожний з яких має основу h і висотy Гістограма відносних частот є фігурою, що складається з прямокутників, кожний з яких має основу завдовжки h і висоту, що дорівнює
Площа гістограми частот Площа гістограми відносних частот Статистичні оцінки параметрів розподілу і загальні вимоги до них. Визначення статистичної оцінки Інформація, яку дістали на основі обробки вибірки про ознаку генеральної сукупності, завжди міститиме певні похибки, оскільки вибірка становить лише незначну частину від неї (n < N), тобто обсяг вибірки значно менший від обсягу генеральної сукупності.Тому слід організувати вибірку так, щоб ця інформація була найбільш повною (вибірка має бути репрезентативною) і забезпечувала з найбільшим ступенем довіри про параметри генеральної сукупності або закон розподілу її ознаки. Параметри генеральної сукупності M(xi)=Xг, Dг, δг, Mo, rxy є величинами сталими, але їх числове значення невідоме. Ці параметри оцінюються параметрами вибірки: Тут через θ позначено оцінювальний параметр генеральної сукупності, а через Числові характеристики статистичного розподілу вибірки. Початкові та центральні вибіркові моменти Величину, яка визначається формулою
називають вибірковою середньою величиною дискретного статистичного розподілу вибірки. Тут xi — варіанта варіаційного ряду вибірки; ni — частота цієї варіанти; n — обсяг вибірки ( Якщо всі варіанти з’являються у вибірці лише по одному разу, тобто ni =1, то
2) дисперсія. Для вимірювання розсіювання варіант вибірки відносно Дисперсія вибірки — це середнє арифметичне квадратів відхилень варіант відносно
або
3) середнє квадратичне відхилення вибірки sB. При обчисленні D B відхилення підноситься до квадрата, а отже, змінюється одиниця виміру ознаки Х, тому на основі дисперсії вводиться середнє квадратичне відхилення
яке вимірює розсіювання варіант вибірки відносно 4) мода (Mo*). Модою дискретного статистичного розподілу вибірки називають варіанту, що має найбільшу частоту появи. Мод може бути кілька. Коли дискретний статистичний розподіл має одну моду, то він називається одномодальним, коли має дві моди — двомодальним і т. д.; 5) медіана (Me*). Медіаною дискретного статистичного розподілу вибірки називають варіанту, яка поділяє варіаційний ряд на дві частини, рівні за кількістю варіант; Умовні варіанти. Умовні емпіричні моменти. Коефіцієнт асиметрії та ексцесу Умовним статистичним розподілом ознаки У при фіксованому значені ознаки Х=хі називають перелік варіант ознаки У та відповідних їм частот, узятих при фіксованому значенні Х. У/Х=хj
1) Коеф асиметрії As*.
2) Ексцес
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 650; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.201.240 (0.008 с.) |



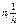 .
. .
.


 .
.
 які дістають при обробці вибірки. Вони є величинами непередбачуваними, тобто випадковими.
які дістають при обробці вибірки. Вони є величинами непередбачуваними, тобто випадковими. — його статистичну оцінку, яку називають ще статистикою. При цьому θ = const, а
— його статистичну оцінку, яку називають ще статистикою. При цьому θ = const, а  — випадкова величина, що має певний закон розподілу ймовірностей. Зауважимо, що до реалізації вибірки кожну її варіанту розглядають як випадкову величину, що має закон розподілу ймовірностей ознаки генеральної сукупності з відповідними числовими характеристиками:M(xi)=Xг=M(x), D(xi)=Dг, δ(xi)=δг
— випадкова величина, що має певний закон розподілу ймовірностей. Зауважимо, що до реалізації вибірки кожну її варіанту розглядають як випадкову величину, що має закон розподілу ймовірностей ознаки генеральної сукупності з відповідними числовими характеристиками:M(xi)=Xг=M(x), D(xi)=Dг, δ(xi)=δг
 ).
).
 вибирається дисперсія.
вибирається дисперсія. , яке обчислюється за формулою
, яке обчислюється за формулою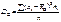


 , але в тих самих одиницях, в яких вимірюється ознака Х;
, але в тих самих одиницях, в яких вимірюється ознака Х;
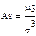 Якщо варіанти розподілені симетрично, то As* =0. При As*<0 варіанти статистичного розподілу вибірки хі<x Таку симетрію:= від’ємною. При As*>0 хі>x, то таку асиметрію:= додатною.
Якщо варіанти розподілені симетрично, то As* =0. При As*<0 варіанти статистичного розподілу вибірки хі<x Таку симетрію:= від’ємною. При As*>0 хі>x, то таку асиметрію:= додатною. Es*, як правило вик при досліджені неперервних ознак генер. сукупностей, оскільки він оцінює крутизну зміни нвв порівняно з нормальним законом. Для нормального Es*=0
Es*, як правило вик при досліджені неперервних ознак генер. сукупностей, оскільки він оцінює крутизну зміни нвв порівняно з нормальним законом. Для нормального Es*=0


