
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точкові статистичні оцінки параметрів розподілу генеральної сукупностіСодержание книги
Поиск на нашем сайте Точкова статистична оцінка називається ґрунтовною, якщо у разі необмеженого збільшення обсягу вибірки що покриває оцінюваний параметр θ генеральної сукупності з заданою надійністю g, називають довірчим. Інтервальні оцінки параметрів розподілу. Надійна ймовірність і надійний інтеграл Статистична оцінка Надійний інтервал для MX і DX нормального розподілу. Визначення мінімального обсягу вибірки. У разі коли озн. Х маж нормальний закон розподілу, для побудови довірчого інтервалу із заданою надійністю для D, σ застосовується вв
Підставимо
Отже надійний інтервал:
Тоді для σ буде:
Значення х1, х2 з таблиць за рівностями: Р(х^2>x1^2)=1-a/2 P(x^2>x2^2)=a/2, a=1-γ
Поняття статистичної гіпотези і статистичного критерію. Помилки першого і другого роду Нульова та альтернативна статистичні гіпотези Гіпотезу, що підлягає перевірці, називають основною. Оскільки ця гіпотеза припускає відсутність систематичних розбіжностей (нульові розбіжності) між невідомим параметром генеральної сукупності і величиною, що одержана внаслідок обробки вибірки, то її називають нульовою гіпотезою і позначають Н 0. Зміст нульової гіпотези записується так: 53) Статистичний критерій Для перевірки правильності висунутої статистичної гіпотези вибирають так званий статистичний критерій, керуючись яким відхиляють або не відхиляють нульову гіпотезу. Статистичний критерій, котрий умовно позначають через K, є випадковою величиною, закон розподілу ймовірностей якої нам заздалегідь відомий. Так, наприклад, для перевірки правильності Загальна схема перевірки статистичних гіпотез. Перевірка достовірності гіпотез про частку ознаки генеральної сукупності, про рівність частот ознаки двох вибірок, про значення генеральної середньої, про рівність двох генеральних середніх і дисперсій Перевірка правельності нульової гіпотези про нормальний закон розподілу ознаки генеральної сукупності Для перевірки правильності Н 0 задається так званий рівень значущості a. a — це мала ймовірність, якою наперед задаються. Вона може набувати значення a = 0,005; 0,01; 0,001. В основу перевірки Н 0 покладено принцип 1. Сформулювати Н 0 й одночасно альтернативну гіпотезу Н a. 2. Вибрати статистичний критерій, який відповідав би сформульованій нульовій гіпотезі. 3. Залежно від змісту нульової та альтернативної гіпотез будується правобічна, лівобічна або двобічна критична область, а саме: нехай
4. Для побудови критичної області (лівобічної, правобічної чи двобічної) необхідно знайти критичні точки. За вибраним статистичним критерієм та рівнем значущості a знаходяться критичні точки. 5. За результатами вибірки обчислюється спостережуване значення критерію 6. Відхиляють чи приймають нульову гіпотезу на підставі таких міркувань: у разі, коли для двобічної критичної області або
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 805; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

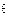 наближається до оцінювального параметра θ, а саме:
наближається до оцінювального параметра θ, а саме:  Точкові статистичні оцінки
Точкові статистичні оцінки  часто призводить до істотних похибок, особливо коли обсяг вибірки малий. У цьому разі застосовують інтервальні статистичні оцінки. Статистична оцінка, що визначається двома числами, кінцями інтервалів, називається інтервальною. Різниця між статистичною оцінкою
часто призводить до істотних похибок, особливо коли обсяг вибірки малий. У цьому разі застосовують інтервальні статистичні оцінки. Статистична оцінка, що визначається двома числами, кінцями інтервалів, називається інтервальною. Різниця між статистичною оцінкою  та її оцінювальним параметром θ, взята за абсолютним значенням, називається точністю оцінки, а саме:
та її оцінювальним параметром θ, взята за абсолютним значенням, називається точністю оцінки, а саме: 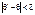 (04) де δ є точністю оцінки. Оскільки
(04) де δ є точністю оцінки. Оскільки  є випадковою величиною, то і δ буде випадковою, тому нерівність (04) справджуватиметься з певною ймовірністю. Імовірність, з якою береться нерівність (04), тобто
є випадковою величиною, то і δ буде випадковою, тому нерівність (04) справджуватиметься з певною ймовірністю. Імовірність, з якою береться нерівність (04), тобто  , (05) називають надійністю. Рівність (05) можна записати так:
, (05) називають надійністю. Рівність (05) можна записати так:  . Інтервал
. Інтервал  ,
, яка визначається одним числом, точкою, називається точковою. Беручи до уваги, що
яка визначається одним числом, точкою, називається точковою. Беручи до уваги, що  є випадковою величиною, точкова статистична оцінка може бути зміщеною і незміщеною: коли математичне сподівання цієї оцінки точно дорівнює оцінювальному параметру θ, а саме:
є випадковою величиною, точкова статистична оцінка може бути зміщеною і незміщеною: коли математичне сподівання цієї оцінки точно дорівнює оцінювальному параметру θ, а саме:  (1) то
(1) то  точкова статистична оцінка
точкова статистична оцінка  називається зміщеною відносно параметра генеральної сукупності θ. Різниця
називається зміщеною відносно параметра генеральної сукупності θ. Різниця  (3) називається зміщенням статистичної оцінки
(3) називається зміщенням статистичної оцінки  Оцінювальний параметр може мати кілька точкових незміщених статистичних оцінок Точкова статистична оцінка називається ефективною, коли при заданому обсязі вибірки вона має мінімальну дисперсію. Отже, оцінка
Оцінювальний параметр може мати кілька точкових незміщених статистичних оцінок Точкова статистична оцінка називається ефективною, коли при заданому обсязі вибірки вона має мінімальну дисперсію. Отже, оцінка 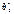 буде незміщеною й ефективною.
буде незміщеною й ефективною.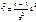 , що має розподіл х2 із К=n-1 ступенями свободи оскільки випадкові події А(х12 < x2 < x22) В(1/х12 < 1/x2 < 1/x22) є рівномірними, маємо: Р(х12 < x2 < x22) = Р(1/х12 < 1/x2 < 1/x22)
, що має розподіл х2 із К=n-1 ступенями свободи оскільки випадкові події А(х12 < x2 < x22) В(1/х12 < 1/x2 < 1/x22) є рівномірними, маємо: Р(х12 < x2 < x22) = Р(1/х12 < 1/x2 < 1/x22) , маємо:
, маємо:



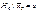 ;
;  ;
;  . Кожній нульовій гіпотезі можна протиставити кілька альтернативних (конкуруючих) гіпотез, які позначають символом Н a, що заперечують твердження нульової. Так, наприклад, нульова гіпотеза стверджує:
. Кожній нульовій гіпотезі можна протиставити кілька альтернативних (конкуруючих) гіпотез, які позначають символом Н a, що заперечують твердження нульової. Так, наприклад, нульова гіпотеза стверджує: 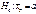 , а альтернативна гіпотеза —
, а альтернативна гіпотеза — 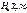 , тобто заперечує твердження нульової.
, тобто заперечує твердження нульової.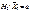 як статистичний критерій K можна взяти випадкову величину, яку позначають через K = Z, що дорівнює
як статистичний критерій K можна взяти випадкову величину, яку позначають через K = Z, що дорівнює  і яка має нормований нормальний закон розподілу ймовірностей. При великих обсягах вибірки (n > 30) закони розподілу статистичних критеріїв наближатимуться до нормального. Спостережуване значення критерію, який позначають через K *, обчислюють за результатом вибірки.
і яка має нормований нормальний закон розподілу ймовірностей. При великих обсягах вибірки (n > 30) закони розподілу статистичних критеріїв наближатимуться до нормального. Спостережуване значення критерію, який позначають через K *, обчислюють за результатом вибірки. , тобто ймовірність того, що статистичний критерій потрапляє в критичну область
, тобто ймовірність того, що статистичний критерій потрапляє в критичну область  , дорівнює малій імовірності a. Якщо ж виявиться, що
, дорівнює малій імовірності a. Якщо ж виявиться, що 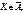 а ця подія малоймовірна і все ж відбулася, то немає підстав приймати нульову гіпотезу. Пропонується такий алгоритм перевірки правильності Н 0:
а ця подія малоймовірна і все ж відбулася, то немає підстав приймати нульову гіпотезу. Пропонується такий алгоритм перевірки правильності Н 0: , тоді, якщо
, тоді, якщо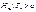 , то вибирається правобічна критична область, якщо
, то вибирається правобічна критична область, якщо , то вибирається лівобічна критична область і коли
, то вибирається лівобічна критична область і коли , то вибирається двобічна критична область.
, то вибирається двобічна критична область. .
.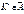 , а це є малоймовірною випадковою подією,
, а це є малоймовірною випадковою подією,  і, незважаючи на це, вона відбулася, то в цьому разі Н 0 відхиляється: для лівобічної критичної області
і, незважаючи на це, вона відбулася, то в цьому разі Н 0 відхиляється: для лівобічної критичної області  ; для правобічної критичної області
; для правобічної критичної області 
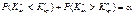
 , ураховуючи ту обставину, що критичні точки
, ураховуючи ту обставину, що критичні точки  і
і  симетрично розташовані відносно нуля.
симетрично розташовані відносно нуля.


