
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Асимптотичні властивості МНК-оцінок.Содержание книги
Поиск на нашем сайте
В багатьох випадках скінченовимірні властивості оцінок найменших квадратів, описані вище, можуть не зберігатись. Так, якщо збурення не є нормально розподіленими, то і розподіл МНК-оцінки вже не буде нормальним. Якщо порушується умова, що всі При послаблені деяких з класичних припущень або при переході до інших моделей скінченновимірні властивості оцінок як правило, невідомі. В таких випадках для характеризації інший підхід, який грунтується на асимптотичній теорії. Асимптотична теорія відповідає на питання, що трапиться, якщо гіпотетично розмір виборки стане нескінченно великим. Асимптотичні властивості використовуються для апроксимації скінченновимірних властивостей. Консистентність. Послідовність оцінок
На відміну від ситуації незалежної виборки тут нам знадобляться додаткові умови стосовно матриці значень незалежних змінних Стосовно збурень достатньо двох припущень
Зауважимо, що умови консистеності не потребують припущень про рівність дисперсій і некорельованість збурень. При виконанні уведених умов
Умова
оінки параметрів будуть зміщеними, але будуть консистентними, якщо Кажучи, не зовсім строго, консистентність означає, що при зростанні розділу виборки ймовірність того, що оцінки будуть набагато відрізнятись від параметра прямує до нуля. В багатьох випадках неможливо довести незміщеність оцінки, або, взагалі, незміщену оцінку знайти неможливо (наприклад, для нелінійних моделей, або моделей з лаговими значеннями залежної змінної серед регресорів, як в попередньому прикладі). В таких ситуаціях мінімальною вимогою до оцінок є консистентність. Зручною властивістю є наступна. Якщо Асимптотична нормальність. Властивість асимптотичної нормальності дозволяє використовувати стандартні критерії перевірки гіпотез без припущення про нормальність збурень, оскількі відповідні статистики, приблизно, матимуть потрібні розподіли. Припустимо, що крім припущень, уведених у попередньому параграфі виконують припущення про рівність дисперсій і некорельованість збурень. Тоді
що співпадає з точною формулою у випадку класичних нормально розподілених збурень. Моделі в яких порушуються припущення про рівність дисперсії і про некорельованість збурень розглядаються, відповідно, у темах “гетероскедастичність” і “автокореляція ”. В цих ситуаціях поруч зі специфічними методами можна використовувати звичайний метод найменших квадратів, але при цьому слід використовувати інші оцінки коваріаційної матриці b. МНК-оцінки зберігають властивість асимптотичної нормальності:
де замість S слід підставити оцінки, які наведено у відповідних параграфах.
1.4. Модель лінійної регресії з гетероскедастичними збуреннями. 1.4.1. Вступ В цьому розділі ми розглянемо регресійні моделі, в яких порушується припущення 2 – про рівність дисперсій збурень. Проаналізуємо залежність особистого споживання від доходу. Згадаємо, що збурення в моделі лінійної регресїї можна вважати відхиленням рівня споживання конкретного домогосподарства від середнього рівня, який відповідає даному розміру доходу. Логiчно очiкувати, що для домогосподарств з більшими доходами спостерiгатиметься бiльший розкид рівнів споживання. Отже, оскільки дисперсія збурень є мірою цого розкиду, то припущення про рівність дисперсій збурень в такій моделі буде нереалістичним. Наведений приклад показує необхідність вивчення нового класу моделей, які узагальнюють класичну модель лінійної регресії – моделей з гетероскедастичними збуреннями. Опис моделi. Нам знадобляться наступні позначення. Літерою u позначимо вектор збурень у вихідній моделі, а літеру e зарезервуємо для позначення збурень, які задовольняють припущенням 1 – 5 з параграфа 1.2.1. Розглянемо модель лінійної регресії
або, якщо ми маємо модель з константою,
в якій вектор збурень u = (u1, u2... u n)T має такi властивостi: 1. 2. Гетероскедастичність збурень: Du i = 3. Незалежність збурень: u і та u j незалежні при 4. Незалежність збурень та регресорів: xij та u і незалежні для всіх i та j. 5. (Додаткове) Збурення u i нормально розподілені для всіх i. Припущення 2 і 3 зручно записувати у матричному вигляді:
1.4.3. Наслiдки гетероскедастичності збурень на оцiнки методу найменших квадратiв 1.Оцiнки МНК будуть незмiщеними, але не будуть ефективними (не матимуть найменшої дисперсiї). 2.Стандартнi оцiнки коварiацiйної матрицi оцiнки МНК будуть змiщеними, i, як наслiдок, процедури перевiрки гiпотез та iнтервального оцiнювання, основанi на стандартних статистиках, будуть некоректними.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 331; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.118.214 (0.015 с.) |

 некорельовані зі всіма
некорельовані зі всіма 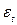 , математичне сподівання b не дорівнюватиме
, математичне сподівання b не дорівнюватиме 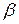 . Більш того, модель лінійної регресії, збурення в якій задовольняє всі класичні умови є однєю з небагатьох в економетриці, коли відомий точний скінченновимірний розподіл оцінок параметрів.
. Більш того, модель лінійної регресії, збурення в якій задовольняє всі класичні умови є однєю з небагатьох в економетриці, коли відомий точний скінченновимірний розподіл оцінок параметрів. параметра
параметра  , де
, де  - розмір виборки, називається консистентною якщо
- розмір виборки, називається консистентною якщо  збігаються за ймовірністю до справжнього значення параметра:
збігаються за ймовірністю до справжнього значення параметра: , тобто
, тобто

 . Припустимо, що
. Припустимо, що  збігається до несингулярної матриці
збігається до несингулярної матриці  . Точці умови, що забезпечують збіжність
. Точці умови, що забезпечують збіжність 
 .
. є значно слабшою у порівнянні з умовою про некорельованість всіх
є значно слабшою у порівнянні з умовою про некорельованість всіх  а не тільки з
а не тільки з  , яка необхідна для забезпечення незміщенності. Так, наприклад, в моделі
, яка необхідна для забезпечення незміщенності. Так, наприклад, в моделі

 і
і  є неперервною функцією,то
є неперервною функцією,то 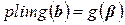 . Зауважимо також, що для консистентності
. Зауважимо також, що для консистентності  як оцінки
як оцінки  до уведених умов слід додати умову про рівність дисперсій збурень.
до уведених умов слід додати умову про рівність дисперсій збурень. збігається за розподілом до
збігається за розподілом до  . Оскільки невідома матриця
. Оскільки невідома матриця  консистентно оцінюється за допомогою
консистентно оцінюється за допомогою  , а
, а  ,
,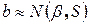 ,
, , (1.73)
, (1.73) , (1.74)
, (1.74)
 ,
,  ,
,  при
при  .
. .
. (1.75)
(1.75)


