
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття часового лагу. Моделі з часовим лагом незалежних змінних.Содержание книги
Поиск на нашем сайте
Моделі, у яких досліджуваний показник у момент часу t визначається не лише поточними, а й попередніми значеннями незалежних змінних, наз дистрибутивно-лаговими. Якщо в економетричній моделі незалежні змінні використовують за кілька попередніх періодів, то такі моделі називають моделями з кінцевим лагом (скінченними моделями). Якщо вплив незалежної змінної не обмежується певним періодом, розглядають нескінченні лагові моделі. Звичайно, нескінченна лагова модель більш загальна, однак практичне застосування такої моделі досить проблематичне через велику кількість факторів, складність внутрішньої структури та обмеженість часових рядів - інформаційної бази моделей. Коефіцієнт а0 при незалежній змінній xt, що відбиває її вплив на залежну змінну в поточний період, називається короткостроковим, або впливовим, мультиплікатором. Для нескінченної моделі лагові коефіцієнти за певних умов також можуть утворити скінченну суму. Якщо кожен із коефіцієнтів розділити на їх суму, отримаємо відповідно нормовані коефіцієнти лага та нормовану структуру лага. Усі нормовані коефіцієнти менші від одиниці, а їх сума дорівнює одиниці. Дистрибутивно-лагові моделі, які ще називають моделями розподіленого лага, задовільно описують економічні процеси лише в стабільних (незмінних) умовах. Необхідність враховувати ще й поточні умови функціонування вимагає застосування узагальнених моделей. Авторегресійні моделі. Моделі, у яких досліджуваний показник у момент часу t визнач-я своїми попередніми значеннями, називаються авторегресійними або динамічними моделями. Оцінюв-я авторегресійних моделей з часовим лагом незалежних змінних. Метод Кочрена-Оркатта є ітеративним методом оцінювання параметрів економетричної моделі, коли мінімізується сума квадратів залишків, яка для моделі Пон-я тренду, сезон, цикл та випадк компоненти Аналіз часового ряду починається з виділ-я трендового компонента. Його присутність неважко помітити, проаналізувавши графік часового ряду. Наявність тренду в екон часових рядах можна пояснити демографічними змінами, технологічними змінами, змінами в структурі вир-ва, попиту. Дія таких факторів є постійною, тому дослідники мають змогу описувати такі зміни за доп-ою кривих, які можна задати в аналітичному вигляді. Сезонний компонент показує коливання навколо трендового компонента. Його наявність пояснюється сезонним характером виробництва, споживання. Циклічний компонент займає проміжне місце між трендом та сезонним компонентом, гладка зміна, залежна від часу, але яка не включається ні до тренду, ні до сезонного компонента. Випадковий компонент є те, що залишилось від часового ряду після виключення тренду, циклічного та сезонного компонентів. Частина таких ефектів може бути віднесена до непередбачених природних катаклізмів (землетруси, пожежі, тощо), частина – до випадкових дій людей.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 339; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.105.110 (0.006 с.) |


 визнач-я так:
визнач-я так: 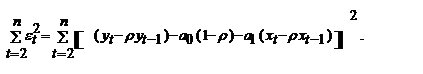 Розглянемо алгоритм Крок 1. Приймається гіпотеза
Розглянемо алгоритм Крок 1. Приймається гіпотеза  і мінімізується на основі 1МНК сума квадратів:
і мінімізується на основі 1МНК сума квадратів:  . Отже, так само й далі обчислюються параметри для моделі Крок 2. Знаходяться залишки і перевіряється нульова гіпотеза відносно автокореляції залишків. Якщо гіпотеза відхиляється, то переходять до кроку 3. Крок 3. На даному кроці мінімізується сума квадратів відхилень:
. Отже, так само й далі обчислюються параметри для моделі Крок 2. Знаходяться залишки і перевіряється нульова гіпотеза відносно автокореляції залишків. Якщо гіпотеза відхиляється, то переходять до кроку 3. Крок 3. На даному кроці мінімізується сума квадратів відхилень:  де
де  і
і  - оцінки параметрів, знайдені на першому кроці 1МНК. У результаті параметр
- оцінки параметрів, знайдені на першому кроці 1МНК. У результаті параметр  визначається як коефіцієнт регресії залишків, знайдених 1МНК, на їх лагові змінні, які стосуються минулого періоду. Крок 4. Використовуючи значення оцінки параметра
визначається як коефіцієнт регресії залишків, знайдених 1МНК, на їх лагові змінні, які стосуються минулого періоду. Крок 4. Використовуючи значення оцінки параметра  , визначають оцінки параметрів
, визначають оцінки параметрів  і
і  на основі 1МНК, який застосовується до перетворених даних
на основі 1МНК, який застосовується до перетворених даних 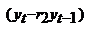 і
і  . Крок 5. Визначаються залишки і перевіряються на наявність автокореляції. Якщо гіпотеза про наявність автокореляції відхиляється, то ітеративний процес припиняється. У противному разі переходимо до кроку 3, де використовуються знайдені оцінки параметрів
. Крок 5. Визначаються залишки і перевіряються на наявність автокореляції. Якщо гіпотеза про наявність автокореляції відхиляється, то ітеративний процес припиняється. У противному разі переходимо до кроку 3, де використовуються знайдені оцінки параметрів  і
і  .
.


