
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття економ-ої моделі, її складові частиниСодержание книги Поиск на нашем сайте
Поняття економ-ої моделі, її складові частини Економ-а модель - функція чи система ф-ій, що описує кореляційно-регресійний зв’язок між екон показниками, причому залежно від причинних зв’язків між ними один чи кілька із цих показників розгляд-я як залежні змінні, а інші - як незалежні. У заг-у випадку рівняння в економ-ій моделі має вигляд: Y=f(x1, x2,…,Xm,u), де У- резул-т, або залежна змінна, змінюв-я якої описує дане рівн-я; х1, х2,..., хm - фактори, або незалежні змінні, що визнач-ь поведінку У, u - стохастична складова. Економ-а модель склад-я: 1)Набір рівнянь поведінки, які вивод-я з екон-ї моделі. Ці рівняння включ-ь деякі змінні, знач-я яких спостеріг-я, а також «збурення», які відтвор-ь ефект від змінних, не включ-их до моделі у явному вигляді, та ефект від непередбачуваних подій. 2)Опис імовірнісного розподілу «збурень» (помилок). Роль, місце економ моделей в управл ек сист-и Сучасні методи управл-я екон системами та процесами баз-я на широкому викор-і математ-их методів та ЕОМ. Коли в екон науці постали задачі, які не вдається розв’язати за доп-ою традиційних екон методів, матем-ка посіла в цій науці одне з осн-их місць. Сформув-я напрямок теоретично-практичних досліджень - екон-ко-матем-не моделюв-я, що є вираж-ям процесу математизації наукового екон знання. Економ-ні моделі кількісно описують зв’язок між вхідними показниками екон системи (X) та результативним показником (Y). У аг-му вигляді економ-ну модель можна записати так: Y = f(X,u), де X - вхідні екон показники; u - випадкова, або стохастична, складова. Прич, що спон появу випад склад-ої e регрес мод Стохастичну складову ε економ-ої моделі наз помилкою (залишком, збуренням, відхил-ям). Причини виникн-я: 1)Регресійна модель являє собою складне переплет-я різних факторів, багато з яких фізично не можна врахувати в моделі. 2)Неправильно вибрана форма функц-ої залежності між змінними в моделі через недостатнє дослідж-я процесу, який підлягає моделюв-ю, або неправильно вибрані пояснювальні змінні. 3)Агрегув-я змінних. Залежн-ь між факторами являють собою залежн-і між цілими комплексами подібних величин. 4)Помилки вимірюв-я, які можуть бути допущ-і під час аналізу й обробки статист-их даних. 5)Обмеж-ь статист-их даних проявл-я в тому, що більшості моделі виражаються переважно неперервними функціями, але при цьому використовується набір даних, що має дискретну структуру. 6)Непередбаченість людського фактора, може бути одним із головних проявів відхилень незал-ої змінної в модельованих знач-ях.
Етапи побудови економетричної моделі Етапи побудови економ-ої моделі: 1)Знайомство з екон теорією, висун-я гіпотези взаємозв’язку. Чітка постановка задачі. 2)Специф-я моделі, тобто сформул-я теоретичних уявл-ь і прийнят-я гіпотези у вигляді мате мат-их рівнянь, які встановл-ь зв’язки між осн-и визначальними змінними за припущ-я, що всі інші змінні є випадковими. 3)Формув-я масивів вихідної інформації згідно з метою та завдан-и дослідж-я. 4)Оцінка параметрів економ-ої моделі МНК, що дає змогу про аналіз-и залишки і визнач чи не суперечить специфікація моделі передумовам “класичної” моделі лін-ої регресії. 5)Якщо деякі передумови моделі не викон-я, то для продовж-я аналізу треба замін-и специфікацію або застосов-и інші методи оцінюв-я параметрів. 6)Провед-я аналізу вірогідності моделі та визнач-я прогнозу за побудов-ою моделлю. Специфікація економетричних моделей Специфікація моделі - аналіт-а форма залежності між екон-и показниками. Незалежні змінні х1,х2,…,хm, що задані заздалегідь чи за межами моделі, наз екзоген-и змінними (регресорами). Залежна змінна У, що визнач-я як розв’язок рівняння, наз ендогенною змінною (регресантом). Функція f у кожному конкретному випадку окрім змінних х1,х2,…,хm і u містить ще щонайменше деякі коефіцієнти, що поєднують змінні у певних співвідношеннях і визначають структуру рівняння. Ці коефіцієнти наз параметрами моделі. Помилки специфікації моделей регресії Помилки специфік-ії моделі можуть бути: 1)ігнорув-я істотності пояснюючої змінної при побудові економ-ої моделі, що призводить до зміщ-я оцінок параметрів, тому застосув-я способів перевірки їх значущості може сприт-и до хибних висновків щодо значень параметрів генерал-ої сукупності; 2)введ-я до моделі незалежної змінної, яка не стос-я вимірюваного зв’язку, яка неістотно впливає на залежну змінну, що призвод-ь до того, що оцінки параметрів моделі будуть незмін-и; 3)викор-я не відповідних матем-их форм залежності (припуск-я, що залежна змінна є лінійною ф-ією від деякої пояснювальної змінної, хоча тут краще застос-и квадратичну, кубічну.
Коеф. детерм-ї (КД) та корел-ї (КК) для моделі парної регресії. Перевірка суттєвості КД за допом. F-крит. КД і КК - кіл-ні хар-ки дисперс-го аналізу, за якими можна зробити висновок - наскільки побудована економетр. (Е) модель узгоджується з емпіричною інформацією, на підставі якої її побудовано, тобто чи достовірна Е модель. КД показує на скільки % варіація залежної змінної визначається варіац. незалеж. змінних. R2=1-(Σli2/Σ(yi-yсер)2). КК характер. тісноту зв’язку між залеж. і пояснювальними змінними. R=√R2. Значення КД і КК належать множині: [0;1]. Чим ближчі ці значення до 1, тим істотніший зв’язок між змінними Е моделі і адекватніша ця модель даним спостережень. Гіпотеза про істотність зв’язку між зал. і незал. змінними може бути перевірена за допом. F-критерія: 1)знах. Fp=R2*(n-2)/(1-R2). 2)знах. Fкр за табл-ми F-розподілу Фішера при ступенях вільності к1=1; к2=n-2 і обраною надійністю Р. 3)Fp порівнюється з Fкр. Якщо Fp>Fкр, то модель адекватна і R2 суттєво відрізняється від 0 і навпаки при Fp<Fкр.. Перевірка сутт-і оцінок парам-ів на осн-і t-крит-ію Перевірку гіпотези про значущість параметрів економетр. моделі можна виконати згідно з t-критерієм: 1)знах. tp=aj/σ^aj. 2)знах tкр за таблицями t-критерія Стьюдента для обраного рівня значимості α і числа ступенів вільності к=n-m-1. 3) tp порівнюється з tкр. Якщо |tp|>tкр, то Н0 відхиляється і оцінку параметра aj можна вважати значимою і навпаки при |tp|<tкр. Точк. Т та інтервал-й І прогноз на основі моделі парної регресії. Існує 2 види прогнозування: (Т) і (І). Припустимо, що нам відоме значення фактора для (n+1) періоду, тоді можна отримати прогнозне знач. у^n+1 за допом. моделі: у^n+1=а0+а1х1,n+1 - (Т) прогноз значень показника. (І) прогноз можна отримати так: (у^n+1-Dу^n+1; у^n+1+Dу^n+1), де Dу^n+1=tкр*σ^у^n+1; σ^у^n+1=√S2*(1+1/n+((xi-xcep)2/Σ(xi-xcep)2)). Передумови застосув-я МНК для оцінки пар-ів парної лінійної регресії Економетр. модель має вигляд Y=а0+а1*Х+u, де Y —значення залеж. змінної; X —незал. змінна; а0 і а1 —оцінки параметрів моделі; u —залишок. Щоб застосувати МНК, необхідне виконання таких передумов: 1)мат. сподівання залишка = нулю: М(u)=0. 2)дисперсія залишка незалежно від номера спостережень є постійною. МНК оцінюв-я пар-ів множинної лінійної регресії. МНК полягає в знаходженні таких оцінок параметрів а0, а1… аm за яких сума квадратів відхилень Σli2 спостережуваних знач. показника від розрахункових буде найменша. Формула для оцінки параметрів множ. лін. регресії: {A}=[[X]T*[X]]-1*[X]T*{Y}. МНК доцільно застосов-и, коли залишки розпад-і нормально, тобто їх середнє знач-я = 0 і дисперсія стала. Властив-і оцінок параметрів, знайдених за МНК Оцінки параметрів є вибірковими хар-ми, що мають такі властивості: 1) незміщеність Н - мін. вимога, яка ставиться до оцінок параметрів. Якщо оцінка Н, то за багаторазового повторення випадкової вибірки сер. значення похибок =0. 2) ефективність Е. Вибіркові оцінки вектора параметрів А будуть Е тоді, коли їх дисперсії є найм. в класі незміщених оцінок. Величина дисперсії оцінок пар-ів залежить від кіл-ті спостережень, специфікації моделі та ефективного методу оцінювання цих параметрів. 3) обґрунтованість оцінки означає, що чим більші будуються вибірки, тим більша ймовірність того, що похибка оцінки не перевищуватиме достатньо малого значення e. 4) інваріантність оцінки базується на тому, що в разі перетворення параметрів А за допомогою деякої функції g таке саме перетворення, виконане щодо A', дає оцінку g(A') нового параметра. Має велике практичне значення.
Алгоритм Фаррара-Глобера. Найповніше дослідити мультик-ть можна за доп алгоритму Ф-Г. Цей алгоритм має 3 види статистичних критеріїв, за якими перевіряється М-ть усього масиву незалежних змінних (c2); кожної незалежної змінної з усіма іншими (F-критерій); кожної пари незалежних змінних (t-критерій). Алгоритм Ф-Г скл-ся із 7 кроків: 1.Стандартизація (нормалізація) змінних 7.Обчислення t-критеріїв: Алгоритм теста Глейсера. Глейсер запропонував розглядати регресію абсолютних значень залишків |ui|, які відпов-ь регресії найменших квадратів як деяку ф-ію від xj, де xj є тією незалежною змінною, яка відповідає зміні дисперсії s2u. Для цього викор-ся такі види ф-ій: 1.|u|= a0+ a1* xj; 2.|u|= a0+ a1* xj^(-1); 3.|u|= a0+ a1* xj^(1/2) і т.п. Рішення про відсутність гетероск-ті залишків прийм-я на основі статист-ої значущості коеф-ів a0 й a1. Переваги цього тесту визнач-я можливістю розрізняти випадок чистої і змішаної гетероск-ті. Чистій гетер-ті відповід-ь знач-я параметрів a0=0, a1≠0; а змішаній - a0≠0, a1≠0. Залежно від цього треба корист-ь різними матрицями S (M(uu’)=s2uS). Якщо при економетр-му моделюв-і для певних вихідних даних буде виявлено явище гетероск-ті, то оцінку параметрів моделі треба викон-и на основі узагальн-о МНК. Прогноз на основі економетр-ї моделі, в якій оцінка параметрів виконана узагал-им МНК, можна отримати на основі такого співвіднош-я: Ŷпр=X0 A+W’V-1U, де u - вектор залишків, який відповідає оцінці параметрів моделі на основі МНК; W’ - транспонований вектор коваріацій поточних і прогнозних значень залишків; V-1=S-1, а V=s2uS. Критерій фон Неймана.
Цикл та нециклічний коефіцієнт автокореляції(А) Нецикл. коеф виражає ступінь взаємозв’язку залишків кожного наступного значення з попереднім.
Він обчислюється за формулою:
Авторегресійні моделі. Моделі, у яких досліджуваний показник у момент часу t визнач-я своїми попередніми значеннями, називаються авторегресійними або динамічними моделями. Криві зростання. Якщо існує певна закономірність в динаміці деякого економічного явища або процесу, то тенденція цієї зміни може бути встановлена добором потрібної функції y(t)=f(t). Найчастіше в ек-ці викор-ся поліном-ні, експонент-і та S-подібні криві зрост-я. Параметри многочленів поліному мають конкретну інтерпретацію (а1-швидк. зрост-я, а2-прискор. зрост. і т. д.) Експонен-а ф-ція Yt=AB^t описує процесс зі сталим темпом зростання і сталим темпом приросту. Процеси, що характер-ся насиченням, описуються модифікованою експонентою Yt=K+AB^t. У маркетингових дослідженнях, відбиваючи основну тенденцію, використовують функцію Гомперця Yt=KA^b(^t). Методи вибору форми тренду. Візуальний - вибір форми тренду на основі графічного зображення динамічного ряду. На результат впливає масштаб графічного зображення. 2-ий спосіб - полягає у викор-і методу послідовних різниць, згідно з яким обчислюється 1-ий, 2-ий та вищий порядки різниць рівнів часового ряду. Обчислення проводиться доти, доки різниці не будуть майже однаковими. Порядок рівності різниці беруть за ступінь многочленна для вирівнювання основної тенденції динаміки. 3-ій спосіб - за критерій вибору форми тренду беруть суму квадратів відхилень значень рівнів від розрах-их. Із множини функцій вибирають таку, якій відповідає мінімальне знач-я цього критерію. 4-ий спосіб - метод характер-ик приростів полягає у тому, що вибір форми кривої відбув-я за попередньою статист-ою обробкою динамічного ряду(ковзна середня, середні прирости згладженого ряду, похідні характеристики приростів). Експоненційне згладжування Метод експоненціального згладжування. У процедурі відшукання загладжуваного рівня застосовується значення тільки попередніх рівнів ряду, взятих з певною вагою, яка зменшується при віддалені від кінця ряду. Вага рівнів знижується експоненціально, залежно від параметра згладжування α(0<α<1). Експоненційне згладжування розраховуэться за такою формулою: St=α*yt+(1- α)*St-1 де α-параметр згладжування. 74. Аналітичні методи згладжування часового ряду. Метод простої сковзної середньої. Для часового ряду y1,y2,y3… yn визнач. інтервал згладж. m(m<n). Для перших m рівнів часового ряду обчислюється їх сер. арифм. Це буде згладжуване значення рівнів ряду, яке відповідає середині інтервалу згладжув-я. Далі інтервал зсувається на один рівень праворуч, повторюється обчислення сер. арифм. Для обчисл. Згладжених рівнів ряду ýt застосовуэмо формулу:
Алгоритм непрямого МНК НМНК дає обґрунтовану оцінку параметрів структ. форми моделі, але вона буде мати зміщення в бік зниження її рівня. Тому цей метод застосовується тільки за точної ідентифікованості рівнянь структурної форми.Алгоритм непрямого методу найменших квадратів:Крок 1. Перевіряється умова ідентифікованості для кожного рівняння структурної форми моделі. Якщо кожне рівняння точно ідентифіковане, то переходимо до кроку 2.Крок 2. Кожне рівняння структурної форми розв'язується відносно однієї з k ендогенних змінних моделі, у результаті приходимо до зведеної форми моделі.Крок 3. Застосовуючи 1МНК, визначається оцінка параметрів окремо для кожного рівняння зведеної форми.Крок 4. Розраховується оцінка параметрів рівнянь структурної форми за допомогою співвідношення AR = -В, де А і В - параметри структурних рівнянь, a R - матриця оцінок параметрів зведеної форми. Прогноз ендогенних змінних. Під час побудови економетричних моделей, як правило, ставиться дві основні цілі. Одна ціль полягає в оцінці параметрів структурних рівнянь, а також рівнянь зведеної форми. Друга ціль — дістати за допомогою моделі умовний прогноз залежних змінних за певних припущень відносно майбутніх значень пояснювальних змінних.Якщо необхідно здобути оцінку структурних коефіцієнтів, то, як було сказано вище, треба скористатись обґрунтованим оператором оцінювання. Якщо досліджувача задовольняють коефіцієнти рівнянь зведеної форми, то їх незміщеність і обґрунтованість може бути досягнута під час застосування 1МНК до кожного рівняння, або узагальненого методу найменших квадратів, що базується на процедурі Зельнера, яка дає змогу оцінити декілька зовні не пов'язаних одне з одним рівнянь. Але ні 1МНК, ні метод Зельнера не накладають будь-яких обмежень на параметри зведеної форми, тоді як такі обмеження існують і вони містяться в системі рівнянь, що зв'язує параметри структурної і зведеної форми, тобто матриці R=-A-1-B. Клейн допускає, що коли специфікацію моделі у структурній формі вибрано правильно, то більш ефективно розрахувати спочатку коефіцієнти матриць А і В, а потім оцінити параметри матриці R, тобто він пропонує знаходити оцінку матриці R так – R^=-A^-1B^: Розглянемо прогноз ендогенних змінних при заданих значеннях екзогенних змінних. Точковий прогноз одержати досить просто, підставивши значення екзогенних змінних в приведену форму рівнянь. Тому, якщо позначити через Xf вектор прогнозних екзогенних змінних, то точковий прогноз залежних ендогенних змінних буде визначатись так: Yf=
Поняття економ-ої моделі, її складові частини Економ-а модель - функція чи система ф-ій, що описує кореляційно-регресійний зв’язок між екон показниками, причому залежно від причинних зв’язків між ними один чи кілька із цих показників розгляд-я як залежні змінні, а інші - як незалежні. У заг-у випадку рівняння в економ-ій моделі має вигляд: Y=f(x1, x2,…,Xm,u), де У- резул-т, або залежна змінна, змінюв-я якої описує дане рівн-я; х1, х2,..., хm - фактори, або незалежні змінні, що визнач-ь поведінку У, u - стохастична складова. Економ-а модель склад-я: 1)Набір рівнянь поведінки, які вивод-я з екон-ї моделі. Ці рівняння включ-ь деякі змінні, знач-я яких спостеріг-я, а також «збурення», які відтвор-ь ефект від змінних, не включ-их до моделі у явному вигляді, та ефект від непередбачуваних подій. 2)Опис імовірнісного розподілу «збурень» (помилок).
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.198.181 (0.013 с.) |

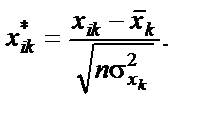 2.Знаходження кореляційної матриці. 3.Визначення критерію c2: c2 = -(n-1-1/6*(2m+5))ln|r|. 4.Визначення оберненої матриці. 5.Обчислення F-критеріїв Fk=(ckk -1)*((n-m)/(m-1)). 6.Знаходження частинних коефіцієнтів кореляції:
2.Знаходження кореляційної матриці. 3.Визначення критерію c2: c2 = -(n-1-1/6*(2m+5))ln|r|. 4.Визначення оберненої матриці. 5.Обчислення F-критеріїв Fk=(ckk -1)*((n-m)/(m-1)). 6.Знаходження частинних коефіцієнтів кореляції: 

 , де
, де  .У даній матриці залежно від висунутої гіпотези: λi=1/ xij; або λi=1/xij^2; або λi={|ȗi|}.
.У даній матриці залежно від висунутої гіпотези: λi=1/ xij; або λi=1/xij^2; або λi={|ȗi|}. (DW – критерій Дарбіна-Уотсона) Фактичне знач-я критерію фон Неймана порівнюється з табличними для вибраного рівня значущості і заданої кількості спостережень. Якщо
(DW – критерій Дарбіна-Уотсона) Фактичне знач-я критерію фон Неймана порівнюється з табличними для вибраного рівня значущості і заданої кількості спостережень. Якщо  , то існує додатна автокореляція, у протилежному випадку - вона відсутня.
, то існує додатна автокореляція, у протилежному випадку - вона відсутня. Коефіцієнт
Коефіцієнт  може набувати (–1;+1). Від’ємні зн його свідчать про від’ємну А, додатні — про додатну. Зн-ня, що містяться в деякій критичній області біля 0, свідчать про відсутність А, тобто стверджують нульову гіпотезу про відсутність А залишків. Циклічний коеф виражає ступінь взаємозв’язку рядів. Обчисл-я за формулою:
може набувати (–1;+1). Від’ємні зн його свідчать про від’ємну А, додатні — про додатну. Зн-ня, що містяться в деякій критичній області біля 0, свідчать про відсутність А, тобто стверджують нульову гіпотезу про відсутність А залишків. Циклічний коеф виражає ступінь взаємозв’язку рядів. Обчисл-я за формулою:  Для досить довгих рядів вплив циклічних членів на величину коеф
Для досить довгих рядів вплив циклічних членів на величину коеф  незначний, тому можна вважати, що ймовірнісний розподіл
незначний, тому можна вважати, що ймовірнісний розподіл  наближається до розподілу
наближається до розподілу  . де i - порядковий номер ряду, p=(m-1)/2. Застосований лише для рядів, що мають лінійну тенденцію. Метод експонен-го згладжув-я. У процедурі відшук-я загладж-о рівня застосов-я знач-я тільки попередніх рівнів ряду, взятих з певною вагою, яка зменш-я при віддалені від кінця ряду. Вага рівнів зниж-я експонент-о, залежно від параметра згладжув-я α(0< α<1). Експоненційне згладжув-я розрахов-я за такою формулою: St=α*yt+(1- α)*St-1. де α-параметр згладжування.
. де i - порядковий номер ряду, p=(m-1)/2. Застосований лише для рядів, що мають лінійну тенденцію. Метод експонен-го згладжув-я. У процедурі відшук-я загладж-о рівня застосов-я знач-я тільки попередніх рівнів ряду, взятих з певною вагою, яка зменш-я при віддалені від кінця ряду. Вага рівнів зниж-я експонент-о, залежно від параметра згладжув-я α(0< α<1). Експоненційне згладжув-я розрахов-я за такою формулою: St=α*yt+(1- α)*St-1. де α-параметр згладжування. *Xf. Визначення довірчих інтервалів для цього прогнозу залежить від методу, за допомогою якого була отримана матриця R. Якбуло сказано раніше, матриця R може бути отримана на основі застосування 1МНК окремо до кожного рівняння зведеної форми,або як
*Xf. Визначення довірчих інтервалів для цього прогнозу залежить від методу, за допомогою якого була отримана матриця R. Якбуло сказано раніше, матриця R може бути отримана на основі застосування 1МНК окремо до кожного рівняння зведеної форми,або як  -1*
-1*  , де структурні коефіцієнти оцінені на основідво- або трикрокового методу найменших квадратів. Якщо специфікацію моделі в структурній формі вибрано правильно, то останній спосіб має перевагу. Якщо ж про точну специфікацію моделі не можна сказати нічого конкретного, то краще оцінювати рівняння зведеної форми за допомогою 1МНК. У такому разі
, де структурні коефіцієнти оцінені на основідво- або трикрокового методу найменших квадратів. Якщо специфікацію моделі в структурній формі вибрано правильно, то останній спосіб має перевагу. Якщо ж про точну специфікацію моделі не можна сказати нічого конкретного, то краще оцінювати рівняння зведеної форми за допомогою 1МНК. У такому разі


