
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оцінювання параметрів простої економетричної моделі методом найменших квадратів.Содержание книги
Поиск на нашем сайте
Звернемося до прикладу простої економетричної моделі, де потрібно кількісно оцінити зв’язок між витратами на споживання та доходами сім’ї (див. підрозд. 2.3). Щоб оцінити параметри моделі (2.16), необхідно сформувати вихідну сукупність спостережень, кожна одиниця якої характеризуватиметься витратами на споживання і доходами сімей. Припустимо, що економетрична модель споживання будується для тієї групи людей, в якій зі збільшенням доходів зростають витрати на споживання, тобто модель має вигляд (2.16).
Зобразимо кожну пару спостережень у системі координат, де величина витрат на споживання відкладається на осі ординат, а доходів — на осі абцис. У результаті дістанемо кореляційне поле точок (рис. 2.2). На підставі гіпотези про лінійність зв’язку між витратами на споживання і доходом сімей (див. рис.2.2), через кореляційне поле точок можна провести безліч прямих ліній, які різняться між собою параметрами Не доцільно знаходити параметри економетричної моделі, мінімізуючи суму лінійних відхилень фактичних витрат на споживання від розрахункових, бо вона може дорівнювати нулю, якщо сума від’ємних і додатних відхилень буде однаковою. Тому мінімізації підлягає сума квадратів відхилень, і величина її залежатиме безпосередньо від розсіювання точок навколо лінії регресії, а саме:
Принцип найменших квадратів відхилень полягає в знаходженні таких
то
Виконавши елементарні перетворення, дістанемо систему нормальних рівнянь
Підставимо в систему (2.19) значення
Оскільки оцінки найменших квадратів такі, що лінія регресії обов’язково проходить через точку середніх значень ( Поділивши перше рівняння системи (2.19) на n, дістанемо:
Віднімемо (2.20) від (2.16):
Нехай
а відхилення фактичних значень від розрахункових будуть такі:
Сума квадратів залишків при цьому
Мінімізація цієї суми за невідомим параметром
Крім того, можна помітити, що Параметр
Співвідношення (2.21) можна було б дістати також, записавши друге рівняння системи (2.19) через відхилення кожної змінної від її середнього арифметичного значення, згадавши при цьому, що сума таких відхилень завжди дорівнює нулю. 5 Передумови застосування методу найменших квадратів. Процедура однокрокового (звичайного) методу найменших квадратів (1МНК) розглянута у п. 2.3. Нагадаємо, що сутність методу полягає у знаходженні таких значень матриці параметрів Амоделі загального вигляду (6.1), при яких сума квадратів залишків и була б мінімальною (2.20). Тоді для фактичних значень залежних змінних Y моделі (6.1) теоретичні (розрахункові) значення змінних Y будуть представлені у вигляді Y - АХ, (6.2) де А - оцінка параметрів теоретичної моделі. Сукупність виразів (6.1) і (6.2) для фактичних і теоретичних значень пояснюваних змінних визначає економетричну модель загального виду: Y — АХ + и; Y - АО.
Мінімізуя суму квадратів залишків и шляхом знаходження першої похідної за складовими А (2.20), можна знайти оцінки А для теоретичної моделі, які в матричному запису будуть мати вигляд А - (ХХ)_1 ХУ, (6.3) де X' - матриця, транспонована до матриці X. Вираз (6.3) є розв’язком так званої системи нормальних рівнянь (ХХ)А - Х'У. (6.4) Оцінювати параметри економетричної моделі за допомогою 1МНК можна за умов: Математичне сподівання залишків, тобто середня величина випадкових значень, дорівнює нулю М(и)=0. (6.5) Якщо ця передумова не виконується, то йдеться про помилки специфікації. Специфікацію моделі називають її аналітичну форму, яка складається з певного виду вибраної функції чи системи функцій для змінних. До помилок специфікації приводять: відсутність у моделі основної пояснювальної (незалежної) змінної, що призводять до зміщення оцінок параметрів і може привести до хибних висновків щодо значень параметрів; введення в модель пояснювальної змінної, яка не є істотною для вимірюваного зв’язку, що може привести до неправильно встановленого кількісного зв’язку між змінними; використання невідповідних аналітичних форм вибраних функцій для моделі, що як і при першій помилці специфікації може привести до зміщення оцінок параметрів моделі. Значення иі в матриці залишків и незалежні між собою і мають постійну дисперсію о2: М(ии') - а2Е, (6.6) де Е - одинична матриця; и' - матриця, транспонована до матриці и. Нагадаємо, що дисперсія відображає “розсіювання” випадкових значеньи,■ навколо їх математичного сподівання. Наявність сталої (постійної) дисперсії залишків називається гомоскедастичністю. Ця властивість може виконуватись лише тоді, коли залишки и є помилками вимірювання. Незалежні змінні моделі не пов’язані із залишками:
При порушенні цієї умови для оцінювання параметрів моделі використовуються не 1МНК, а інші методи, які будуть розглянуті пізніше. Незалежні змінні моделі утворюють незалежну систему векторів, тобто ці змінні незалежні між собою: Якщо незалежні змінні пов’язані між собою, то це явище називають мультиколінеарністю і воно є небажаним, так як робить оцінку параметрів за допомогою 1МНК ненадійною чутливою до вибраної специфікації моделі. Далі будуть розглянуті методи виявлення цього явища і способи його врахування. Оператор оцінювання 1МНК Скористаємося моделлю (4.1), для якої виконуються умови (4.2)–(4.5), щоб оцінити параметри методом 1МНК. Рівняння (4.1) подамо у вигляді:
Продиференціюємо цю умову за А і прирівняємо похідні до нуля:
або
Тут Звідси
Рівняння (4.6) дає матричну форму запису системи нормальних рівнянь, а формула (4.7) показує, що значення вектора А є розв’язком системи таких рівнянь. Формули (4.6) і (4.7) можна дістати й інакше. Так, помноживши рівняння (4.1) зліва спочатку на
Оскільки
Згідно з (4.4), коли
Неважко показати, що оцінки Â, обчислені за (4.7), мінімізують суму квадратів залишків u. При цьому значення вектору Â є розв’язком так званої системи нормальних рівнянь
Якщо незалежні змінні в матриці X взяті як відхилення кожного значення від свого середнього, то матрицю
Числа, що розміщені на її головній діагоналі, характеризують величину дисперсій незалежних змінних, інші елементи відповідають взаємним коваріаціям.Отже, структура матриці моментів відбиває зв’язки між незалежними змінними. Чим ближчі показники коваріацій до величини дисперсій, тим ближчий визначник матриці
|
||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 450; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.109.229 (0.012 с.) |

 Рис. 2.2. Кореляційне поле точок
Рис. 2.2. Кореляційне поле точок
 і
і 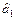 . Так, якщо витрати на споживання описуватимуться прямою I, то відхилення їх фактичних значень від розрахункових матимуть переважно знак «мінус». Якщо вони описуватимуться прямою III, то ці відхилення будуть переважно додатними, а якщо прямою II, то кількість від’ємних і додатних відхилень буде приблизно однаковою. Наявність серед відхилень переважно від’ємних чи додатних значень підтверджує, що вони мають невипадковий характер. А це означає: певна пряма лінія не адекватно описує фактичну залежність між витратами на споживання і доходом сімей. Звідси постає задача — застосувати метод найменших квадратів для оцінювання параметрів моделі, щоб відхилення фактичних витрат од розрахункових на основі прямої мали приблизно однакову суму від’ємних і додатних значень, а також були б найменшими. Останнє буде свідчити про те, що розрахункові значення витрат на споживання максимально наближені до фактичних, а це є гарантом вірогідності моделі.
. Так, якщо витрати на споживання описуватимуться прямою I, то відхилення їх фактичних значень від розрахункових матимуть переважно знак «мінус». Якщо вони описуватимуться прямою III, то ці відхилення будуть переважно додатними, а якщо прямою II, то кількість від’ємних і додатних відхилень буде приблизно однаковою. Наявність серед відхилень переважно від’ємних чи додатних значень підтверджує, що вони мають невипадковий характер. А це означає: певна пряма лінія не адекватно описує фактичну залежність між витратами на споживання і доходом сімей. Звідси постає задача — застосувати метод найменших квадратів для оцінювання параметрів моделі, щоб відхилення фактичних витрат од розрахункових на основі прямої мали приблизно однакову суму від’ємних і додатних значень, а також були б найменшими. Останнє буде свідчити про те, що розрахункові значення витрат на споживання максимально наближені до фактичних, а це є гарантом вірогідності моделі.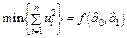 .
. найменша. Необхідна умова для цього — перетворення на нуль похідних цієї функції за кожним із параметрів
найменша. Необхідна умова для цього — перетворення на нуль похідних цієї функції за кожним із параметрів 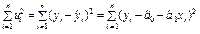 ,
,
 (2.19)
(2.19)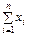 ,
,  ,
, 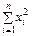 ,
,  , які можна дістати на підставі сукупності спостережень, і розв’яжемо її відносно невідомих параметрів
, які можна дістати на підставі сукупності спостережень, і розв’яжемо її відносно невідомих параметрів 

 ), то оцінки параметрів моделі можна знайти дещо інакше.
), то оцінки параметрів моделі можна знайти дещо інакше. .(2.20)
.(2.20) .
. ,
,  і
і 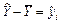 , тоді
, тоді ,
, .
. .
. . (2.21)
. (2.21) тобто друга похідна за параметром
тобто друга похідна за параметром  . (2.22)
. (2.22) М(Х и) - 0.
М(Х и) - 0.
 . Тоді суму квадратів залишків u можна записати так:
. Тоді суму квадратів залишків u можна записати так:

 (4.6)
(4.6) — матриця, транспонована до матриці незалежних змінних X.
— матриця, транспонована до матриці незалежних змінних X. (4.7)
(4.7) , дістанемо:
, дістанемо:
 то справджується рівність
то справджується рівність .
. ,
, 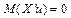 , отже,
, отже, (4.7)
(4.7) .
.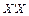 називають матрицею моментів.
називають матрицею моментів. до нуля і тим гірші оцінки параметрів
до нуля і тим гірші оцінки параметрів 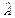 . Далі буде показано, що стандартні помилки параметрів
. Далі буде показано, що стандартні помилки параметрів  прямо пропорційні до значень, розміщених на головній діагоналі матриці
прямо пропорційні до значень, розміщених на головній діагоналі матриці 


