
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості оцінок параметрів лінійної моделі та їх інтерпретаціяСодержание книги
Поиск на нашем сайте Оцінки параметрів 1) незміщеності; 2) обгрунтованості; 3) ефективності; 4) інваріантності. Означення 4.5. Вибіркова оцінка параметрів
У розглядуваному випадку Оскільки згідно з першою умовою Незміщеність — це мінімальна вимога, яка ставиться до оцінок параметрів Різниця між математичним сподіванням оцінки і значенням оціненого параметра
називається зміщенням оцінки. Не можна плутати помилку оцінки з її зміщенням. Помилка дорівнює Дуже важливою властивістю оцінки є її обгрунтованість. Означення 4.6. Вибіркова оцінка
Іншими словами, оцінка обгрунтована, коли вона задовольняє закон великих чисел. Обгрунтованість помилки означає, що чим більші будуються вибірки, тим більша ймовірність того, що помилка оцінки не перевищуватиме достатньо малої величини e. Для обгрунтованості оцінок, здобутих на основі 1МНК, мають виконуватися три умови: 1) 2) 3) Третя властивість оцінок Â — ефективність — пов’язана з величиною дисперсії оцінок. Тут доречно сформулювати важливу теорему Гаусса — Маркова, що стосується ефективності оцінки 1МНК. Теорема Гаусса — Маркова. Функція оцінювання за методом 1МНК покомпонентно мінімізує дисперсію всіх лінійно незміщених функцій вектора оцінок
де Отже, функція оцінювання 1МНК З означення дисперсії випливає, що Означення 4.7. Вибіркова оцінка Нехай
тобто це відношення називається ефективністю оцінки. Очевидно, що Означення 4.8. Незміщена оцінка Пошук ефективних оцінок параметрів — досить складна справа. Проте оскільки дисперсія середнього арифметичного значення оцінки, яка має Ще одна важливість оцінок — їх інваріантність. Означення 4.8. Оцінка Інваріантність оцінок має велике практичне значення. Наприклад, якщо відома оцінка дисперсії генеральної сукупності і вона інваріантна, то оцінку середньоквадратичного відхилення можна дістати, добувши квадратний корінь із оцінки дисперсіі. Коефіцієнт кореляції R є інваріантною оцінкою до коефіцієнта детермінації 8. Дисперсійно-коваріаційна матриця, її обчислення та елементи У класичній регресійній моделі Y = XA + u вектор Відомо, що для характеристики випадкових змінних
Оцінки коваріаційної матриці Отже,
де
Оскільки вектор залишків
Звідси маємо альтернативну форму запису дисперсії залишків:
Позначимо (j, k)-й елемент матриці
Коваріації
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 613; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

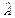 є вибірковими характеристиками і повинні мати такі властивості:
є вибірковими характеристиками і повинні мати такі властивості: називається незміщеною, якщо вона задовольняє рівність
називається незміщеною, якщо вона задовольняє рівність (4.12)
(4.12)
 , то
, то  . Отже, оцінка параметрів 1МНК є незміщеною.
. Отже, оцінка параметрів 1МНК є незміщеною. . Якщо оцінка незміщена, то при багаторазовому повторенні випадкової вибірки попри те, що для окремих вибірок, можливо, були помилки оцінки, середнє значення цих помилок дорівнює нулю.
. Якщо оцінка незміщена, то при багаторазовому повторенні випадкової вибірки попри те, що для окремих вибірок, можливо, були помилки оцінки, середнє значення цих помилок дорівнює нулю. (4.13)
(4.13) і є випадковою величиною, а зміщення — величина стала.
і є випадковою величиною, а зміщення — величина стала. параметрів А називається обгрунтованою, якщо при досить малій величині
параметрів А називається обгрунтованою, якщо при досить малій величині  > 0 справджується cпіввідношення
> 0 справджується cпіввідношення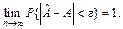 (4.14)
(4.14) , де Q — додатно визначена матриця;
, де Q — додатно визначена матриця;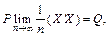 де Q — додатно визначена матриця;
де Q — додатно визначена матриця;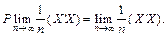
 для
для  ,
,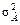 — дисперсія оцінок
— дисперсія оцінок  — дисперсія оцінок
— дисперсія оцінок 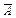 , визначених іншими методами.
, визначених іншими методами. — параметр розподілу випадкової величини А, яка є мірою розсіювання її значень навколо математичного сподівання.
— параметр розподілу випадкової величини А, яка є мірою розсіювання її значень навколо математичного сподівання. , а
, а  — деяка інша оцінка цих параметрів. Тоді
— деяка інша оцінка цих параметрів. Тоді (4.15)
(4.15) ; чим ближче
; чим ближче  до одиниці, тим ефективнішою є оцінка. Цікаво, що відношення може бути функцією сукупності спостережень
до одиниці, тим ефективнішою є оцінка. Цікаво, що відношення може бути функцією сукупності спостережень  , причому зі збільшенням
, причому зі збільшенням  задовольняє умову
задовольняє умову 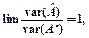 називається асимптотично ефективною оцінкою.
називається асимптотично ефективною оцінкою. вимірів, дорівнює
вимірів, дорівнює  то, як можна довести, що
то, як можна довести, що  дає ефективну оцінку параметрів А.
дає ефективну оцінку параметрів А. називається інваріантною, якщо для довільно заданої функції
називається інваріантною, якщо для довільно заданої функції  оцінка параметрів функції
оцінка параметрів функції  подається у вигляді
подається у вигляді  . Іншими словами, інваріантність оцінки базується на тому, що в разі перетворення параметрів
. Іншими словами, інваріантність оцінки базується на тому, що в разі перетворення параметрів 
 .
.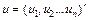 і залежний від нього вектор
і залежний від нього вектор 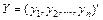 є випадковими змінними. До оператора оцінювання
є випадковими змінними. До оператора оцінювання  (
( ), а отже, оператор
), а отже, оператор  , поряд з математичним сподіванням, застосовуються також дисперсія
, поряд з математичним сподіванням, застосовуються також дисперсія  і коваріація
і коваріація  (j ¹ k). Істинні (справжні) значення цих параметрів класичної економетричної моделі утворюють дисперсійно-коваріаційну матрицю
(j ¹ k). Істинні (справжні) значення цих параметрів класичної економетричної моделі утворюють дисперсійно-коваріаційну матрицю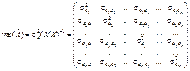 (4.16)
(4.16) використовуються для знаходження стандартних помилок та обчислення довірчих інтервалів оцінок параметрів
використовуються для знаходження стандартних помилок та обчислення довірчих інтервалів оцінок параметрів  містяться оцінки дисперсій
містяться оцінки дисперсій  j-ї оцінки параметрів, що ж до елементів
j-ї оцінки параметрів, що ж до елементів  (j ¹ k), які розміщені поза головною діагоналлю, то вони є оцінками коваріації між
(j ¹ k), які розміщені поза головною діагоналлю, то вони є оцінками коваріації між  .
. , (4.17)
, (4.17) — незміщена оцінка дисперсії залишків;
— незміщена оцінка дисперсії залишків; .
. , то добуток векторів
, то добуток векторів  можна записати так:
можна записати так: .
.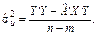
 символом
символом  , тоді j-й елемент по головній діагоналі матриці
, тоді j-й елемент по головній діагоналі матриці  . (4.18)
. (4.18) .(4.19)
.(4.19)


