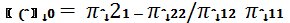Непрямий метод найменших квадратів оцінювання параметрів строго ідентифікованих рівнянь системи.

Для оцінювання параметрів системи структурних надідентифікованих рівнянь найбільш поширеними є двокроковий та трикроковий методи найменших квадратів.

Якщо рівняння моделі точно ідентифіковані, то непрямий і двокроковий методи дають однакову оцінку параметрів моделі. Якщо рівняння будуть надідентнфікованими, то ці оцінки будуть різними.

Таким чином, далі розглянемо непрямий метод найменших квадратів (НМНК).

Для точно ототожненого структурного рівняння можна отримати структурні параметри з МНК-оцінок коефіцієнтів зведеної форми методом, відомим під назвою метод непрямих найменших квадратів (ННК). Оцінка параметрів за цим методом умовно розбивається на такі три етапи.

1. Спочатку отримуємо рівняння зведеної форми. Для цього виражаємо залежну змінну в кожному рівнянні виключно через попередньо визначені (екзогенні та лагові) змінні та випадкові величини.

2. Окремо до кожного рівняння зведеної форми застосовуємо МНК. Це можливо, оскільки пояснювальні змінні в даних рівняннях попередньо визначені, а отже, некорельовані з випадковими величинами.

3. Отримуємо оцінки початкових структурних параметрів з оцінених на другому етапі коефіцієнтів зведеної форми. Якщо рівняння точно ототожнене, є взаємна відповідність між структурними параметрами та коефіцієнтами зведеної форми.

Розрахунок параметрів системи економетричних рівнянь попиту і пропозиції непрямим МНК.

Економічна теорія підказує, що коли нас цікавить співвідношення між ціною та кількістю, функцію попиту неможливо розглядати ізольовано. До аналізу потрібно включити функцію пропозиції. Розв’язок полягає у сумісному оцінюванні функцій попиту і пропозиції. Такі моделі відомі як системи одночасних рівнянь.

Q^d_t=a0+a1p_t+ a2y_t+ε_t^d,

Q^s_t=b0+b1p_t+a2z_t+ε_t^s, t=1,n

Q^s_t=Q^d_t,

Y-обсяг доходу, p-ціна товару, ε^{s -} хар-є зміну моделі внаслідок нецін факторів, z- осн нецін фактор пропоз. Класиф змінних: -ендогенні (визнач у рамках с-ми); -екзогенні. Для с-ми одночас р-нь має місце умова повноти: заг кіл-ть р-нь повинна співпад з кіл-тю ендогенних змінних.

Для систем таких рівнянь потрібно застосовувати спеціальні методи оцінювання, оскільки в них регрес ори корельовано зі збуреннями.

У структурному вигляді системи одночасних рівнянь кожне рівняння відображає певний елемент структури економічної системи, що розглядається, і має економічну інтерпретацію.

У зведеному вигляді в кожному рівнянні зліва стоїть ендогенна змінна, а справа – лише екзогенні змінні. Для знаходження коефіцієнтів, правильної ідентифікації та оцінки моделі необхідний зведений вигляд

У результаті деяких арифметичних перетворень та введення нових позначень ми зводимо сист структурних р-нь попиту і пропозиції до зведених.

P_t=π₁₁+ π₁₂y_t+ π₁₃z_t+v_t⁽¹⁾,

Q_t=π₂₁+ π₂₂y+ π₂₃z+v_t⁽²⁾ - сист р-нь зведеного виду.

Обидва р-ня системи є строго ідентифікованими:

1) К-сть ендогенних змінних у: Н=1, жодні змінна не вилучена з р-ня: D=0; D+1=Н;

2) Аналогічно

Якщо р-ня строго ідентифіковане, то для його оцінки використати непрямий МНК:

1. Скласти зведений вигляд моделі і визначити її коефіцієнти за доп. Звич. МНК;

2. Шляхом алгебраїчних перетворень повернутись до структурного вигляду сист. р-нь, отримуючи оцінки структурних параметрів.

У нашій системі

,,

 

Даля, підставляючи знайдені за МНК оцінки , t=1,2, j=0,2, отримуємо оцінки непрямого МНК: ,

, ,

Двоетапний МНК. Алгоритм.

Системою одночасних економетричних рівнянь називається сист, в якій одні і ті ж залежні змінні в одних рівняннях входять до лівої частини, а в інших – до правої частини. В них розрізняють: Ендогенні змінні – взаємозалежні змінні, які визначаються всередині моделі. Екзогенні змінні – незалежні змінні, які визначаються зовні системи. До групи предетермінованих змінних також включають лагові значення ендогенних змінних (значення ендогенних змінних в попередні моменти часу).

Двоетапний МНК використовується для оцінки надідентифікованих рівнянь у системах одночасних р-нь. Необхідна умова ідентифікації.

D + 1 = H – рівняння ідентифіковане, D + 1 < H – рівняння неідентифіковане,

D + 1 > H – рівняння надідентифіковане, де D – кількість предетермінов змінних, що відсутні в рів-ні, але присутні в системі,

H – кількість ендогенних змінних в рівнянні.

Алгоритм методу:

1. За допомогою звичайного методу найменших квадратів оцінюється регресія кожної ендогенної змінної відносно набору всіх екзогенних змінних системи.

2. Замість ендогенних змінних, що входять у праву частину рівняння, підставляються їх оцінки, знайдені на першому етапі. Одержані рівняння оцінюються за допомогою звичайного методу найменших квадратів.

Звичайний МНК: знаходження параметрів регресії:

Можна також скористатися готовими формулами:

Вибіркова регресійна функція має вигляд:

Залишки моделі знаходяться за формулою: