
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ТЕМА: Методи розв’язання алгебраїчних і трансцендентних рівняньСодержание книги
Поиск на нашем сайте
Розв’язання рівнянь – алгебраїчних і трансцендентних – являє собою одну з істотних задач прикладного аналізу, потреба в якій виникає в найрізноманітніших розділах фізики, техніки і природознавства. Задача визначення кореня рівняння з одним невідомим ƒ(x) = 0, (1.1) де ƒ(x) – безперервна функція, складається з двох етапів: 1) відділення кореня, тобто визначення числового проміжку, у якому міститься один корінь рівняння; 2) уточнення значення кореня шляхом побудови послідовності xк = φ (xк-1), к = 1, 2, 3,... на основі відповідного методу. Для уточнення значення кореня існують різні ітераційні методи. 1.1 Відділення числового проміжку, у якому міститься один корінь рівняння 1.1.1 Відділення кореня графічно (перший спосіб) Якщо рівняння (1.1) зручно представити у вигляді g (х) – h (х), (1.2) то абсцису х0 точки перетинання графіків у = g(х) і у = h (х) можна знайти по кресленню. Величину х0 визначити з достатньою точністю графічно не можливо. Тому варто вибрати такий числовий проміжок [a; b] для якого свідомо виконується нерівність a ≤ х0 ≤ b. Різні знаки функції при х =а і х = b ƒ(а) * ƒ(b) ≤ 0 (1.3) свідчать про наявність кореня в проміжку [a; b].
Другий спосіб відділення кореня Цей спосіб містить звичайне табулювання функції у = ƒ (х) на інтервалі існування функції, при цьому ступінь зміни аргументу підбирається значимим. І знову, різні знаки функції при х =а і х = b, тобто ƒ(а) * ƒ(b) ≤ 0 свідчать про наявність кореня в проміжку [a; b]. 1.2 Уточнення значення кореня рівняння ƒ(x) = 0
Метод половинного ділення (метод бісекцій) Умова застосовності методу половинного ділення припускає безперервність функції ƒ (х) на проміжку [a; b]. Уточнення значення кореня проводиться шляхом побудови послідовності, що сходиться
xк =(ак + bк) / 2, к = 1, 2, (1.4)
За а1, b1 приймаємо відповідно а, b. Припускаючи, що наближення xn (де n – фіксоване значення к) відомо, для знаходження xn+1 вибираємо наступні значення an+1, bn+1 в залежності від знака добутку f(an ) * f(xn). Якщо f(an ) * f(xn) < 0, то bn+1 вважаємо рівним знайденому значенню xn і an+1 рівними an, інакше bn+1 = bn, an+1 = xn. На рис. 1.1 зображена поведінка послідовних наближень у випадку ƒ(а) < 0, ƒ(b) > 0.
Рисунок 1.1 – Графічне зображення методу бісекцій
Рішення рівняння (1.1) вважається знайденим з точністю Е, якщо виконається умова | хк + 1 – хк | < Е (1.5) Метод хорд (метод пропорційних чисел) Умови збіжності методу припускають, що ƒ ' (x) і ƒ '' (x) зберігають знак на проміжку [a; b]. Побудова послідовності, що сходиться, проводиться по формулі хк = хк – 1 - ƒ(хк – 1) * (с - хк – 1) / (ƒ(с) - ƒ(хк – 1)), к = 1, 2,... (1.6) де с – нерухомий кінець проміжку. Якщо ƒ(а) * ƒ '' (а) > 0, то за нерухомий кінець приймається а, тоді х0 = b. У противному випадку, нерухомий кінець b, а як нульове наближення вибирається а. На рис. 1.2 зображене поводження послідовних наближень у випадках: а) ƒ(а) > 0, ƒ '' (а) > 0; б) ƒ(а) < 0, ƒ '' (а) < 0.
Рисунок 1.2 – Графічне зображення методу хорд (послідовні наближення)
Процес наближення відбувається до виконання умови (1.5), або доки ƒ(хк) | ≤ Е (1.7)
Метод Ньютона (метод дотичних) Умови збіжності методу припускають, що ƒ ' (x) і ƒ '' (x) зберігають знак на проміжку [a; b]. Уточнення значення кореня проводиться шляхом побудови збіжності послідовності. хк = хк – 1 - ƒ(хк – 1) / ƒ ' (хк – 1), к = 1, 2, 3,... (1.8) За х0 приймаємо той з кінців проміжку [a; b], на якому виконується умова ƒ(х0) * ƒ''(х0) > 0 (1.9) Поведінка послідовних наближень при ƒ(а) < 0, ƒ '' (а) < 0 (а); ƒ(а) > 0, ƒ '' (а) > 0 (б) ілюструється на рис. 1.3.
Рисунок 1.3 – Графічне відображення методу дотичних Процес наближення відбувається до виконання умови (1.5), або (1.7). 1.2.4 Використання пакету аналізу „что - если” Excel Чисельний аналіз даних зазвичай відбувається через меню „Сервис”. Інструмент „Подбор параметра” дозволяє знайти значення аргументу, задовольняючого наданому значенню функції. Якщо необхідно вирішити рівняння ƒ(x) = 0, треба визначити адресу клітини, куди буде занесене початкове значення кореня. Саме рівняння ƒ(x) записується в іншій клітині з посиланням на першу. У вікні „Подбор параметра” вказуємо початкові значення параметрів, зразок на рис.1.4.
Рисунок 1.4 – Вікно „Подбор параметра”
Для уточнювання знайденого рішення потрібно в меню „Сервис / Параметри” на вкладниці „Вычисления” змінити значення відповідних параметрів: кількість ітерацій; погрішність.
Індивідуальні завдання Для кожної функції визначити числовий проміжок у якому міститься один корінь рівняння, уточнити значення кореня вказаними вище методами. 1.3.1 1.3.2 1) 2) 3) 4) 1.3.3 1.3.4 1) 2) 3) 4)
1.3.5 1.3.6 1) 2) 3) 4) 1.3.7 1.3.8 1) 2) 3) 4) 1.3.9 1.3.10 1) 2) 3) 4) 1.3.11 1.3.12 1) 2) 3) 4) 1.3.13 1.3.14 1) 2) 3) 4) 1.3.15 1.3.16 1) 2) 3) 4) 1.3.17 1.3.18 1) 2) 3) 4) 1.3.19 1.3.20 1) 2) 3) 4) 1.3.21 1.3.22 1) 2) 3) 4)
1.3.23 1.3.24 1) 2) 3) 4) 1.3.25 1.3.26 1) 2) 3) 4) 1.3.27 1.3.28 1) 2) 3) 4) 1.3.29 1.3.30 1) 2) 3) 4)
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 319; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.206.218 (0.009 с.) |





 ; 1)
; 1)  ;
; ; 2)
; 2) 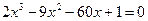 ;
;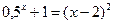 ; 3)
; 3)  ;
; ,
,  . 4)
. 4) 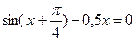 .
. ; 1)
; 1)  ;
; ; 2)
; 2)  ;
; ; 3)
; 3)  ;
; . 4)
. 4)  .
. ; 1)
; 1)  ;
;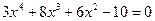 ; 2)
; 2)  ;
; ; 3)
; 3)  ;
; . 4)
. 4)  ,
, 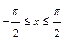 .
. ; 1)
; 1)  ;
; ; 2)
; 2) 
 ; 3)
; 3)  ;
; . 4)
. 4)  .
. ; 1)
; 1)  ;
; ; 2)
; 2)  ;
;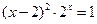 ; 3)
; 3)  ;
; . 4)
. 4)  .
. ; 1)
; 1)  ;
; ; 2)
; 2)  ;
; ; 3)
; 3) 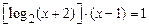 ;
; ,
, 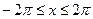 . 4)
. 4)  .
.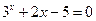 ; 1)
; 1)  ;
; ; 2)
; 2)  ; 3)
; 3)  ;
; . 4)
. 4) 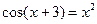 .
. ; 1)
; 1)  ;
; ; 3)
; 3)  ;
;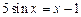 . 4)
. 4)  ,.
,.  ; 1)
; 1) 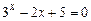 ;
;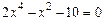 ; 2)
; 2) 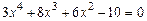 ;
; ; 3)
; 3) 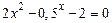 ;
;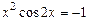 ,
,  .
. ; 1)
; 1)  ;
; ;
; ; 1)
; 1)  ;
; ; 2)
; 2) 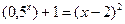 ; 3)
; 3)  ;
; ,
,  .
. ; 1)
; 1)  ;
; ; 3)
; 3)  ;
; ; 1)
; 1)  ;
; ; 2)
; 2)  ;
;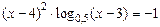 ; 3)
; 3)  ;
; . 4)
. 4)  ,
,  ; 1)
; 1)  ;
;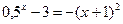 ; 3)
; 3)  ;
; ;
; . 4)
. 4)  ,
, 



