
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення параметрів емпіричних формул по способу найменших квадратів у випадку лінійної залежностіСодержание книги
Поиск на нашем сайте Нехай необхідно установити залежність між двома величинами x і y. Зробимо n вимірів і результати занесемо в таблицю
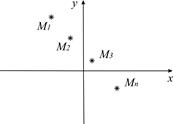
Будемо розглядати xі і yі як прямокутні декартові координати точок на площі: M1(x1, y1), M2(x2, y2),..., Mn(xn, yn) Припустимо, що ці точки майже лежать на деякій прямій, як показано на рис. 5.1, отже, між x і y існує лінійна залежність, тобто y=ax+b, (5.1) де a, b – const і їх необхідно визначити.
Рисунок 5.1 – Зображення точок на площині Точки Mi(xі, yi) тільки приблизно лежать на прямій, отже, і формули є наближеними. Таким чином, якщо підставити у формулу ах + b – у = 0 координати xi, yi з таблиці, то одержуємо рівності:
де Потрібно підібрати коефіцієнти a і b так, щоб відхилення були по можливості малими по абсолютній величині. Відповідно до методу найменших квадратів, підберемо коефіцієнти a і b так, щоб сума квадратів відхилень
була найменшою. Підставляючи рівності (5.2) у формулу (5.3) одержуємо:
Змінна величина U є функцією двох змінних a і b, де a і b необхідно визначити; xi і yi - змінні, отримані в результаті вимірів. Підберемо параметри a і b так, щоб функція U одержала можливо менше значення, тобто
Знайдемо частки похідні функції U по a і b, дорівняємо їх нулю, одержимо нормальну систему:
Із системи (5.5) визначають параметри a і b емпіричної формули (5.1).
Визначення параметрів емпіричних формул по способу найменших квадратів у випадку нелінійної залежності Цей спосіб може привести до системи лінійних або до системи нелінійних рівнянь. Частково ця задача може бути вирішена графічними засобами Excel, коли до побудованого графіку добавляють лінію тренду з відповідними аналітичним виразом.
Індивідуальні завдання
Скористатися визначеною функцією, яка задана таблицею, лабораторної роботи №4, та наблизити її по методу найменших квадратів лінійною залежністю. Для цієї ж таблиці підібрати нелінійну залежність, яка кращим чином описує таблицю. Відобразити всі графіки.
Приклад виконання лабораторної роботи
Результати вимірів величин представлені у вигляді таблиці:
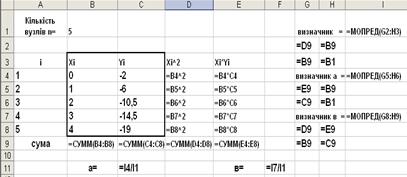
Розташуємо цю таблицю на листі Excel, як на рис. 5.2.
Рисунок 5.2 – Вид таблиці на листі Excel Відповідний протокол рішення має вигляд, як на рис. 5.3.
Рисунок 5.3 – Протокол рішення лінійної залежності
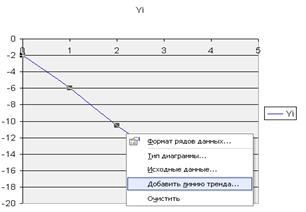
Згідно з протоколом рішення, шукана лінійна залежність: y = - 4,25x - 1,9. Для підбору нелінійної залежності побудуємо графік y = f(x),для чого виділяємо 2 стовпчика (В3:С8). Скористаємось майстром діаграм. На першому кроці вибираємо тип діаграми „точечная”. Після побудови графіка добавимо лінію тренда (апроксимуючу функцію). Поетапне додавання лінії тренда показано на рис. 5.4, рис. 5.5, рис. 5.6.
Рисунок 5.4 – Крок перший: „Добавить линию тренда”
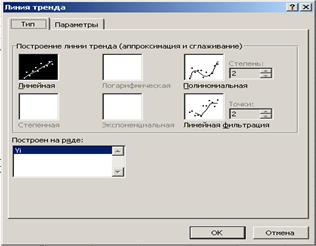
Рисунок 5.5 – Крок другий: „Выбор типа”
Рисунок 5.6 – Крок третій: „Параметры: показывать уравнение на диаграме”
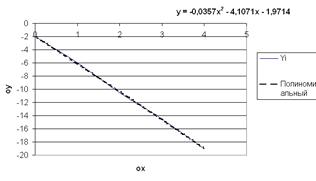
Протокол рішення побудови лінії тренда має вигляд, як на рис. 5.7.
Рисунок 5.7 – Протокол рішення побудови лінії тренда ЛАБОРАТОРНА РОБОТА № 6 ТЕМА: Наближені методи розв’язку звичайних диференційних рівнянь 6.1. Теоретичні відомості
Розв’язання задачі Коши для диференційного рівняння
полягає в пошуку функції у(х), що задовольняє рівнянню (6.1) та початковій умові у(х0) = у0, (6.2) де х0, у0 – надані числа. Чисельні методи надають розв’язок задачі у вигляді таблиці функції у(х) на даному інтервалі [a, b]. Для розв’язання означеної задачі застосовують наступні методи: а) Метод Ейлера для рівняння (6.1) з умовою (6.2) обчислює таблицю значень yi = y(xi),
де xi = x0 + ih (і = 0, 1, 2, …, n), h = (b-a) / n, [a, b] – інтервал, на якому шукається рішення. Значення уі+1 розраховується за формулою
yi+1 = yi + hƒ(xi, yi) (і = 0, 1, 2, …, n).
б) Метод Рунге-Кутта: на кожному кроці обчислювання виконується за формулою
де
Індивідуальні завдання Застосовуючи два чисельні методи (Ейлера, Рунге-Кутта) знайти розв’язок нелінійного диференційного рівняння першого порядку (задача Коши). Розв’язок обчислити на даному інтервалі [a, b]. Кількість кроків інтегрування вибрати з інтервалу 30 – 50. За отриманою таблицею побудувати графіки цієї функції та з’ясувати вид лінії тренду.
6.2.1
6.2.2
6.2.3
6.2.4
6.2.5
6.2.6
6.2.7
6.2.8
6.2.9
6.2.10
6.2.11
6.2.12
6.2.13
6.2.14
6.2.15
6.2.16
6.2.17
6.2.18
6.2.19
6.2.20
6.2.21
6.2.22
6.2.23
6.2.24
6.2.25
6.2.26
6.2.27
6.2.28
6.2.29
6.2.30
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 384; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 , (5.2)
, (5.2)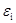 - відхилення.
- відхилення.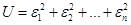 (5.3)
(5.3)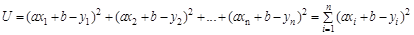 (5.4)
(5.4)
 (5.5)
(5.5)


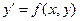 (6.1)
(6.1) ,
, ;
; 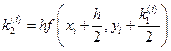
 ;
;  .
. ; у0(1,8) = 2,6; х є [1,8; 2,8]
; у0(1,8) = 2,6; х є [1,8; 2,8] ; у0(0) = 0; х є [0; 20]
; у0(0) = 0; х є [0; 20]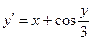 ; у0(1,6) = 4,6; х є [1,6; 2,6]
; у0(1,6) = 4,6; х є [1,6; 2,6] ; у0(0) = 1; х є [0; 2]
; у0(0) = 1; х є [0; 2] ; у0(1,8) = 2,6; х є [1,8; 2,8]
; у0(1,8) = 2,6; х є [1,8; 2,8]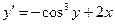 ; у0(-2) = 1; х є [-2; 2]
; у0(-2) = 1; х є [-2; 2]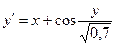 ; у0(0,9) = 1,7; х є [0,9; 1,9]
; у0(0,9) = 1,7; х є [0,9; 1,9]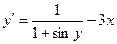 ; у0(0) = 1; х є [0; 3]
; у0(0) = 1; х є [0; 3]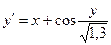 ; у0(1,2) = 1,8; х є [1,2; 2,2]
; у0(1,2) = 1,8; х є [1,2; 2,2]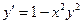 ; у0(0) = 1; х є [0; 3]
; у0(0) = 1; х є [0; 3]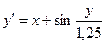 ; у0(0,5) = 1,8; х є [0,5; 1,5]
; у0(0,5) = 1,8; х є [0,5; 1,5] ; у0(0) = 0; х є [0; 10]
; у0(0) = 0; х є [0; 10] ; у0(0,3) = 0,9; х є [0,3; 1,3]
; у0(0,3) = 0,9; х є [0,3; 1,3] ; у0(0) = 1; х є [0; 5]
; у0(0) = 1; х є [0; 5] ; у0(1,2) = 1,4; х є [1,2; 2,2]
; у0(1,2) = 1,4; х є [1,2; 2,2]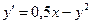 ; у0(0) = 1; х є [0; 5]
; у0(0) = 1; х є [0; 5]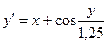 ; у0(0,4) = 0,8; х є [0,4; 1,4]
; у0(0,4) = 0,8; х є [0,4; 1,4] ; у0(0) = 1; х є [0; 10]
; у0(0) = 1; х є [0; 10]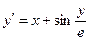 ; у0(1,4) = 2,5; х є [1,4; 2,4]
; у0(1,4) = 2,5; х є [1,4; 2,4] ; у0(0) = 0; х є [0; 15]
; у0(0) = 0; х є [0; 15] ; у0(1,7) = 5,3; х є [1,7; 2,7]
; у0(1,7) = 5,3; х є [1,7; 2,7]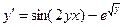 ; у0(0) = 0; х є [0; 15]
; у0(0) = 0; х є [0; 15]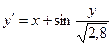 ; у0(1,4) = 2,2; х є [1,4; 2,4]
; у0(1,4) = 2,2; х є [1,4; 2,4] ; у0(0) = 0; х є [0; 1]
; у0(0) = 0; х є [0; 1]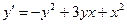 ; у0(0) = 0; х є [0; 5]
; у0(0) = 0; х є [0; 5]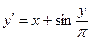 ; у0(1,7) = 5,3; х є [1,7; 2,7]
; у0(1,7) = 5,3; х є [1,7; 2,7]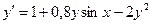 ; у0(0) = 0; х є [0; 1]
; у0(0) = 0; х є [0; 1] ; у0(0,2) = 0,25; х є [0,2; 1,2]
; у0(0,2) = 0,25; х є [0,2; 1,2] ; у0(0) = 0; х є [0; 1]
; у0(0) = 0; х є [0; 1]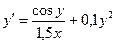 ; у0(0) = 0; х є [0; 1]
; у0(0) = 0; х є [0; 1]


