
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методичні вказівки та завданняСодержание книги Поиск на нашем сайте
МЕТОДИЧНІ ВКАЗІВКИ ТА ЗАВДАННЯ до лабораторних та самостійних робіт з курсів „Основи інформатики та обчислювальної техніки” та „Алгоритмічні мови та програмне забезпечення” за темою „Чисельні методи в інженерних розрахунках”
для студентів технічних спеціальностей денної форми навчання
Методичні вказівки та завдання до лабораторних та самостійних робіт з курсів „Основи інформатики та обчислювальної техніки” та „Алгоритмічні мови та програмне забезпечення” за темою „Чисельні методи в інженерних розрахунках” для студентів технічних спеціальностей денної форми навчання /Укл.:В.Г.Вишневська, О.В.Корнєєва, Г.В.Романіченко, Л.І.Лозовська, К.В.Пугіна. – Запоріжжя: ЗНТУ,2005. – 65с.
Методичні вказівки містять індивідуальні завдання та теоретичні відомості до лабораторних робіт з курсів „Основи інформатики та обчислювальної техніки” та „Алгоритмічні мови та програмне забезпечення”, приклади їх виконання з використанням середовища Excel та програмування мовою VBA для студентів технічних спеціальностей денної форми навчання.
Укладачі: В.Г. Вишневська, доцент, О.В. Корнєєва, асистент, Г.В. Романіченко, асистент, Л.І. Лозовська, доцент, К.В. Пугіна, аспірант.
Рецензенти: Н.І. Біла, доцент, О.І. Денисенко, доцент.
Експерт: А.О. Шумілов, к.т.н., доцент.
Відповідальний за випуск Г.В. Корніч, професор.
Затверджено на засіданні кафедри обчислювальної математики протокол № 8 від 29.04.05 р. ЗМІСТ
1 Лабораторна робота №1: Методи розв’язання алгебраїчних і трансцендентних рівнянь.......................................................................... 5 1.1 Відділення числового проміжку, у якому міститься один корінь рівняння...................................................................................................... 5 1.1.1 Відділення кореня графічно (перший спосіб)..................... 5 1.1.2Другий спосіб відділення кореня......................................... 6 1.2 Уточнення значення кореня рівняння ƒ(x) = 0........................... 6 1.2.1 Метод половинного ділення (метод бісекцій).................... 6 1.2.2 Метод хорд (метод пропорційних чисел)............................ 6 1.2.3 Метод Ньютона (метод дотичних)....................................... 7 1.2.4 Використання пакету аналізу „что - если” Excel................ 8 1.3 Індивідуальні завдання.................................................................. 8 1.4 Приклади виконання лабораторної роботи............................... 12 2 Лабораторна робота №2: Методи розв’язання систем нелінійних рівнянь...................................................................................................... 21 2.1 Відділення першого наближення до рішення............................ 21 2.2 Методи уточнення рішення системи нелінійних рівнянь....... 21 2.2.1 Метод ітерацій...................................................................... 21 2.2.2 Використання пакету аналізу Excel................................... 22 2.3 Індивідуальні завдання................................................................ 23 2.4 Приклади виконання лабораторної роботи............................... 27 3 Лабораторна робота №3: Обчислення інтегралів............................ 33 3.1 Теоретичні відомості................................................................... 33 3.2 Індивідуальні завдання................................................................ 34 3.3 Приклади виконання лабораторної роботи............................... 38 4 Лабораторна робота №4: Наближення (інтерполяція) функцій...... 42 4.1 Теоретичні відомості................................................................... 42 4.2 Індивідуальні завдання............................................................... 43 4.3 Приклади виконання лабораторної роботи............................... 48 5 Лабораторна робота №5: Апроксимація даних (емпіричні формули).................................................................................................. 51 5.1 Теоретичні відомості.................................................................. 51 5.1.1 Визначення параметрів емпіричних формул по способу найменших квадратів у випадку лінійної залежності......................... 51 5.1.2 Визначення параметрів емпіричних формул по способу найменших квадратів у випадку нелінійної залежності...................... 53 5.2 Індивідуальні завдання................................................................ 53 5.3 Приклад виконання лабораторної роботи.................................. 53 6 Лабораторна робота №6: Визначення параметрів емпіричних формул по способу найменших квадратів у випадку нелінійної залежності................................................................................................ 57 6.1 Теоретичні відомості................................................................... 57 6.2 Індивідуальні завдання................................................................ 58 6.3 Приклад виконання лабораторної роботи..................................61 6.3.1 Метод Ейлера........................................................................61 6.3.2 Метод Рунге-Кутта...............................................................62 7 Література............................................................................................ 64 8 Вимоги до оформлення лабораторної роботи................................... 64 8.1 Додаток А...................................................................................... 65 ЛАБОРАТОРНА РОБОТА № 1 ТЕМА: Методи розв’язання алгебраїчних і трансцендентних рівнянь Розв’язання рівнянь – алгебраїчних і трансцендентних – являє собою одну з істотних задач прикладного аналізу, потреба в якій виникає в найрізноманітніших розділах фізики, техніки і природознавства. Задача визначення кореня рівняння з одним невідомим ƒ(x) = 0, (1.1) де ƒ(x) – безперервна функція, складається з двох етапів: 1) відділення кореня, тобто визначення числового проміжку, у якому міститься один корінь рівняння; 2) уточнення значення кореня шляхом побудови послідовності xк = φ (xк-1), к = 1, 2, 3,... на основі відповідного методу. Для уточнення значення кореня існують різні ітераційні методи. 1.1 Відділення числового проміжку, у якому міститься один корінь рівняння 1.1.1 Відділення кореня графічно (перший спосіб) Якщо рівняння (1.1) зручно представити у вигляді g (х) – h (х), (1.2) то абсцису х0 точки перетинання графіків у = g(х) і у = h (х) можна знайти по кресленню. Величину х0 визначити з достатньою точністю графічно не можливо. Тому варто вибрати такий числовий проміжок [a; b] для якого свідомо виконується нерівність a ≤ х0 ≤ b. Різні знаки функції при х =а і х = b ƒ(а) * ƒ(b) ≤ 0 (1.3) свідчать про наявність кореня в проміжку [a; b].
Другий спосіб відділення кореня Цей спосіб містить звичайне табулювання функції у = ƒ (х) на інтервалі існування функції, при цьому ступінь зміни аргументу підбирається значимим. І знову, різні знаки функції при х =а і х = b, тобто ƒ(а) * ƒ(b) ≤ 0 свідчать про наявність кореня в проміжку [a; b]. 1.2 Уточнення значення кореня рівняння ƒ(x) = 0
Індивідуальні завдання Для кожної функції визначити числовий проміжок у якому міститься один корінь рівняння, уточнити значення кореня вказаними вище методами. 1.3.1 1.3.2 1) 2) 3) 4) 1.3.3 1.3.4 1) 2) 3) 4)
1.3.5 1.3.6 1) 2) 3) 4) 1.3.7 1.3.8 1) 2) 3) 4) 1.3.9 1.3.10 1) 2) 3) 4) 1.3.11 1.3.12 1) 2) 3) 4) 1.3.13 1.3.14 1) 2) 3) 4) 1.3.15 1.3.16 1) 2) 3) 4) 1.3.17 1.3.18 1) 2) 3) 4) 1.3.19 1.3.20 1) 2) 3) 4) 1.3.21 1.3.22 1) 2) 3) 4)
1.3.23 1.3.24 1) 2) 3) 4) 1.3.25 1.3.26 1) 2) 3) 4) 1.3.27 1.3.28 1) 2) 3) 4) 1.3.29 1.3.30 1) 2) 3) 4) ЛАБОРАТОРНА РОБОТА № 2 Метод ітерацій Зведемо систему (2.1) до вигляду
по встановленому початковому наближенню до рішення х0, у0, уточнення рішення відбувається за формулами:
Умови збіжності методу припускають, що
Рішення системи (2.1) вважається знайденим з точністю ε, якщо виконуються умови:
Індивідуальні завдання Для кожної системи нелінійних рівнянь визначити початкове наближення до рішення та уточнити це рішення з точністю ε = 0,001.
2.3.1 1)
2.3.2 1)
2.3.3 1) 2.3.4 1)
2.3.5 1)
2.3.6 1) 2.3.7 1)
2.3.8 1) 2.3.9 1) 2.3.10 1) 2.3.11 1) 2.3.12 1) 2.3.13 1) 2.3.14 1) 2.3.15 1) 2.3.16 1) 2.3.17 1) 2.3.18 1) 2.3.19 1) 2.3.20 1) 2.3.21 1) 2.3.22 1) 2.3.23 1) 2.3.24 1) 2.3.25 1) 2.3.26 1) 2.3.27 1) 2.3.28 1) 2.3.29 1) 2.3.30 1) ЛАБОРАТОРНА РОБОТА № 3 ТЕМА: Обчислення інтегралів 3.1 Теоретичні відомості
Точне обчислення визначеного інтеграла за формулою Ньютона-Лейбниця не завжди представляється можливим чи доцільним. У цих випадках, а також у випадках, коли підінтегральна функція задана табличним способом, доцільно проводити обчислювання приблизно. До найпростіших методів відносяться формула прямокутників, формула парабол (Сімпсона). При обчисленнях за формулами прямокутників результати будуть тим точніші, чим більше число відрізків розбивки проміжку інтегрування. Найпростіша - формула лівих прямокутників:
де Для забезпечення наданої степені точності ε значення n визначається за умовою:
За формулою парабол маємо:
де Згідно екстраполяції по Річардсону більш точне значення інтеграла можна визначити за формулою:
де
Індивідуальні завдання Для кожного варіанту: 1) обчислити інтеграл по формулі прямокутників з точністю ε = 0,01; 2) по формулі парабол обчислити інтеграл, уточнювання провести згідно формулі Річардсона.
3.2.1 1)
3.2.2 1)
3.2.3 1) 3.2.4 1)
3.2.5 1) 3.2.6 1) 3.2.7 1) 3.2.8 1) 3.2.9 1) 3.2.10 1) 3.2.11 1) 3.2.12 1) 3.2.13 1) 3.2.14 1) 3.2.15 1) 3.2.16 1) 3.2.17 1) 3.2.18 1) 3.2.19 1) 3.2.20 1) 3.2.21 1) 3.2.22 1) 3.2.23 1) 3.2.24 1) 3.2.25 1) 3.2.26 1) 3.2.27 1) 3.2.28 1) 3.2.29 1) 3.2.30 1)
3.3 Приклади виконання лабораторної роботи
Приклад 3.3.1 Обчислити інтеграл
Вирішимо задачу, використовуючи середовище Excel. Треба обчислити функцію Кількість відрізків розбивки проміжку інтегрування визначимо з умови (3.2):
М=2, тоді Розмістимо початкові значення та таблицю значень x, у у такому вигляді, як показано на рис. 3.1.
Рисунок 3.1 – Таблиця початкових значень та значень х, у
Згідно протоколу рішення, який показано на рис. 3.2, отримаємо відповідь:
Рисунок 3.2 – Протокол рішення інтегралу за формулою прямокутників
Приклад 3.3.2 Обчислити інтеграл парабол, уточнювання провести згідно формули Річардсона. Для вирішення задачі з’ясуємо початкові дані: a = 1,2; b = 1,6,
Рисунок 3.3 – Зразок листа Excel з ім’ям „Сімпсона”
Текст процедури:
Зразок протоколу рішення наведено на рис. 3.4.
Рисунок 3.4 – Протокол рішення інтегралу за формулою парабол
Згідно протоколу рішення маємо:
ЛАБОРАТОРНА РОБОТА №4 Теоретичні відомості Задача наближення функції виникає, коли для функції, даної при дискретних значеннях аргументу у вигляді таблиці (ці значення називаються вузлами інтерполяції) необхідно знайти значення функції в проміжних крапках. Накладаючи вимогу, щоб наближена функція у вузлах співпадала з табличними значеннями (рис. 4.1), одержуємо задачу інтерполяції.
Рисунок 4.1 – Графік наближеної функції
Нехай в результаті спостережень за ходом деякого процесу побудована таблиця:
Тобто, функція f(x) задана таблицею значень для кінцевої безлічі значень х. Якщо необхідно знайти значення f(x) для проміжного значення аргументу, то будують функцію φ(x), просту для обчислень і таку, що для заданих x0, x1, x2,..., xn приймає значення f(x0), f(x1), f(x2),..., f(xn). В інших точках відрізка [x0, xn] вважаємо, що φ(x) приблизно визначає функцію f(x) з тим чи іншим ступенем точності. Найчастіше, функцію φ(x) представляють у вигляді алгебраїчного багаточлена деякого ступеня. Найпростіша інтерполяція – це лінійна, тобто, коли невідому аналітичну залежність f(x) замінюють відрізками прямих, які проходять через відповідні вузли інтерполяції. В цьому випадку потрібно визначити якому відрізку належить надане х* і за формулою лінійної інтерполяції знаходять f(x*). Якщо xi <= x* <= xi+1, то відповідна пряма проходить через вузли (xi, f(xі)), (xi+1, f(xі+1)):
Точність підрахунків в цьому випадку незначна, тому що враховується вплив тільки 2-ох вузлів інтерполяції. Частіше будують багаточлен Pn(x) ступеня n, що в (n+1) даних точках x0, x1, x2,..., xn. приймає дані значення y0 = f(x0), y1 = f(x1), …, yn = f(xn), тобто f(xі) = Pn(xі), (і = 0, 1, 2,..., n). Відзначимо, що двох різних інтерполяційних багаточленів одного і того же ступеня n існувати не може. Цим умовам задовольняє інтерполяційний багаточлен Лагранжа:
Тоді
Індивідуальні завдання
Для кожного варіанту обчислити наближене значення функції, яка задана таблицею, для наданого х*, використовуючи лінійну інтерполяцію по Лагранжу.
4.2.1 х* = 1,50
4.2.2 х* = 0,45
4.2.3 х* = 0,66
4.2.4 х* = 3,2
4.2.5 х* = 3,50
4.2.6 х* = 0,85
4.2.7 х* = 1,74
4.2.8 х* = 4,51
4.2.9 х* = 1,90
4.2.10 х* = 3,82
4.2.11 х* = 2,22
4.2.12 х* = 5,32
4.2.13 х* = 1,35
4.2.14 х* = 0,80
4.2.15 х* = 2,85
4.2.16 х* = 0,60
4.2.17 х* = 1,52
4.2.18 х* = 3,50
4.2.19 х* = 1,44
4.2.20 х* = 0,56
4.2.21 х* = 1,82
4.2.22 х* = 2,50
4.2.23 х* = 3,35
4.2.24 х* = 1,50
4.2.25 х* = 1,56
4.2.26 х* = 1,08
4.2.27 х* = 3,33
4.2.28 х* = 1,44
4.2.29 х* = 1,50
|

 ; 1)
; 1)  ;
; ; 2)
; 2) 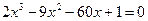 ;
;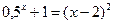 ; 3)
; 3)  ;
; ,
,  . 4)
. 4) 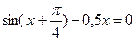 .
. ; 1)
; 1)  ;
; ; 2)
; 2)  ;
; ; 3)
; 3)  ;
; . 4)
. 4)  .
. ; 1)
; 1)  ;
;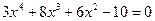 ; 2)
; 2)  ;
; ; 3)
; 3)  ;
; . 4)
. 4)  ,
, 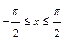 .
. ; 1)
; 1)  ;
; ; 2)
; 2) 
 ; 3)
; 3)  ;
; . 4)
. 4)  .
. ; 1)
; 1)  ;
; ; 2)
; 2)  ;
;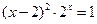 ; 3)
; 3)  ;
; . 4)
. 4)  .
. ; 1)
; 1)  ;
; ; 2)
; 2)  ;
; ; 3)
; 3) 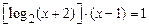 ;
; ,
, 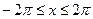 . 4)
. 4)  .
.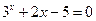 ; 1)
; 1)  ;
; ; 2)
; 2)  ; 3)
; 3)  ;
; . 4)
. 4) 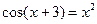 .
. ; 1)
; 1)  ;
; ; 3)
; 3)  ;
;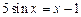 . 4)
. 4)  ,.
,.  ; 1)
; 1) 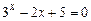 ;
;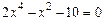 ; 2)
; 2) 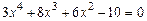 ;
; ; 3)
; 3) 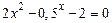 ;
;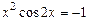 ,
,  .
. ; 1)
; 1)  ;
; ;
; ; 1)
; 1)  ;
; ; 2)
; 2) 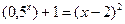 ; 3)
; 3)  ;
; ,
,  .
. ; 1)
; 1)  ;
; ; 3)
; 3)  ;
; ; 1)
; 1)  ;
; ; 2)
; 2)  ;
;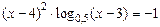 ; 3)
; 3)  ;
; . 4)
. 4)  ,
,  ; 1)
; 1)  ;
;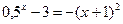 ; 3)
; 3)  ;
; ;
; . 4)
. 4)  ,
, 
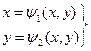 , (2.3)
, (2.3)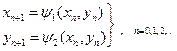 (2.4)
(2.4)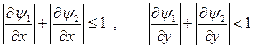 (2.5)
(2.5)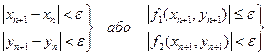
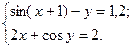 2)
2) 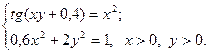
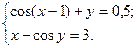 2)
2) 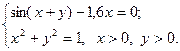
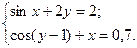 2)
2) 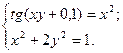
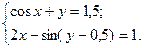 2)
2) 
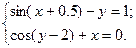 2)
2) 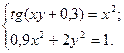
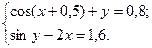 2)
2) 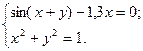
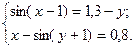 2)
2) 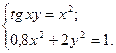
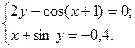 2)
2) 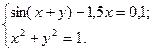
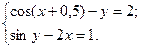 2)
2) 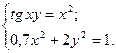
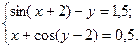 2)
2) 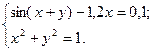
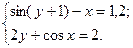 2)
2) 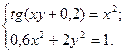
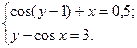 2)
2) 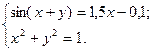
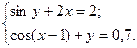 2)
2) 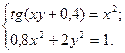
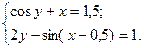 2)
2) 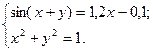
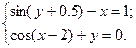 2)
2) 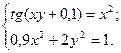
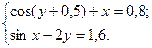 2)
2) 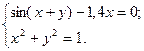
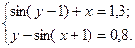 2)
2) 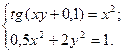
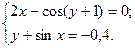 2)
2) 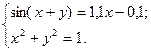
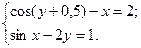 2)
2) 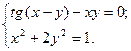
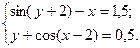 2)
2) 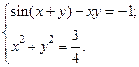
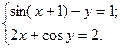 2)
2) 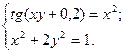
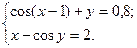 2)
2) 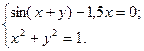
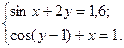 2)
2) 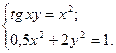
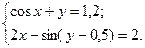 2)
2) 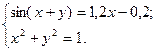
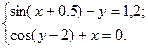 2)
2) 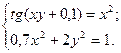
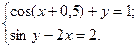 2)
2) 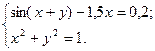
 2)
2) 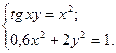
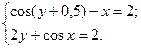 2)
2) 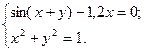
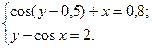 2)
2) 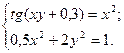
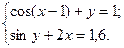 2)
2) 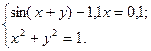
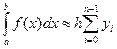 , (3.1)
, (3.1)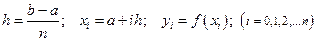
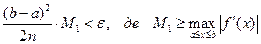 (3.2)
(3.2)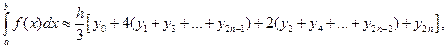 (3.3)
(3.3)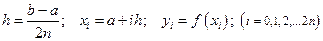
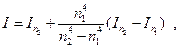 (3.4)
(3.4)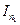 ,
, 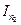 - два наближених значення
- два наближених значення 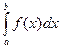 ,знайдених по формулі параболи для n1 та n2 (n2 > n1).
,знайдених по формулі параболи для n1 та n2 (n2 > n1).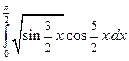 ; 2)
; 2)  .
.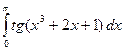 ; 2)
; 2) 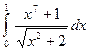 .
.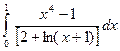 ; 2)
; 2) 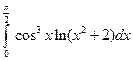 .
.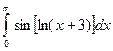 ; 2)
; 2) 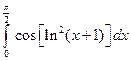 .
.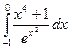 ; 2)
; 2) 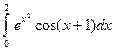 .
.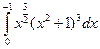 ; 2)
; 2) 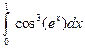 .
.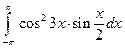 ; 2)
; 2) 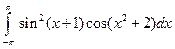 .
.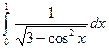 ; 2)
; 2) 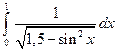 .
. ; 2)
; 2) 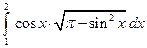 .
.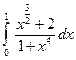 ; 2)
; 2) 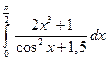 .
.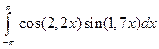 ; 2)
; 2) 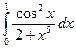 .
.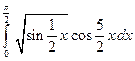 ; 2)
; 2) 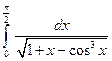 .
.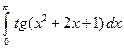 ; 2)
; 2) 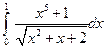 .
.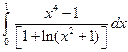 ; 2)
; 2) 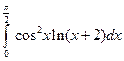 .
.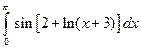 ; 2)
; 2) 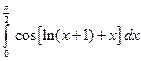 .
.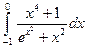 ; 2)
; 2) 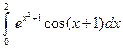 .
.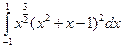 ; 2)
; 2) 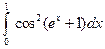 .
.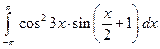 ; 2)
; 2) 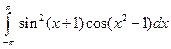 .
.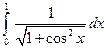 ; 2)
; 2) 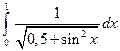 .
.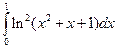 2)
2) 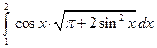 .
.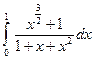 ; 2)
; 2) 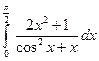 .
.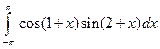 ; 2)
; 2) 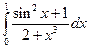 .
.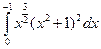 ; 2)
; 2) 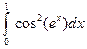 .
.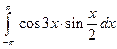 ; 2)
; 2) 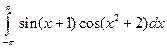 .
.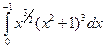 ; 2)
; 2) 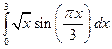 ; 2)
; 2) 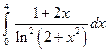 .
.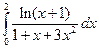 ; 2)
; 2) 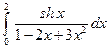 .
.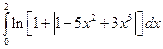 ; 2)
; 2) 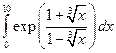 .
.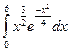 ; 2)
; 2) 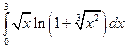 .
.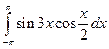 ; 2)
; 2)  .
.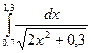 за формулою прямокутників з точністю ε=0,01.
за формулою прямокутників з точністю ε=0,01.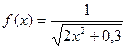 на проміжку [0,7;1,3].
на проміжку [0,7;1,3].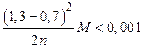 ,
,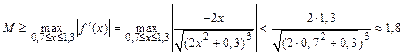 ,
,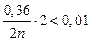 ;
; 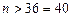 .
.

 0,406865.
0,406865.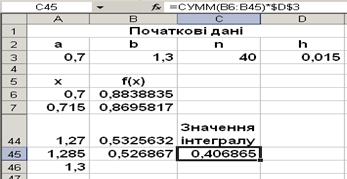
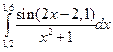 за формулою
за формулою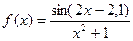 , оберемо n1 = 10, n2 = 15, які розмістимо на листі Excel з ім’ям „Сімпсона”. На цьому ж листі розмістимо кнопку Command Button1, як показано на рис. 3.3 та створимо процедуру рішення.
, оберемо n1 = 10, n2 = 15, які розмістимо на листі Excel з ім’ям „Сімпсона”. На цьому ж листі розмістимо кнопку Command Button1, як показано на рис. 3.3 та створимо процедуру рішення.



 (4.1)
(4.1) (4.2)
(4.2)



