ТЕМА: Наближення (інтерполяція) функцій

 

Теоретичні відомості

Задача наближення функції виникає, коли для функції, даної при дискретних значеннях аргументу у вигляді таблиці (ці значення називаються вузлами інтерполяції) необхідно знайти значення функції в проміжних крапках. Накладаючи вимогу, щоб наближена функція у вузлах співпадала з табличними значеннями (рис. 4.1), одержуємо задачу інтерполяції.

 

 

Рисунок 4.1 – Графік наближеної функції

 

Нехай в результаті спостережень за ходом деякого процесу побудована таблиця:

 

x	x0	x1	x2	…	xn
f(x)	f(x0)	f(x1)	f(x2)	…	f(xn)

 

Тобто, функція f(x) задана таблицею значень для кінцевої безлічі значень х.

Якщо необхідно знайти значення f(x) для проміжного значення аргументу, то будують функцію φ(x), просту для обчислень і таку, що для заданих x₀, x₁, x₂,..., x_n приймає значення f(x₀), f(x₁), f(x₂),..., f(x_n).

В інших точках відрізка [x_0, x_n] вважаємо, що φ(x) приблизно визначає функцію f(x) з тим чи іншим ступенем точності.

Найчастіше, функцію φ(x) представляють у вигляді алгебраїчного багаточлена деякого ступеня.

Найпростіша інтерполяція – це лінійна, тобто, коли невідому аналітичну залежність f(x) замінюють відрізками прямих, які проходять через відповідні вузли інтерполяції. В цьому випадку потрібно визначити якому відрізку належить надане х^* і за формулою лінійної інтерполяції знаходять f(x^*). Якщо x_i <= x^* <= x_i+1, то відповідна пряма проходить через вузли (x_i, f(x_і)), (x_i+1, f(x_і+1)):

(4.1)

 

Точність підрахунків в цьому випадку незначна, тому що враховується вплив тільки 2-ох вузлів інтерполяції. Частіше будують багаточлен P_n(x) ступеня n, що в (n+1) даних точках x₀, x₁, x₂,..., x_n. приймає дані значення y₀ = f(x₀), y₁ = f(x₁), …, y_n = f(x_n), тобто

f(x_і) = P_n(x_і), (і = 0, 1, 2,..., n).

Відзначимо, що двох різних інтерполяційних багаточленів одного і того же ступеня n існувати не може. Цим умовам задовольняє інтерполяційний багаточлен Лагранжа:

(4.2)

 

Тоді

 

Індивідуальні завдання

 

Для кожного варіанту обчислити наближене значення функції, яка задана таблицею, для наданого х^*, використовуючи лінійну інтерполяцію по Лагранжу.

 

4.2.1 х^* = 1,50

 

x	1,21	1,29	1,45	1,61	1,94	2,22
y	3,54	4,11	4,78	4,33	4,01	3,66

4.2.2 х^* = 0,45

 

x	0,24	0,39	0,65	0,88	0,94	1,12
y	2,18	1,98	1,73	1,13	1,01	1,34

 

4.2.3 х^* = 0,66

 

x	0,28	0,42	0,56	0,63	0,84	0,98
y	5,26	6,21	6,66	6,93	7,25	5,99

 

4.2.4 х^* = 3,2

 

x	2,10	2,19	2,35	2,51	2,82	3,33
y	8,54	8,11	7,78	7,03	6,77	7,86

 

4.2.5 х^* = 3,50

 

x	3,12	3,28	3,54	3,72	3,88	4,12
y	7,04	6,50	6,11	5,23	4,81	6,12

 

4.2.6 х^* = 0,85

 

x	0,25	0,54	0,65	0,80	0,94	1,12
y	0,54	0,91	1,78	2,33	2,81	3,66

 

4.2.7 х^* = 1,74

 

x	1,26	1,39	1,55	1,71	2,08	2,20
y	1,58	4,06	3,98	3,46	3,12	2,42

 

4.2.8 х^* = 4,51

 

x	4,02	4,38	4,44	4,58	4,74	4,98
y	10,54	4,82	4,93	5,14	5,92	7,12

 

4.2.9 х^* = 1,90

 

x	1,22	1,69	1,85	2,22	2,46	2,72
y	0,52	0,98	1,78	2,33	2,01	1,66

 

4.2.10 х^* = 3,82

 

x	3,41	3,59	3,75	3,89	4,00	4,18
y	4,50	4,19	3,81	4,33	3,66	2,84

 

4.2.11 х^* = 2,22

 

x	2,12	2,42	2,65	2,71	2,99	3,12
y	1,50	1,92	2,78	2,03	3,16	2,88

 

4.2.12 х^* = 5,32

 

x	5,13	5,29	5,45	5,61	5,84	6,22
y	1,54	1,11	1,78	1,33	1,01	2,66

 

4.2.13 х^* = 1,35

 

x	1,21	1,29	1,45	1,61	1,92	1,22
y	3,54	4,11	4,78	4,33	4,01	3,66

 

4.2.14 х^* = 0,80

 

x	0,22	0,42	0,63	0,78	0,82	0,99
y	6,52	6,88	7,55	6,15	7,92	8,02

 

4.2.15 х^* = 2,85

 

x	2,22	2,39	2,55	2,72	2,84	3,02
y	2,54	2,11	2,78	3,33	2,01	4,66

 

4.2.16 х^* = 0,60

 

x	0,28	0,49	0,65	0,71	0,96	1,22
y	3,54	4,11	4,78	4,33	4,01	3,66

 

4.2.17 х^* = 1,52

 

x	1,12	1,29	1,45	1,61	1,94	2,22
y	3,54	4,11	3,08	4,33	4,01	6,06

 

4.2.18 х^* = 3,50

 

x	3,12	3,29	3,45	3,66	3,84	4,02
y	3,54	2,11	1,78	1,33	2,01	0,54

 

4.2.19 х^* = 1,44

 

x	1,18	1,39	1,55	1,71	2,94	3,32
y	6,54	4,11	3,78	6,33	3,51	3,04

 

4.2.20 х^* = 0,56

 

x	0,12	0,31	0,45	0,61	0,98	1,32
y	2,54	3,22	3,58	3,13	4,01	4,26

 

4.2.21 х^* = 1,82

 

x	1,22	1,29	1,55	1,71	2,04	2,32
y	3,04	2,77	2,44	2,08	2,84	1,86

 

4.2.22 х^* = 2,50

 

x	2,32	2,49	2,65	2,81	3,04	3,18
y	3,54	4,11	4,78	4,33	4,01	5,66

 

4.2.23 х^* = 3,35

 

x	3,12	3,29	3,45	3,61	3,94	3,22
y	4,54	5,11	5,78	5,33	6,02	6,66

 

4.2.24 х^* = 1,50

 

x	1,32	1,29	1,44	1,66	1,98	2,26
y	3,54	3,11	2,78	2,33	4,01	2,16

 

4.2.25 х^* = 1,56

 

x	1,28	1,39	1,49	1,61	1,94	2,22
y	0,56	0,88	1,78	2,33	2,01	2,66

 

4.2.26 х^* = 1,08

 

x	0,07	1,29	1,45	1,61	1,94	2,22
y	3,54	4,11	4,78	4,33	4,22	3,66

 

4.2.27 х^* = 3,33

 

x	3,12	3,39	3,48	3,61	3,94	3,22
y	3,54	3,11	2,78	2,33	4,01	2,16

 

4.2.28 х^* = 1,44

 

x	0,88	1,26	1,35	1,58	1,74	1,98
y	2,46	2,71	2,98	3,33	3,00	3,37

 

4.2.29 х^* = 1,50

 

x	1,42	1,59	1,65	1,71	1,94	2,22
y	5,12	4,12	3,76	3,50	4,01	2,83

 

4.2.30 х^* = 1,74

 

x	1,12	1,29	1,45	1,61	1,94	2,22
y	2,54	2,11	2,78	2,33	2,01	2,66

 

Приклади виконання лабораторної роботи

 

Приклад 4.3.1 Обчислити наближене значення функції, заданої у вигляді таблиці для х^*=0,702, використовуючи лінійну інтерполяцію.

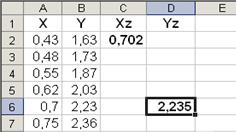
Вирішимо задачу у середовищі Excel. На листі з ім’ям “Лін_інтерполяція” розмістимо надану таблицю значень, як показано на рис. 4.1.

 

 

Рисунок 4.1 – Зразок листа Excel “Лін_інтерполяція”

 

Для цього до клітини D2 введемо формулу (4.1):

 

= ЕСЛИ(И($С$2>=A2;$C$2<=A3);B2+($C$2–A2)*(B3–B2)/(A3-A2):“”)

 

Використовуючи маркер заповнювання, копіюємо формулу до клітини С3:С6. Якщо х^* є [ x₀, x_n], то відповідне y^* буде підраховане, як показано на рис. 4.2.

Якщо x^* не належить [ x₀, x_n] будемо мати пустий стовпчик С, тобто лінійну інтерполяцію в цьому випадку не можна використовувати.

Протокол рішення зображено на рис. 4.2.

 

 

Рисунок 4.2 – Протокол рішення

 

Приклад 4.3.2 Обчислити наближене значення функції, заданої у вигляді таблиці для х^*=0,702, використовуючи інтерполяцію по Лагранжу.

Як і у попередньому прикладі, можна розмістити початкові дані, тобто значення х^*, та таблицю значень на листі Excel з ім’ям „Лагранжа”, як показано на рис. 4.3.

 

 

Рисунок 4.3 – Зразок листа Excel „Лагранжа”

 

Помістимо об’єкт – „командна кнопка” з ім’ям CommandButton1, змінимо відповідні властивості Caption, Font. Зв’яжемо з подією Click на кнопці процедуру побудови інтерполяційного багаточлена Лагранжа, та підрахунку значення функції для заданого х^*=0,7.

 

 

Текст процедури:

 

Протокол рішення зображено на рис. 4.4.

 

 

Рисунок 4.4 – Протокол рішення прикладу

ЛАБОРАТОРНА РОБОТА №5

 

ТЕМА: Апроксимація даних (емпіричні формули)

 

Теоретичні відомості

Нерідко при обробці результатів спостережень зустрічаються з наступною задачею: у підсумку досвіду отриманий ряд значень змінних х і у, однак характер функціональної залежності між ними залишається невідомим, потрібно по отриманим даним знайти аналітичне вираження між x і y. Формули, отримані в результаті рішення подібного роду задач, називаються емпіричними.