Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методичні вказівки до виконання индивідуального завданняСодержание книги
Поиск на нашем сайте
Загальні вимоги
Індивідуальне завдання передбачає відповіді на два теоретичних питання та рішення чотирьох задач. Варіант індивідуального завдання відповідає останнім двом цифрам залікової книжки, які визначають учбовий шифр студента. Номери теоретичних питань, зміст яких наведений у розділі 3, та номери задач студент вибирає за своїм варіантом з п. 6.2. Варіант вихідних даних для розв/язання задач вибирають з відповідних таблиць до них за останньою цифрою шифру. Наприклад, за варіантом індивідуального завдання 57 студент повинен відповісти на питання № 32 «Визначення кількості повторних дослідів» та № 10 «Фізичні та математичні моделі випадкового процесу, реактора ідеального змішування», а також вирішити задачі №№ 7, 11, 15, 19 за варіантом вихідних даних до них № 7. До структури індивідуального завдання входить титульний аркуш та зміст; відповіді на теоретичні питання; рішення задач; перелік використаної літератури, інших джерел інформації. На титульному аркуші слід обов’язково вказати учбовий шифр виконавця; у разі його відсутності завдання повертається рецензентом без перевірки. Індивідуальне завдання виконують, як правило, у надрукованому вигляді на аркушах формату А-4, пронумерованих і скріплених належним чином. Можливо також виконання завдання у рукописному вигляді, чітким і розбірливим почерком в учнівському зошиті або на аркушах формату А-4. На кожній сторінці залишають поля для зауважень рецензента. При складанні кожної відповіді слід спочатку навести № та зміст теоретичного питання; відповіді на питання повинні бути чіткими, повними, з посиланням на джерела інформації. До кожної задачі треба вказати її № та умови, № варіанту та значення вихідних даних; детальний розрахунок зі всіма необхідними коментарями, ілюстраціями, формулами. Кожна задача повинна містити висновок щодо результатів рішення. У кінці індивідуального завдання, після переліку використаної літератури, слід поставити дату виконання та підпис. Студент подає індивідуальне завдання на перевірку у заплановані графіком навчального процесу строкі і після врахування зауважень і оформлення здійснюється захист роботи. Зараховане індивідуальне завдання подається викладачеві під час складання підсумкового контролю.
Варіанти індивідуальних завдань
Задачи для виконання індивідуального завдання та методичні вказівки до їх рішення Задача 1 Вміст речовини С в реакторі ідеального змішування об/ємом V у часі τ змінюється за рівнянням
Таблиця 1 Вихідні дані до задачі 1.
Вказівки до рішення. За цим рівнянням швидкість зміни концентрації речовини в апараті і на його виході пропорційна різниці між вхідною і вихідною концентрацією. При ступінчастому зміненні вхідної концентрації з С0 до Свх маємо:
Після інтегрування та потенціювання отримуємо:
де А – стала інтегрування, яку знаходять з початкових умов (при τ = 0; С = С0):
Тоді можемо отримати рівняння динаміки концентрації речовини у реакторі:
З іншого боку маємо:
Звідсі можна визначити час τ = τ2 для досягнення концентрації речовини у реакторі С = С2. Для побудови залежності С = f(τ), окрім початкової точки (τ = 0; С = С0) та вже визначених (τ = τ1; С = С1 та τ = τ2; С = С2), достатньо визначити С ще в двох – трьох точках, наприклад, при
Задача 2
Маса нерозчиненої речовини m у часі τ змінюється за рівнянням
Таблиця 2 Вихідні дані до задачі 2.
Вказівки до рішення. За наведеним диференційним рівнянням швидкість розчинення є пропорційною кількості нерозчиненої речовини і з часом процес розчинення згасає. В цьому можна переконатися з його рішення:
Сталу інтегрування С2 знаходимо з початкових умов: при τ=0 початкова кількість нерозчиненої речовини m=m0. Тоді маємо:
m0=
і кінцево отримуємо: m = m0e-К·
Значення часу для досягнення деякої заданої величини m отримують шляхом логарифмування цього рівняння. Для побудови графіку m = f(τ) можна використати початкову точку (τ = 0; m = m0), дві вже визначені (τ = τ1; m = m1 та τ = τ2; m = m2) та ще дві – три точки, наприклад, при
Задача 3 Знайти температуру t тіла, що змінюється за рівнянням
Таблиця 3 Вихідні дані до задачі 3.
Вказівки до рішення. Наведене диференційне рівняння першого порядку можна записати наступним чином:
Зважаючи на те, що tср = соnst, перетворимо отримане рівняння, проінтегруємо його та виконаємо потенціюнування отриманого рішення:
Визначимо з початкових умов сталу інтегрування С2: - при τ = 0; Таким чином, маємо:
З передостаннього виразу можна визначити температуру тіла t1 у будь-який момент часу τ1, а шляхом логарифмування останнього виразу можна знайти час τ2 досягнення заданої температури тіла t2. Для побудови графіку t = f(τ) можна використати початкову точку (τ = 0; t = t0), дві вже визначені (τ = τ1; t = t1 та τ = τ2; t = t2) та ще дві – три точки, наприклад, при Всі розрахунки слід виконувати у системі СІ.
Задача 4 Вміст пилу в газі Z під час руху τ в пластинчастому електрофільтрі змінюється за рівнянням
Таблиця 4 Вихідні дані до задачі 4.
Вказівки до рішення. Шляхом розділення змінних та інтегрування вихідного диференційного рівняння отримуємо:
Сталу інтегрування знаходимо з початкових умов (при τ = 0; Z = Z0):
Тобто, вміст пилу в газі при русі у пластинчастому електрофільтрі знижується за виразом:
Відношення фактичного вмісту пилу у газі до початкового на вході в електрофільтр у будь-який момент часу становить Для побудови графіку Z = f(τ) можна використати початкову точку (τ = 0; Z= Z0), дві вже визначені (τ = τ1; Z = Z1 та τ = τ2; Z = Z2) та ще дві – три точки, наприклад, при
Задача 5 Вміст пилу в газі Z під час руху τ в трубчастому електрофільтрі змінюється за рівнянням
Таблиця 5 Вихідні дані до задачі 5.
Вказівки до рішення. При рішенні задачі 5 можна керуватися методичними вказівками до задачі 4, де замість відношення
Задача 6 За рівнянням кінетики крекінгу нафтової сировини
Таблиця 6 Вихідні дані до задачі 6.
Вказівки до рішення. З вихідного рівняння шляхом розділення змінних та інтегрування отримуємо:
З початкових умов (при τ = 0; х = х0) отримуємо сталу інтегрування:
Тоді кінцеве рішення буде мати вигляд:
звідки можна знайти залежність х = f(τ). Отримати вираз для визначення величини τ2, коли буде досягнута значення х = х2, можна шляхом логарифмування відношення:
Для побудови графіку х = f(τ) можна використати початкову точку (τ = 0; х = х 0), дві вже визначені (τ = τ1; х = х 1 та τ = τ2; х = х 2) та ще дві – три точки, наприклад, при
Задача 7
Визначити показники ступенів х, у, z в безрозмірному комплексі, вказаному в табл. 7, де F – сила, μ – коефіцієнт динамічної в/язкості, а – прискорення, Р – тиск, ω – швидкость руху, ρ – густина речовини, S – площа.
Таблиця 7 Вихідні дані до задачі 7.
Вказівки до рішення. Розмірності наведених в умовах задачі параметрів:
Отримання безрозмірного комплексу [F] = [μx а y Pz ]; Складемо рівняння показників ступеню за основними розмірностями: - (кг) 1 = x + z; - (м) 1= - х + у – z; - (с) - 2 = - х – 2y – 2z. Зі спільного рішення ціх рівнянь отримуемо: х = 4; у = 2; z = - 3. Таким чином, безрозмірний комплекс має вигляд Задача 8
Визначити показники ступенів х, у, z в безрозмірному комплексі, вказаному в табл., де d – характерний розмір, а – коефіцієнт температуропровідності, g – прискорення вільного падіння, Р – тиск, ω – швидкость руху, ρ – густина речовини, Q – питома теплота згоряння газового палива, q - густина теплового потоку, μ – коефіцієнт динамічної в/язкості.
Таблиця 8 Вихідні дані до задачі 8.
Вказівки до рішення. Розмірності Р, ω, ρ та μ наведені у методичних вказівках до попередньої задачі; розмірності інших параметрів становлять:
Значення показників ступеню х, у та z для параметрів у знаменнику заданих безрозмірних комплексів знаходять з системи рівнянь, складених відносно основних одиниць виміру (м, с, кг), як це розтлумачено у вказівках до рішення задачі 7. Задача 9 За залежністю
Таблиця 9 Вихідні дані до задачі 9.
Вказівки до рішення. Необхідною умовою наявності екстремуму цільової функції
Характер екстремуму цільової функції в стаціонарній точці визначає значення її другої похідної: ознакою досягнення мінімуму є її позитивність, тобто:
Тому знайдемо першу та другі похідні цільової функції
Таким чином, прирівнюємо першу похідну нулю, звідки знаходимо значення Р*; підставляємо Р* у вираз для другої похідної цільової функції та переконуємося, що дійсно у цій точці має місце мінімум; розраховуємо значення цільової функції при Р = Р*. Для побудови графіку m = f(P), окрім оптимальної точки, слід визначити значення цільової фукції ще у двох-трьох точках при Р < P* (наприклад, при Р = 0,25P*; Р = 0,5P*; Р = 0,75P*) та при Р > P* (наприклад, при Р = 1,25P*; Р = 1,5P*; Р = 2P*).
Задача 10 За залежністю Таблиця 10 Вихідні дані до задачі 10.
Вказівки до рішення. При рішенні цієї задачі слід керуватися вказівками до задачі 9 з урахуванням, що ознакою досягнення максимуму цільової функції є негативність її другої похідної при Р = Р*, тобто:
Перша та друга похідні цільової функції
Задача 11 Знайти швидкість руху газу ω, м/с, через очисний апарат, що забезпечує мінімум вмісту пилу на його виході Z, мг/м3, якщо залежність між ними Таблиця 11 Вихідні дані до задачі 11.
Вказівки до рішення. При рішенні цієї задачі слід керуватися вказівками до задачі 9.Перша та друга похідні цільової функції
Задача 12 Знайти швидкість руху газу ω, м/с, через очисний апарат, що забезпечує мінімум вмісту пилу на його виході Z, мг/м3, якщо залежність між ними Таблиця 12 Вихідні дані до задачі 12.
Вказівки до рішення. При рішенні цієї задачі слід керуватися вказівками до задачі 9. Перша та друга похідні цільової функції
Задача 13
Знайти оцінку математичного очікування та дисперсії концентрації SO2 у газових викидах агрегату, а також їх довірчі інтервали за даними, що наведені у табл. 13, для рівня значимості q = 5%.
Таблиця 13 Вихідні дані до задачі 13.
Вказівки до рішення. Оцінки математичного очікування та дисперсії для дискретної випадкової величини визначаються за формулами:
де N – кількість вимірів. Розрахунок інтервальних оцінок для математичного очікування
де f = N – 1 - числом ступенів свободи вибірки; Sх – середньоквадратичне відхилення; tq – значення критерію Стьюдента, який знаходять з додатку Б для f = N – 1 і заданого рівня значимості q = 5%;
Задача 14
Чи суттєво відрізняється від середньорічного значення х 0 середній вміст NOx у газових викидах з агрегату
Таблиця 14 Вихідні дані до задачі 14.
Вказівки до |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 196; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.29.248 (0.012 с.) |
. Знайти С при τ = τ1, якщо в реактор надходить потік з об/ємною витратою v та вмістом речовини Свх, а при τ = 0 С = С0. Через який час величина С буде дорівнювати С2? Побудуйте графік зміни концентрації речовини у часі.
; 
.
; 
,
.
; 
.
; 
.
= 
; 
; 
.
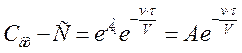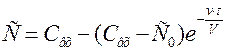. Якою буде величина m при τ = τ1, якщо при τ = 0 m = m0? Який час потрібний, щоб залишилося m = m2 нерозчиненої речовини? Побудуйте графік зміни кількості нерозчиненої речовини у часі.
; ln m = - k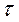 
+ С1; m = е-К· 
+С1 = С2 ·е- К·τ
C2 = m0
.
; 
; 
.
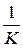, через час τ = τ1, хвилин, якщо при τ = 0 t = t0, 0С. Теплоємність тіла С, Дж/(кг·К); його густина ρ, кг/м3; об/єм V, м3; площа поверхні F, м2; густина теплового потока q = α(tср-t), Вт/м2; коефіцієнт тепловіддачи α, Вт/(м2·К); температура середовища tср, 0С. За який час температура досягне t = t2,0С? Побудуйте графік зміни температури тіла у часі.
; 
.
; 
;
.
.
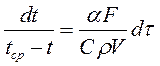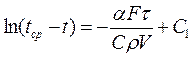або 
.
; 
; 
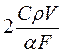або інші.
. Знайти вміст пилу в газі через τ = τ1, с, якщо швидкість дрейфу частинок пилу ωд, см/с; відстань між електродами с,мм; при τ = 0 Z = Z0, мг/м3. Через який час перебування у електрофільтрі вміст пилу в газі буде Z2, мг/м3? Побудуйте графік зміни вмісту пилу в газі у часі.
; 
; 
.
.
.
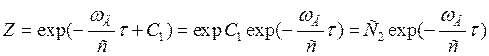, звідки шляхом логарифмування можна знайти час τ2 досягнення вмісту пилу Z2.
; 
; 
або інші. Всі розрахунки слід виконувати у системі СІ.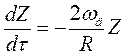
. Знайти вміст пилу в газі через τ = τ1, с, якщо швидкість дрейфу частинок пилу ωд, см/с; радіус осаджувального електрода R, мм; при τ = 0 Z = Z0, мг/м3. Через який час вміст пилу в газі буде Z2, мг/м3? Побудуйте графік зміни вмісту пилу в газі під час перебування у електрофільтрі.
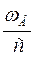буде фігурувати 
.
визначити кількість перетвореної сировини х до часу τ = τ1, с, якщо константа швидкості реакції k, с-1; на момент τ = 0 з а, кг вихідної сировини перетворено х = х0, кг. Знайти час τ2, коли маса перетвореної сировини х буде складати х2, кг. Побудуйте графік залежності х = f(τ).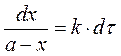
; 
; 
; 
.
.
,
.
; 
; 
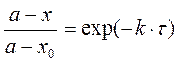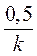або інші.
; 
;
; 
; 
;
; 
.
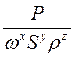
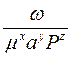
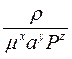
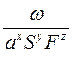
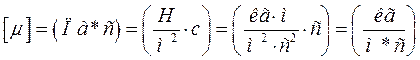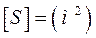, де α, α1, α2, α3 – деякі параметри, можливо, якщо розмірність чисельника дорівнює розмірністі знаменника. Для цього показник ступеня у чисельнику за кожної основної одиниці виміру (м, с, кг і т.д.) повинен дорівнювати сумі показників ступеню цієї одиниці у знаменнику. Тобто, значення показників ступеню х, у та z для окремих параметрів α1, α2, α3 можна знайти з системи рівнянь, складених відносно основних одиниць виміру (м, с, кг). Наприклад, для комплексу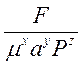 
можна записати:
.
.
; 
; 
; 
; 
.
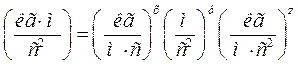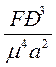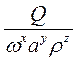
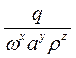
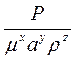
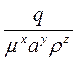
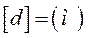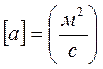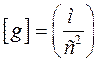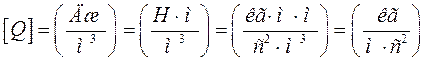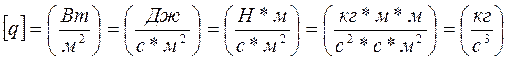визначити оптимальну продуктивність агрегату Р*, що забезпечує мінімальні питомі викиди шкідливих речовин 
, та величину 
. Побудуйте графік залежності питомих викидів шкідливих речови х від продуктивності агрегату.
при деякому значенні продуктивності агрегату Р* є рівність нулю її першої похідної за цим параметром:
.
.
:
;
.
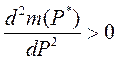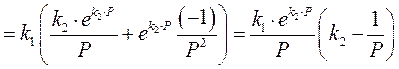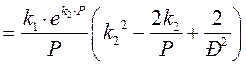визначити оптимальну продуктивність агрегату Р*, що забезпечує максимальний ККД агрегату 
, та величину 
. Побудуйте графік залежності ККД від продуктивності агрегату.
.
становлять:
;
.
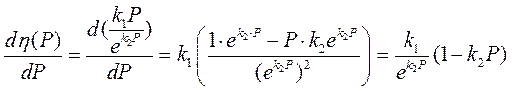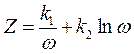. Яким буде цей мінімальний вміст пилу після очищення? Побудуйте графік залежності Z = f(ω).
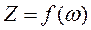становлять:
;
.
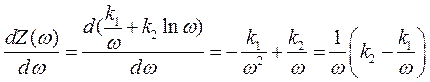. Яким буде цей мінімальний вміст пилу після очищення? Побудуйте графік залежності Z = f(ω).
; 
.
; 
.
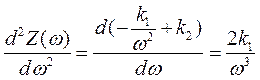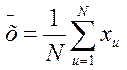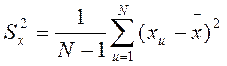та дисперсії 
деякої змінної Х виконується за формулами: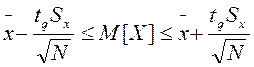
; 
,
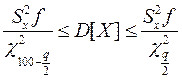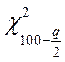та 
- значення χ2 – розподілу Пірсона для для f = N – 1 і рівня значимості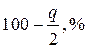 
та 
відповідно, що знаходять з додатку В.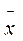
, що визначений за серією вимірів (табл. 14) для рівня значимості q = 5%?
