
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Регресійні залежності довільного типуСодержание книги
Поиск на нашем сайте
Тут треба написати про нелінійні регресії (наприклад, поліноміальні), про цікаві функції (наприклад, функції Кобба-Дугласа), про використання моделей з різними змінними (якісними та кількісними - фіктивні змінні). Це таке Фіктивні змінні. У попередніх розділах ми розглядали змінні, які можна вимірювати за допомогою кількісних шкал (вартість капіталу, рівень інфляції, обсяг попиту і т.ін.). Однак, у багатьох випадках на поведінку змінної, яку ми вивчаємо впливають якісні фактори, наприклад, наявність або відсутність вищої освіти, статеві, расові відмінності. Для врахування дії подібних чинників застосовують фіктивні змінні. Фіктивні, або бінарні змінні можуть приймати два значення: 0 та 1. Розглянемо декілька прикладів. Нехай ми вивчаємо залежність заробітної платні від віку та рівня освіти за допомогою такої моделі
де y – величина зарплатні, x1 – вік у роках, x2 – рівень освіти, який вимірюється у роках навчання. Припустимо, що нам потрібно виявити, чи існує відмінність в оплаті праці між чоловіками і жінками. Для цього ми утворюємо фіктивну змінну D: D = 1 для чоловіків і D = 0 для жінок. Модель набуде вигляду
Величина коефіціента b3 показує відмінність у седньому рівні заробітної платні між чоловіками і жінками, які мають однаковий вік та рівень освіти. Для того, щоб відтворити в моделі вплив якісного фактора, який може приймати m рівнів, в модель потрібно включити m –1 фіктивну змінну. Нелінійна регресія Якщо графік регресії Обернена функція має вигляд: тобто узагальнені регресії моделі відповідно будуть: а вибіркові нелінійні регресії є:
За методом найменших квадратів параметри
Для аналізу зв’язку y і х в цих випадках використовуються кореляційними відношеннями:
де Модель Коба-Дугласа та її оцінка Розглянемо виробничу функцію Коба–Дугласа: Y = AL a C b, (1.59) де Y –валовий випуск, L– обсяг трудових ресурсів, С –обсяг капіталу (виробничих фондів), A, a, b – параметри. Коефіцієнт пропорційності A відображає рівень технології. Парамери a та b є коефіцієнтами еластичності відносно праці та капіталу (отже, функція Коба–Дугласа є виробничою функцією зі сталою еластичністю). Прологарифмувавши рівняння (1.59), маємо: y = a + a l + b c, (1.60) де a = ln A, l = ln L, c = ln C. Якщо ввести до рівняння (1.60) стохастичний доданок, то одержимо модель лінійної регресії: y = a + a l + b c +e. (1.61) Щоб перетворити вихідну модель (1.59) на стохастичну, обчислимо експоненту від обох частин рівності (1.61): Y = AL a C bee. (1.62) Ми бачимо, що модель (1.62) можна звести до моделі лінійної регресіі. Аналогічно можна вивчати досить широкий клас моделей, які за допомогою перетворень змінних та рівнянь можна звести до моделі лінійної регресії. Широковживаним є приклад поліноміальної регресії:
Модель Коба-Дугласа та її оцінка Розглянемо виробничу функцію Коба–Дугласа: Y = AL a C b, (1.59) де Y –валовий випуск, L– обсяг трудових ресурсів, С –обсяг капіталу (виробничих фондів), A, a, b – параметри. Коефіцієнт пропорційності A відображає рівень технології. Парамери a та b є коефіцієнтами еластичності відносно праці та капіталу (отже, функція Коба–Дугласа є виробничою функцією зі сталою еластичністю). Прологарифмувавши рівняння (1.59), маємо: y = a + a l + b c, (1.60) де a = ln A, l = ln L, c = ln C. Якщо ввести до рівняння (1.60) стохастичний доданок, то одержимо модель лінійної регресії: y = a + a l + b c +e. (1.61) Щоб перетворити вихідну модель (1.59) на стохастичну, обчислимо експоненту від обох частин рівності (1.61): Y = AL a C bee. (1.62) Ми бачимо, що модель (1.62) можна звести до моделі лінійної регресіі. Аналогічно можна вивчати досить широкий клас моделей, які за допомогою перетворень змінних та рівнянь можна звести до моделі лінійної регресії. Широковживаним є приклад поліноміальної регресії:
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 342; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.24.110 (0.007 с.) |

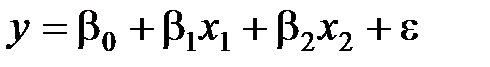 ,
,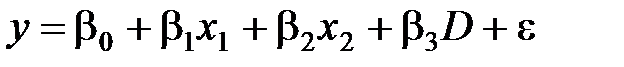 .
.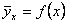 або
або 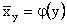 зображується кривою лінією, то кореляцію називають криволінійною (нелінійною). Наприклад, квадратичні функції використовуються для опису дуже широкого спектру економічних процесів, завдяки їхнім універсальним властивостям. Дійсно, у загальному випадку квадратична функція має вигляд:
зображується кривою лінією, то кореляцію називають криволінійною (нелінійною). Наприклад, квадратичні функції використовуються для опису дуже широкого спектру економічних процесів, завдяки їхнім універсальним властивостям. Дійсно, у загальному випадку квадратична функція має вигляд: 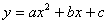 . (1)
. (1)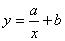 , (2)
, (2)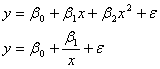 , (3)
, (3)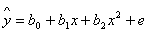 (4)
(4)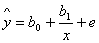 (5)
(5)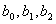 знаходять з системи:
знаходять з системи: , (6)
, (6) (7)
(7) , (8)
, (8)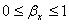 .
.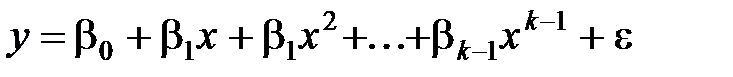 .
.


