Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення економетрії як науки, її природа. Приклади використання економетричних моделей для розв’язування економічних задач.Содержание книги
Поиск на нашем сайте
Визначення економетрії як науки, її природа. Приклади використання економетричних моделей для розв’язування економічних задач. Економетрика – наука, що вивчає економічні моделі та процеси за допомогою математичних та статистичних методів.-конспект Економетрика (за підр. Черняка) – наука, що вивчає кількісні взаємозв’язки економічних об’єктів і процесів за допомогою математичних і статистичних методів і моделей. Економетричні методи передбачають статистичний аналіз конкретних економічних даних зазвичай за допомогою комп’ютерів. Також, можна описати економетрику, як галузь економічної теорії, яка вивчає моделі економічних систем у такій формі, яка дає можливість перевіряти ці моделі на адекватність засобами математичної статистики. Основна задача економетрики полягає в практичній перевірці основних економічних концепцій та положень.-конспект Економетрика – наука, яка вивчає конкретні кількісні та якісні взаємозв’язки економічних процесів за допомогою математичних та статистичних методів та моделей. Мета економетрики – здійснювати емпіричну перевірку положень економічної теорії, підтверджуючи чи відхиляючи останні. Цим економетрика відрізняється від математичної економіки, зміст якої полягає виключно у застосуванні математики, і теоретичні положення якої не обов’язково потребують емпіричного підтвердження. Економетрика є результатом синтезу економічної теорії, математичної статистики та економічної статистики. Застосування статистичних методів до аналізу економічних даних має давню історію. Перша «емпірична» крива попиту була опублікована Чарльзом Дейвенентом у 1699 році. Економічна модель являє собою набір припущень, які приблизно описують поведінку економіки (або сектора економіки). Економетрична модель складається з таких частин: 1). Набір рівнянь поведінки, які виводяться з економічної моделі. Ці рівняння включають деякі змінні, значення яких спостерігаються, а також «збурення», які відтворюють ефект від змінних, не включених до моделі у явному вигляді, та ефект від непередбачуваних подій. 2). Опис імовірнісного розподілу «збурень». Економетричні моделі мають стохастичний характер. Розглянемо співвідношення між споживанням С та доходом Y у такому вигляді: С = α + β Y + ε, де ε – збурення, або стохастична складова моделі, α і β – невідомі параметри, які можна оцінити за допомогою методів математичної статистики. Стохастичний характер економетричних моделей дозволяє використовувати теорію статистичних висновків для перевірки цих моделей на адекватність. Перевірка складається з двох етапів: статистичного і економічного. На статистичному етапі ми перевіряємо, чи виконуються вимоги, які накладено на стохастичну складову ε при формулюванні моделі. На економічному етапі ми перевіряємо, чи узгоджуються знайдені оцінки параметрів з положеннями економічної теорії. Наприклад, теорія споживання стерджує, що зі зростанням доходу споживання зростає, але не в такій мірі як доход. Звідси випливає, що ця модель коректна, при 0 < β < 1. Таким чином, економетричні методи дозволяють не тільки встановлювати кількісні зв’язки між економічними змінними, але й робити висновки про коректність одержаних моделей.
2. Роль економетричних досліджень в економіці. Роль економетричного дослідження визначається тими задачами, які може розв’язувати економетрія. Найважливішою задачею є оцінювання параметрів і перевірка значущості економетричної моделі. Етапи економетричного дослідження: 1) Формування економічної концепції чи гіпотези 2) Збір упорядкованої інформації та необхідних даних 3) Розрахунок моделі та перевірка її адекватності 4) Аналіз моделі, розробка прогнозів, перевірка економетричних тестів Структуру економетричних досліджень:
В сучасних умовах роль економетричних досліджень є значною. Відбувається розробка нових методів оцінювання параметрів моделей з урахуванням особливостей вихідної економічної інформації, а також розширення економічних досліджень на основі економетричних методів. Пояснення та аналіз актуальних економічних процесів та проблем невід’ємно пов’язано із використанням математичних методів. Саме вони забезпечують найбільш чітку та повну характеристику стану економіки й допомагають прийняти необхідні рішення для підвищення ефективності функціонування господарства країни.
МНК Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки. Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений. Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов Пусть надо решить систему уравнений (1)
Чтобы решить их по способу наименьших квадратов, составляют новую систему уравнений, число которых равно числу неизвестных и которые затем решаются по обыкновенным правилам алгебры. Эти новые, или так называемые нормальные уравнения составляются по следующему правилу: умножают сперва все данные уравнения на коэффициенты у первой неизвестной x и, сложив почленно, получают первое нормальное уравнение, умножают все данные уравнения на коэффициенты у второй неизвестной y и, сложив почленно, получают второе нормальное уравнение и т. д.
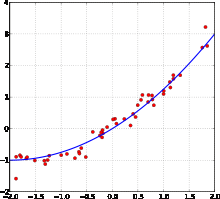
Пример кривой, проведённой через точки, имеющие нормально распределённое отклонение от истинного значения. то нормальные уравнения представятся в следующем простом виде: (2)
11. Властивості статистичних оцінок параметрів, їх характеристика. При оцінюванні бажано, щоб втрата інформації, яка може бути суттєвою для прийняття статистичних рішень, була мінімальною. Отже, для того, щоб оцінки були надійними, вони мають відповідати деяким вимогам, тобто володіти певними властивостями. Основними властивостями статистичних оцінок є спроможність, незмі-щенність, ефективність: o Спроможність. Статистична оцінка ®n спроможна тоді, коли при постійному збільшенні обсягу вибірки (n -"со) вона наближається до значення параметра ©, який оцінює. Статистика ©" є спроможною оцінкою параметpa 0, коли для будь-якого додатного числа є є справедливим співвідношення limP{©n -0>є = 0. (4.2) Наприклад, вибіркове середнє X є спроможною оцінкою генерального середнього fi, оскільки при збільшені числа випробувань X наближається до свого математичного сподівання (див. вираз (3.45)). Спроможною оцінкою вважається і вибіркова дисперсія. Вимога спроможності означає, що оцінка має нести практичний сенс, наближати нас до істини і не бути абсурдною. З другого боку, у більшості ситуацій можна запропонувати декілька спроможних оцінок для одного й того ж самого параметра. Отже, властивість спроможності необхідна, але недостатня вимога. її необхідно доповнити іншими вимогами. o Незміщенність. Статистика вважається незміщеною, якщо її математичне сподівання дорівнює параметру, що оцінюється. Вибіркове середнє X є незміщеною оцінкою генерального середнього fi, оскільки м[ X ] =ц, чого не можна сказати, наприклад, про вибіркові показники дисперсії. Для математичного сподівання можна записати
o Ефективність. Точкова оцінка називається ефективною, якщо вона має найменшу міру дисперсії вибіркового розподілу у порівнянні з аналогічними оцінками, тобто виявляє найменшу випадкову варіативність. Наприклад, серед трьох показників положення центру нормального розподілу (середнього Х, медіани ма і моди Мо) найбільш ефективною оцінкою вважається Х і найменш ефективною - Мо, оскільки для їхніх дисперсій характер- Для статистичного оцінювання параметрів генеральної сукупності бажано використовувати оцінки, які задовольняють одночасно вимоги спроможності, незміщенності й ефективності. Крім того, важливо знати, за якими методами відбувається вибір і побудова тієї чи іншої моделі статистичного оцінювання. Коефіцієнт детермінації.
Для обчислення коефіціента детермінації можна скористуватись ще такими формулами
Коефіціент детермінації є частиною дисперсії залежної змінної, яка пояснюється за рахунок моделі, або, іншими словами, завдяки мінливості незалежної змінної. Коефіціент детермінації є мірою тісноти саме лінійного зв¢язку між x та y. Коефіціент детермінації завжди знаходиться в межах від нуля до одиниці. Чим ближче
Рис 1.2. У випадку, зображеному на Рис. 1.2.а) має місце досить тісний лінійний зв’язок між змінними. У випадках б) та в) лінійний зв’язок практично відсутній. Однак між цими двома ситуаціями існує істотна різниця. На Рис. 1.2 б), очевидно, відсутній будь-який зв’язок між змінними, тоді як точки на Рис. 1.2.в) розташовані навколо деякої параболи.
Моделі, які зводяться до моделі простої (множинної МНЕ КАЖЕТСЯ ТУТ ОПЕЧАТКА) лінійної регресії. Приклади застосування простої лінійної регресії. Багато економічних процесів найкраще описувати нелінійними співвідношеннями. Проте дуже часто існує можливість за допомогою різноманітних математичних операцій звести такі функції до лінійних, які елементарно оцінити за допомогою моделі простої лінійної регресії. Нехай, досліджувана модель має такий вигляд:
Щоб привести цю модель до простої лінійної регресії, слід зробити такі зміни: 1. Логарифмувати обидві частини рівняння:
2. Позначити отримані величини:
3. Записати рівняння простої лінійної регресії:
Основні види перетворень для зведення моделей до простої лінійної регресії наведено в таблиці.
Слід зазначити, що не всі моделі можна звести до простої лінійної регресії, наприклад:
У цій моделі неможливо однозначно визначити окремо коефіцієнти Виділення сезонних коливань Ряд значень, взятих за певний часовий період, називається часовим рядом. Для того, щоб оцінити поведінку таких рядів, доцільно розділити ці значення на декілька складових. Ці складові можна розглядати як: тренд, циклічні, сезонні та випадкові коливання. Сезонні коливання — демонструють періодичність коливань протягом року (наприклад, обсяг продажу в зимові місяці вищий, в літні місяці він знижується, а восени знову починає зростати). Сезонні коливання можна вичленувати після аналізу тренду і циклічних коливань. Для визнач сезонних коливань будуємо модель виду:
де 1 q – фіктивна змінна, що приймає значення 1, якщо розглядається перший квартал року, 0 – в інших випадках, 2 q – фіктивна змінна, що приймає значення 1, якщо розглядається другий квартал року, 0 – в інших випадках, 3 q – фіктивна змінна, що приймає значення 1, якщо розглядається третій квартал року, 0 – в інших випадках, t – трендовий компонент, що показує зростання прибутків протягом часу спостережень.
Основні визначення Вид моделі. в якій вектор збурень не задовольняє класичним властивостям збурень: 1. Mv i = 0 2. Гетероскедастичність збурень: 3. Незалежність збурень: 4. Незалежність збурень та регресорів: 5. Збурення v i нормально розподілені для всіх i. Наслідки гетероскедастичності збурень на оцінки методу найменших квадратів: 1.Оцiнки МНК будуть незміщеними, але не будуть ефективними (не матимуть найменшої дисперсії). 2.Стандартнi оцінки коварiацiйної матриці оцінки МНК будуть зміщеними, i, як наслідок, процедури перевірки гіпотез та інтервального оцінювання, основані на стандартних статистиках, будуть некоректними. Критерій Голдфелда-Квондта. Нехай сукупність n спостережень упорядкована по мірі зростання однієї з незалежних змінних. Розіб'ємо її на дві групи об’ємами n 1 і n 2, виключивши приблизно чверть середніх значень. Побудуємо 2 р егресії по перших По кожній з груп будують регресію і знаходять відношення: Якщо вони менше 1, то групи міняють місцями. Це значення слід порівняти з теоретичним F teor = F (n 1 – k,n 2 – k,1 −α). Якщо F pr < F teor, то збурення гомоскедастичні, в протилежному випадку – гетероскедастичні. 38. Тест Глейзера…. Критерій Уайта 40. Зважений метод найменших квадратів бла бла бла… 41. Сутність автокореляції, її природа, причини виникнення і наслідки Одним з основних припущень класичного лінійного регресійного аналізу є припущення щодо відсутності взаємозв’язку між значеннями стохастичної складової моделі ε в різних спостереженнях, тобто припущення
Якщо це припущення порушується - виникає явище, яке носить назву автокореляції залишків. Оцінка Дарбіна-Уотсона. Метод Дарбіна. Формула (*) записується у вигляді тобто y t −1 включається в число регресорів, а ρ – в число параметрів, що оцінюються. Для цієї регресії за допомогою звичайного МНК знаходяться оцінки ˆ ρ та ˆθ j параметрів ρ та ρβ j відповідно. В якості оцінки ˆ β j беруть ˆθ j / ˆ ρ. Можна покращити якість оцінок ˆ β j, підставивши отримане значення ˆ ρ до (*), і знайти нові МНК-оцінки параметрів ˆβ j. Метод Кочрейна-Оркатта. Ітеративно обраховуються формули (*),
найменших квадратів, поки не буде досягнуто необхідної точності. Метод Хілдрета-Лу. Обчислюється модель при всіх ρ з інтервалу від -1 до 1 з кроком 0.01. Вибирається те значення, при якому сума квадратів відхилень в узагальненому Методі найменших квадратів мінімальна.
Критерій Дарбіна Уотсона Оскільки автокореляція є негативним явищем, потрібно вміти його тестувати. Найбільш відомим і поширеним тестом перевірки моделі на наявність автокореляції залишків є тест Дарбіна-Уотсона. Цей тест використовується для авторегресійних схем 1-го порядку і має наступний алгоритм. Метод Дарбіна Метод Дарбіна. Формула (*) записується у вигляді тобто y t −1 включається в число регресорів, а ρ – в число параметрів, що оцінюються. Для цієї регресії за допомогою звичайного МНК знаходяться оцінки ˆ ρ та ˆθ j параметрів ρ та ρβ j відповідно. В якості оцінки ˆβ j беруть ˆθ j / ˆ ρ. Можна покращити якість оцінок ˆ β j, підставивши отримане значення ˆ ρ до (*), і знайти нові МНК-оцінки параметрів ˆβ j. Метод Дарбіна. Формула
Метод Хілдрета-Лу. Обчислюється модель при всіх ρ з інтервалу від -1 до 1 з кроком 0.01. Вибирається те значення, при якому сума квадратів відхилень в узагальненому методі найменших квадратів мінімальна. Модель попиту та пропозиції Qdt= γ0+ γ1pt+ γ2yt+ε1t Qst=β0+ β1pt+ β2Zt Qdt= Qst <= система (все 3 уравнения). pt-ціна товару; yt – особистий дохід; Zt – неціновий фактор; Якщо попит зростає, то пропозиція, також, зростає. Ціна товару pt залежить від ε1t. Двоетапний МНК. Алгоритм. Системою одночасних економетричних рівнянь називається сист, в якій одні і ті ж залежні змінні в одних рівняннях входять до лівої частини, а в інших – до правої частини. В них розрізняють: Ендогенні змінні – взаємозалежні змінні, які визначаються всередині моделі. Екзогенні змінні – незалежні змінні, які визначаються зовні системи. До групи предетермінованих змінних також включають лагові значення ендогенних змінних (значення ендогенних змінних в попередні моменти часу). Двоетапний МНК використовується для оцінки надідентифікованих рівнянь у системах одночасних р-нь. Необхідна умова ідентифікації. D + 1 = H – рівняння ідентифіковане, D + 1 < H – рівняння неідентифіковане, D + 1 > H – рівняння надідентифіковане, де D – кількість предетермінов змінних, що відсутні в рів-ні, але присутні в системі, H – кількість ендогенних змінних в рівнянні. Алгоритм методу: 1. За допомогою звичайного методу найменших квадратів оцінюється регресія кожної ендогенної змінної відносно набору всіх екзогенних змінних системи. 2. Замість ендогенних змінних, що входять у праву частину рівняння, підставляються їх оцінки, знайдені на першому етапі. Одержані рівняння оцінюються за допомогою звичайного методу найменших квадратів. Звичайний МНК: знаходження параметрів регресії:
Можна також скористатися готовими формулами:
Вибіркова регресійна функція має вигляд: Залишки моделі знаходяться за формулою:
Лаговий оператор. Аналізуючи часові ряди, зручно використовувати оператор лага (В або L), за допомогою якого можна отримувати значення часового ряду як функції від його інших значень. Буквально лаг означає запізнення і мається на увазі значення змінної у попередній період. Часто використання лагового оператору прихводить до втрати математичної строгості, але воно значно спрощує математичні обчислення. До лагового оператору можна застосовувати усі еретворення, що і до звичайної змінної. Застосувавши В для знач. yt, отримаємо yt-1, тобто Вyt = yt-1. Оператор лага можна застосовувати рекурентно: В(Вyt)=Вyt-1 = yt-2 Якщо оператор лага діє k>0 разів, то число k записують як показник степеня: Вkyt=B(Вk-1yt)= yt-k Нарешті: В0yt= yt Можна утворювати поліноми від оператора лага:
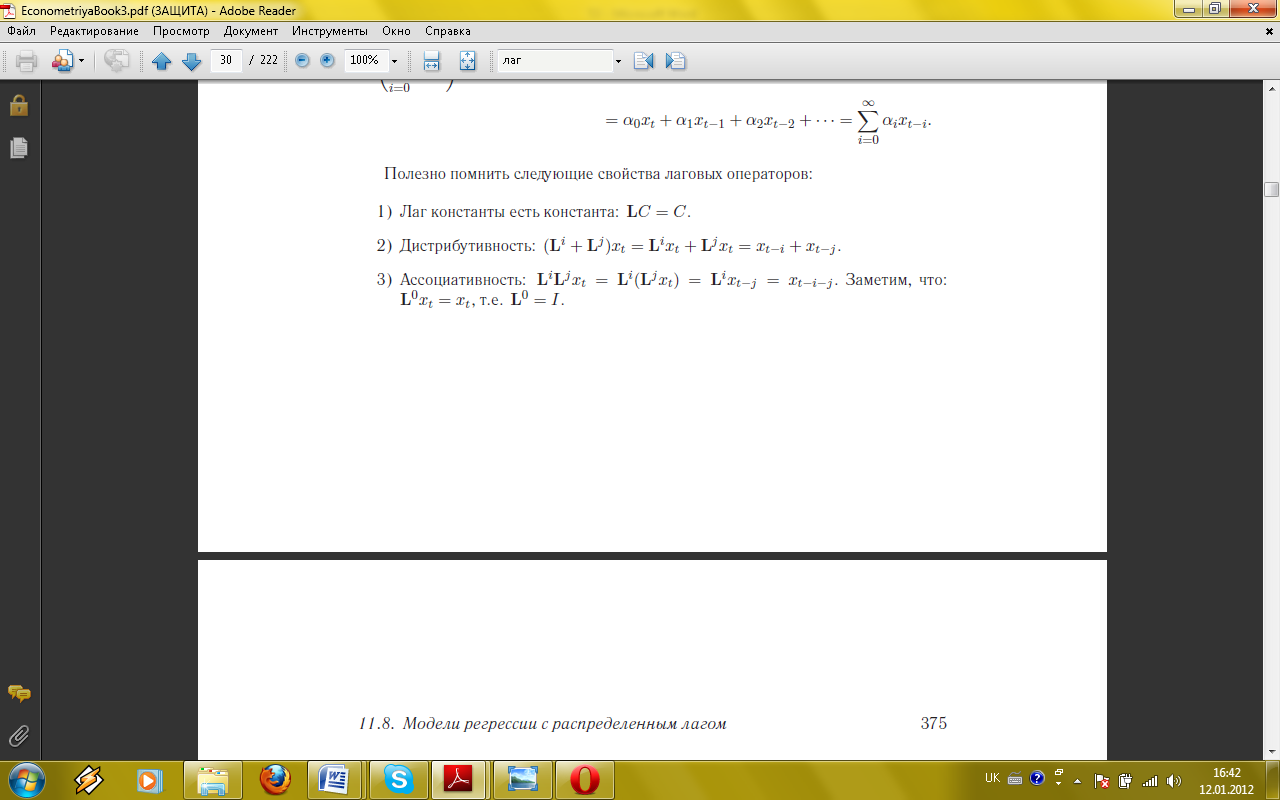
Відомі наступні властивості лагового оператору: 1) В С = С (лаг константи дорівнює константі) 2) Дистрибутивність:
3) Асоціативність: 4) Відємний лаг:
Міри точності прогнозів
Про точність прогнозу зазвичай судять за розміром помилки прогнозу - різниці між прогнозним і фактичним значенням досліджуваної змінної. Проте такий підхід до оцінювання точності можливий лише якщо дослідник має фактичні значення змінної. Отримані ретроспективно помилки прогнозу якоюсь мірою характеризують точність застосованої методики прогнозування і можуть виявитися корисними під час зіставляння кількох методів. Водночас розмір помилки ретроспективного прогнозу не можна розглядати як остаточний доказ придатності або, навпаки, непридатності застосовуваного методу прогнозування. Перевірка точності одного прогнозу мало що може сказати. Гарний одиничний прогноз можна отримати і за поганою моделлю, і навпаки. Звідси випливає, що про якість прогнозів застосовуваних методик і моделей можна судити лише за сукупністю зіставлень прогнозів і їхньої реалізації. Найбільш простою мірою якості прогнозів за умови, що є дані про їхню реалізацію, може стати відношення кількості випадків, коли фактичну реалізацію охоплював інтервальний прогноз, до загальної кількості прогнозів, тобто
де т - кількість прогнозів, підтверджених фактичними даними; р - кількість прогнозів, не підтверджених фактичними даними. Коли всі прогнози підтверджуються, то р = 0 і Г) = 1; якщо ж усі прогнози не підтвердилися, то т, а отже, і г| дорівнюють 0. Міра якості прогнозу Г. Тейла: коефіцієнт розбіжності, чисельником якого є середньоквадратична похибка прогнозу, а знаменник дорівнює квадратному кореню із середнього квадрата реалізації, тобто
де р - кількість періодів, на які розраховують прогноз. Коефіцієнт V=0, коли всі уt prong= уt (випадок ідеального прогнозування); V = 1, коли процес прогнозування призводить до середньоквадратичної помилки "наївної" екстраполяції незмінності приростів; нарешті, V > 1, коли прогноз дає гірші результати, ніж припущення про незмінність досліджуваного явища. Верхньої межі коефіцієнт не має. Коефіцієнт розбіжності можна використати під час зіставляння якості прогнозів, одержаних на основі різноманітних методів і моделей. У цьому його безсумнівна привабливість. Також виокремлюють більш об'єктивні статистики точності прогнозів: МSЕ, RМSЕ, МАD, RМSPЕ, МАРЕ. Нехай yt_pr - прогноз значення часового ряду у t-му періоді, тоді:
- середня абсолютна похибка за р кроків
-
- за р кроків.
На практиці ці характеристики використовують досить часто. Перші три критерії виражають похибку в одиницях виміру, тому їхня величина залежить від специфіки часового ряду. Останні два критерії вимірюються у відносних одиницях, тому можна говорити про деякий загальний рівень адекватності моделі на основі їх порівняння.
Метод усереднення
Одним із методів згладжування часового ряду є метод рухомого середнього (усереднення). Суть полягає у заміні початкового часового ряду послідовністю середніх, що обчислюються на відрізку, який переміщується вздовж часового ряду. Задається довжина відрізка ковзання (2m+1) по часовій осі, тобто береться непарна кількість спостережень. Підбирається поліном: Для визначення коефіцієнтів a0, a1,..., ар полінома за допомогою методу найменших квадратів за першим (2 m + 1) точкам мінімізується функціонал:
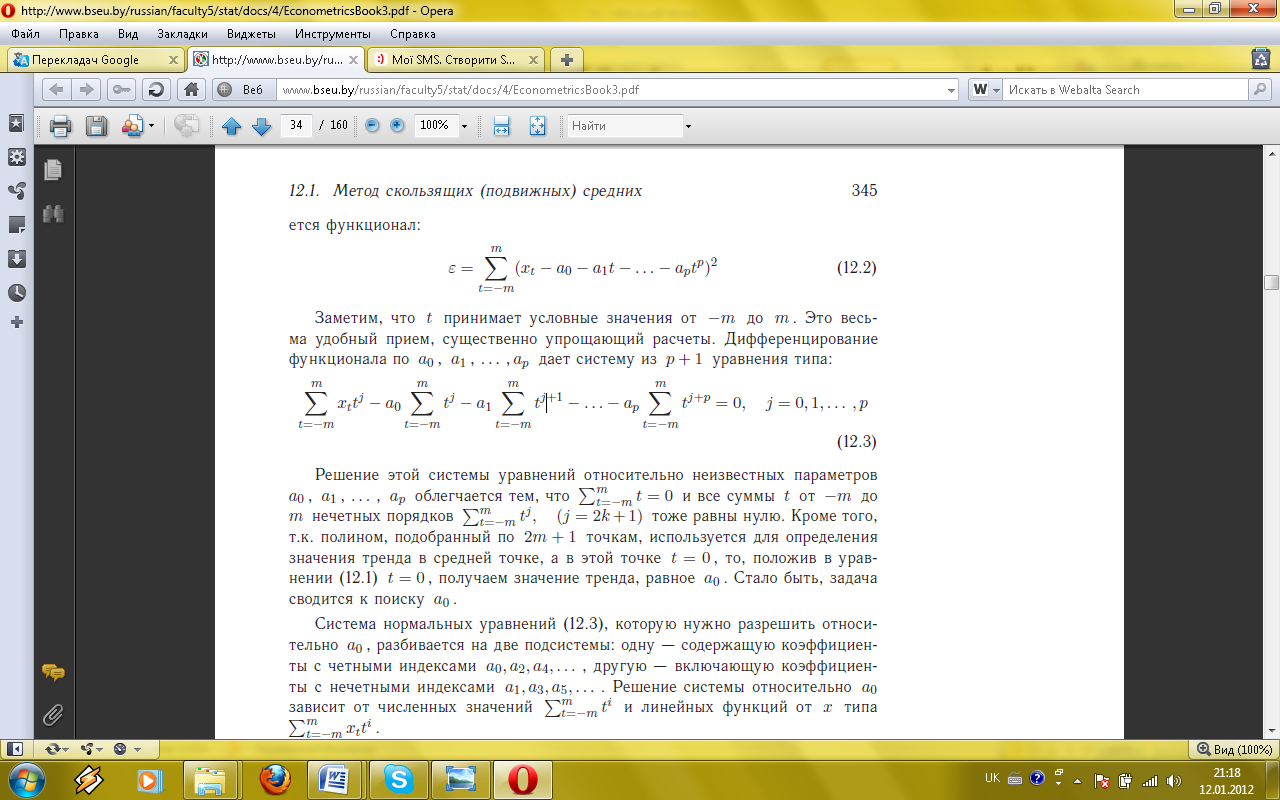
Зауважимо, що t приймає умовні значення від-m до m. Це досить зручний прийом, істотно спрощує розрахунки. Диференціювання функціоналу по a0, a1,..., ар дає систему з р + 1 рівняння типу:
Рішення цієї системи рівнянь щодо невідомих параметрів a0, a1,..., ар полегшується тим, що Система нормальних рівнянь, яку потрібно вирішити відносно а0, розбивається на дві підсистеми: одна - містить коефіцієнти з парними індексами а0, а2, а4,..., Інша - включає коефіцієнти з непарними індексами а1, а3, а5,.... Рішення системи щодо a0 залежить від чисельних значень У підсумку, значенням тренда в центральній точці відрізка буде середня арифметична, зважена із значень часового ряду від х-м до хм з ваговими коефіцієнтами βt, які залежать від значень м і р: Зазначена процедура повторюється для всіх наступних відрізків ковзання, з обчисленням значень тренду в їх середніх точках.
Визначення економетрії як науки, її природа. Приклади використання економетричних моделей для розв’язування економічних задач. Економетрика – наука, що вивчає економічні моделі та процеси за допомогою математичних та статистичних методів.-конспект Економетрика (за підр. Черняка) – наука, що вивчає кількісні взаємозв’язки економічних об’єктів і процесів за допомогою математичних і статистичних методів і моделей. Економетричні методи передбачають статистичний аналіз конкретних економічних даних зазвичай за допомогою комп’ютерів. Також, можна описати економетрику, як галузь економічної теорії, яка вивчає моделі економічних систем у такій формі, яка дає можливість перевіряти ці моделі на адекватність засобами математичної статистики. Основна задача економетрики полягає в практичній перевірці основних економічних концепцій та положень.-конспект Економетрика – наука, яка вивчає конкретні кількісні та якісні взаємозв’язки економічних процесів за допомогою математичних та статистичних методів та моделей. Мета економетрики – здійснювати емпіричну перевірку положень економічної теорії, підтверджуючи чи відхиляючи останні. Цим економетрика відрізняється від математичної економіки, зміст якої полягає виключно у застосуванні математики, і теоретичні положення якої не обов’язково потребують емпіричного підтвердження. Економетрика є результатом синтезу економічної теорії, математичної статистики та економічної статистики. Застосування статистичних методів до аналізу економічних даних має давню історію. Перша «емпірична» крива попиту була опублікована Чарльзом Дейвенентом у 1699 році. Економічна модель являє собою набір припущень, які приблизно описують поведінку економіки (або сектора економіки). Економетрична модель складається з таких частин: 1). Набір рівнянь поведінки, які виводяться з економічної моделі. Ці рівняння включають деякі змінні, значення яких спостерігаються, а також «збурення», які відтворюють ефект від змінних, не включених до моделі у явному вигляді, та ефект від непередбачуваних подій. 2). Опис імовірнісного розподілу «збурень». Економетричні моделі мають стохастичний характер. Розглянемо співвідношення між споживанням С та доходом Y у такому вигляді: С = α + β Y + ε, де ε – збурення, або стохастична складова моделі, α і β – невідомі параметри, які можна оцінити за допомогою методів математичної статистики. Стохастичний характер економетричних моделей дозволяє використовувати теорію статистичних висновків для перевірки цих моделей на адекватність. Перевірка складається з двох етапів: статистичного і економічного. На статистичному етапі ми перевіряємо, чи виконуються вимоги, які накладено на стохастичну складову ε при формулюванні моделі. На економічному етапі ми перевіряємо, чи узгоджуються знайдені оцінки параметрів з положеннями економічної теорії. Наприклад, теорія споживання стерджує, що зі зростанням доходу споживання зростає, але не в такій мірі як доход. Звідси випливає, що ця модель коректна, при 0 < β < 1. Таким чином, економетричні методи дозволяють не тільки встановлювати кількісні зв’язки між економічними змінними, але й робити висновки про коректність одержаних моделей.
2. Роль економетричних досліджень в економіці. Роль економетричного дослідження визначається тими задачами, які може розв’язувати економетрія. Найважливішою задачею є оцінювання параметрів і перевірка значущості економетричної моделі. Етапи економетричного дослідження: 1) Формування економічної концепції чи гіпотези 2) Збір упорядкованої інформації та необхідних даних 3) Розрахунок моделі та перевірка її адекватності 4) Аналіз моделі, розробка прогнозів, перевірка економетричних тестів Структуру економетричних досліджень:
В сучасних умовах роль економетричних досліджень є значною. Відбувається розробка нових методів оцінювання параметрів моделей з урахуванням особливостей вихідної економічної інформації, а також розширення економічних досліджень на основі економетричних методів. Пояснення та аналіз актуальних економічних процесів та проблем невід’ємно пов’язано із використанням математичних методів. Саме вони забезпечують найбільш чітку та повну характеристику стану економіки й допомагають прийняти необхідні рішення для підвищення ефективності функціонування господарства країни.
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 847; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.95.167 (0.019 с.) |


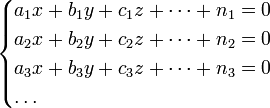
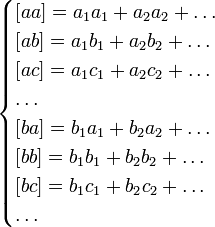
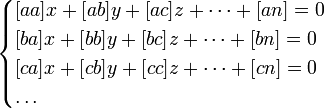


 . (1.17а)
. (1.17а) до 1, тим точніше x пояснює y. Якщо
до 1, тим точніше x пояснює y. Якщо 


 .
.
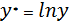
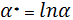
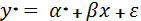
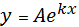
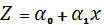
 =lnA,
=lnA, 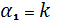
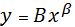
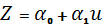
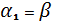
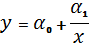
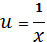



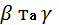 , тому цю модель неможна звести до простої лінійної регресії.
, тому цю модель неможна звести до простої лінійної регресії.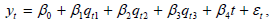
 . (7.1)
. (7.1) залишки за узагальненим методом
залишки за узагальненим методом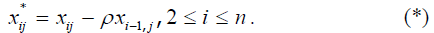 записується у вигляді
записується у вигляді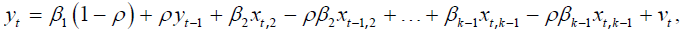
 . Метод Кочрейна-Оркатта. Ітеративно обраховуються формули:
. Метод Кочрейна-Оркатта. Ітеративно обраховуються формули: 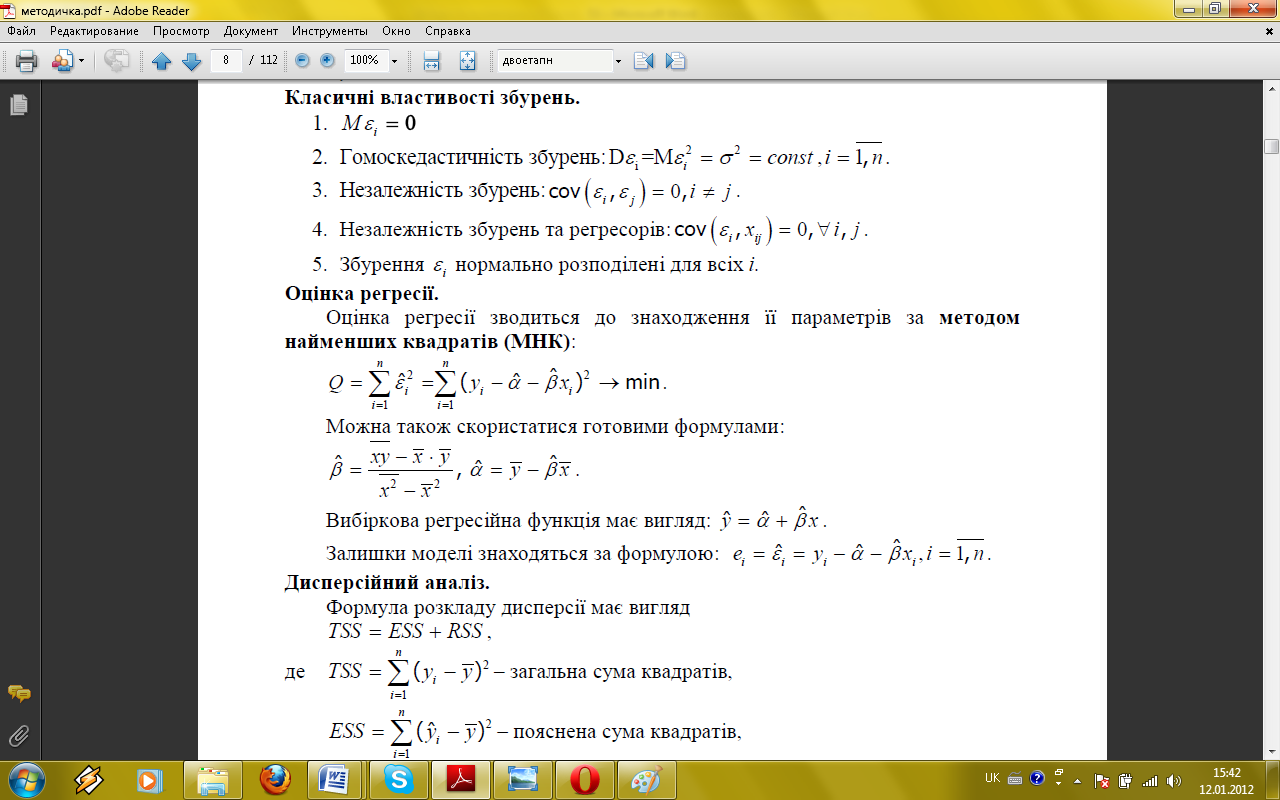
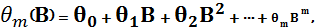
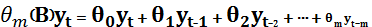


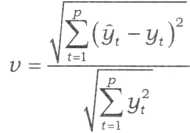
 Середньоквадратична похибка прогнозу за р кроків;
Середньоквадратична похибка прогнозу за р кроків; - корінь із середньокв-ї похибки
- корінь із середньокв-ї похибки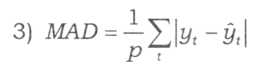
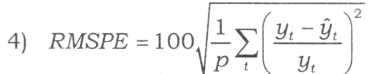 корінь із середньокв-ї похибки у відсотках від фактичних значень
корінь із середньокв-ї похибки у відсотках від фактичних значень середня абсолютна похибка у відсотках
середня абсолютна похибка у відсотках до групи перших (2m+1) членів ряду, і цей поліном використовується для визначення значення тренду у середній (m+1)-й точці групи. Потім провадиться зсув на один рівень ряду вперед і підбирається поліном того ж порядку до групи точок, що складається з 2-го, 3-го,..., (2 m +2)-го спостереження. Знаходиться значення тренда в (m +2)-й точці і т.д. тим же способом уздовж всього ряду до останньої групи з (2m +1) спостереження. Насправді немає необхідності будувати поліном для кожного відрізка. Як буде показано, ця процедура еквівалентна знаходженню лінійної комбінації рівнів часового ряду з коефіцієнтами, які можуть бути визначені раз і назавжди і залежать тільки від довжини відрізка ковзання і ступеня полінома.
до групи перших (2m+1) членів ряду, і цей поліном використовується для визначення значення тренду у середній (m+1)-й точці групи. Потім провадиться зсув на один рівень ряду вперед і підбирається поліном того ж порядку до групи точок, що складається з 2-го, 3-го,..., (2 m +2)-го спостереження. Знаходиться значення тренда в (m +2)-й точці і т.д. тим же способом уздовж всього ряду до останньої групи з (2m +1) спостереження. Насправді немає необхідності будувати поліном для кожного відрізка. Як буде показано, ця процедура еквівалентна знаходженню лінійної комбінації рівнів часового ряду з коефіцієнтами, які можуть бути визначені раз і назавжди і залежать тільки від довжини відрізка ковзання і ступеня полінома.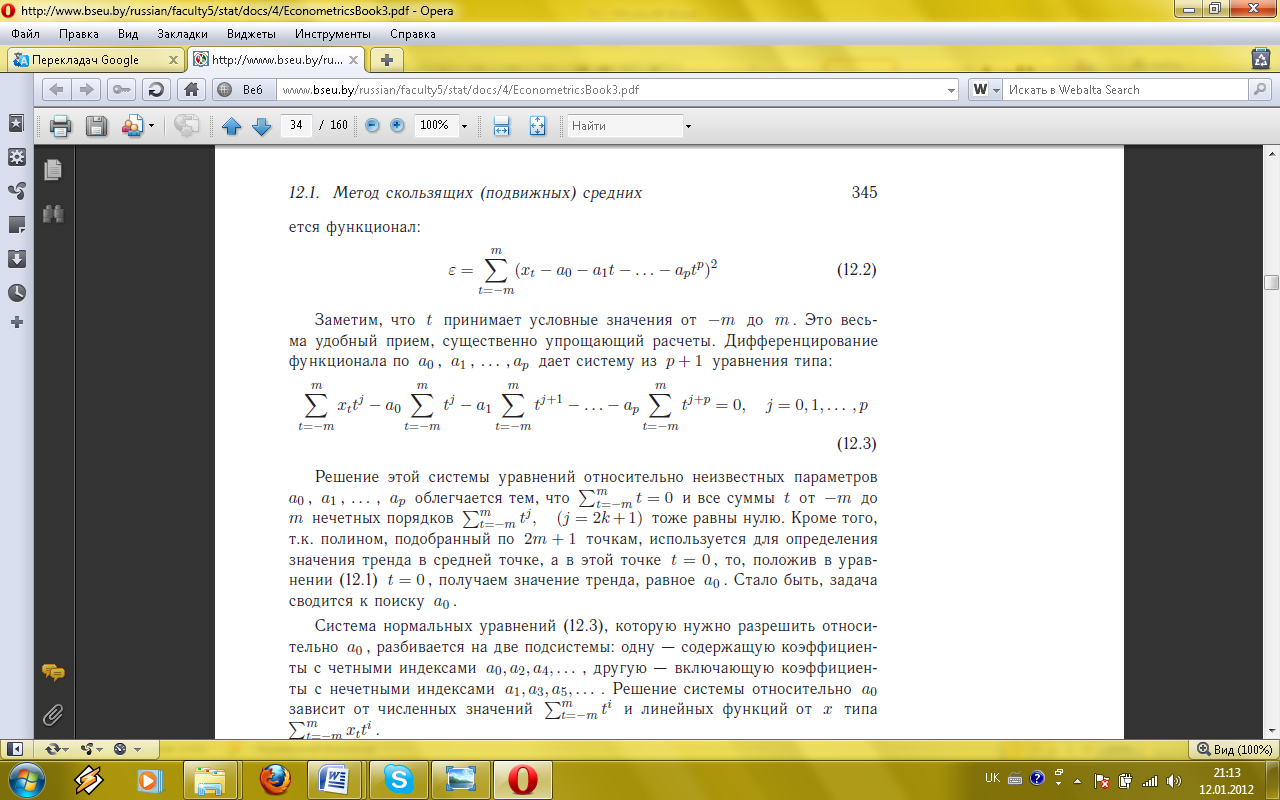
 і всі суми від t-m до m непарних порядків
і всі суми від t-m до m непарних порядків 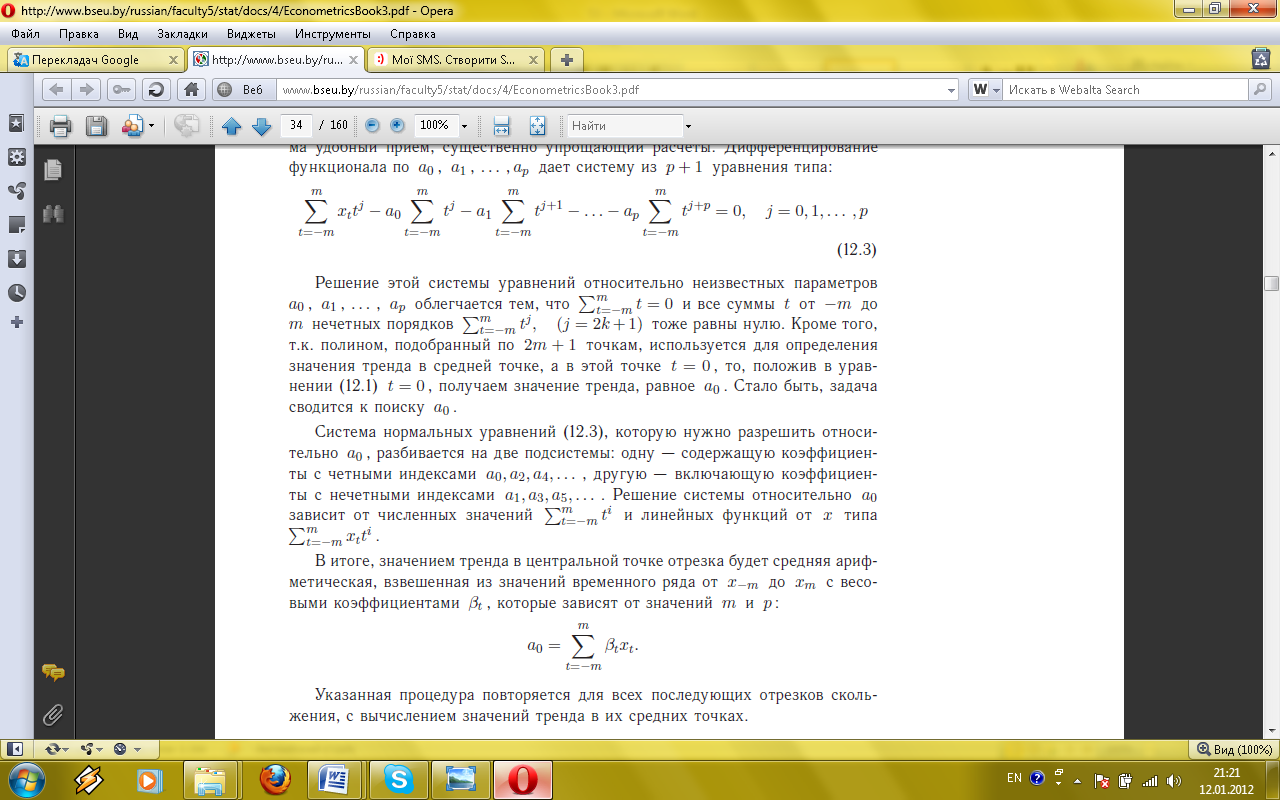 теж рівні нулю. Крім того, т.я. поліном, підібраний за 2m +1 точками, використовується для визначення значення тренда в середній точці, а в цій точці t = 0, то, поклавши в рівняння t = 0, отримуємо значення тренда, рівне а0. Стало бути, завдання зводиться до пошуку а0.
теж рівні нулю. Крім того, т.я. поліном, підібраний за 2m +1 точками, використовується для визначення значення тренда в середній точці, а в цій точці t = 0, то, поклавши в рівняння t = 0, отримуємо значення тренда, рівне а0. Стало бути, завдання зводиться до пошуку а0.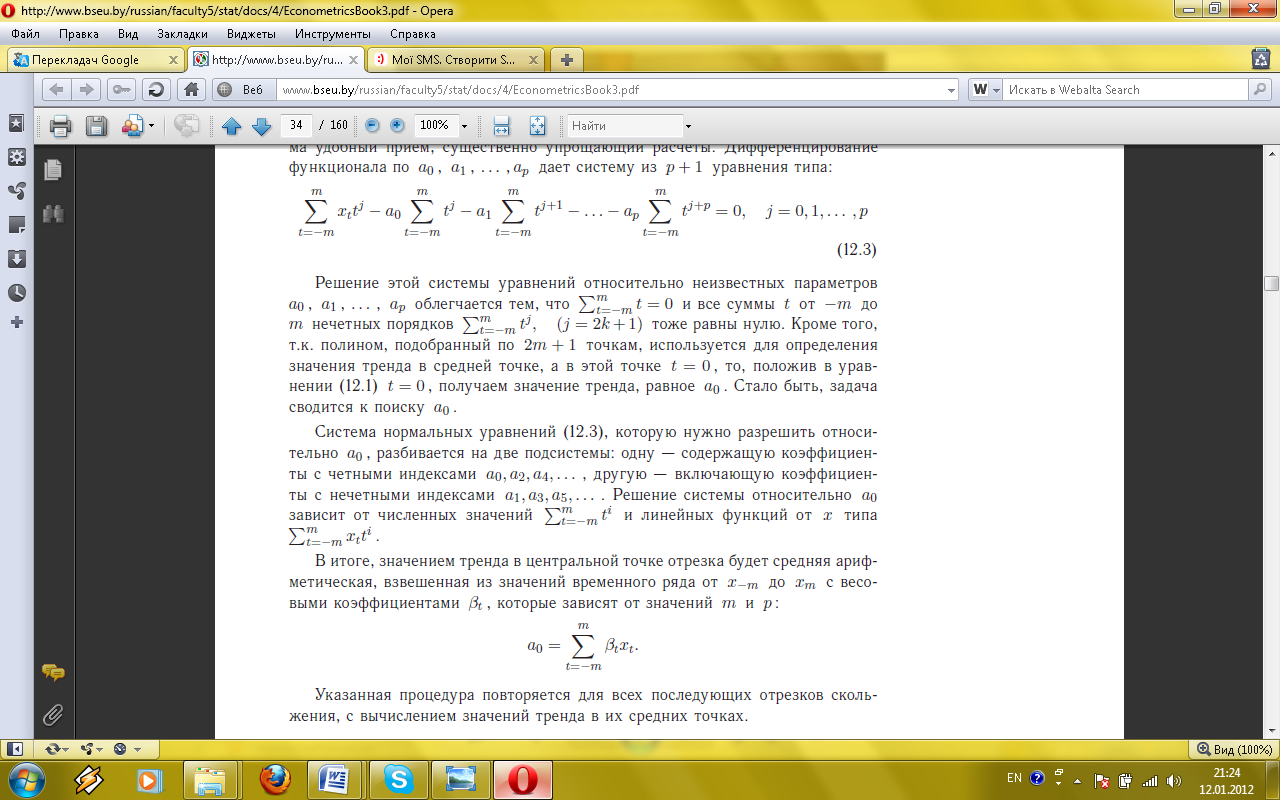 лінійних функцій від х типу
лінійних функцій від х типу