
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття гомо- й гетероскедастичності, природа гетероскедастичності.Содержание книги
Поиск на нашем сайте
Розглянемо особливості економетричного моделювання, коли порушується умова, згідно з якою припускається, що відхилення мають такий розподіл імовірностей, який зберігається для всіх спостережень. Тоді дисперсія залишків лишається незмінною для кожного спостереження. Означення 7.1. Якщо дисперсія залишків стала для кожного спостереження, тобто Часто у практичних дослідженнях явище гомоскедастичності порушується. Випробування на наявність чи відсутність гомоскедастичності звичайно не практикується, але здебільшого можна висунути гіпотези про правдоподібність альтернативних припущень щодо пропорційності помилки до X. Так, наприклад, при побудові економетричної моделі, що характеризує залежність між заощадженнями і доходами населення на підставі теоретичної та практичної інформації, можна висунути гіпотезу, що дисперсія залишків за окремими групами населення змінюватиметься і буде пропорційною до середнього доходу цієї групи. Коли розглядати економетричну модель, що характеризує залежність між дивідендами і розміром прибутку або між витратами на харчування і доходом на одного члена сім’ї, витратами на харчування і загальними витратами, то також можна припустити, що дисперсія залишків для окремих груп спостережень змінюватиметься. Означення 7.2. Якщо дисперсія залишків змінюється для кожного спостереження або групи спостережень, тобто Якщо існує гетероскедастичність залишків, то це спричинюється до того, що оцінки параметрів моделі 1МНК будуть незміщеними, обгрунтованими, але неефективними. При цьому формулу для стандартної помилки оцінки, строго кажучи, застосувати не можна. припустимо, що дисперсія залишків для моделі . У результаті для оцінювання параметрів можна застосувати МНК. Зауважимо, що параметри а 0 і а 1 помінялися ролями. Вільним членом моделі замість а 0 став параметр а 1. Метод перевірки гетероскедастичності на основі тесту Голдфелда-Квондта Модель лінійної регресії з гетероскедастичними збуреннями Основні визначення Вид моделі. в якій вектор збурень не задовольняє класичним властивостям збурень: 1. Mv i = 0 2. Гетероскедастичність збурень: 3. Незалежність збурень: 4. Незалежність збурень та регресорів: 5. Збурення v i нормально розподілені для всіх i. Наслідки гетероскедастичності збурень на оцінки методу найменших квадратів: 1.Оцiнки МНК будуть незміщеними, але не будуть ефективними (не матимуть найменшої дисперсії). 2.Стандартнi оцінки коварiацiйної матриці оцінки МНК будуть зміщеними, i, як наслідок, процедури перевірки гіпотез та інтервального оцінювання, основані на стандартних статистиках, будуть некоректними. Критерії виявлення гетероскедастичності Критерій Голдфелда-Квондта. Нехай сукупність n спостережень упорядкована по мірі зростання однієї з незалежних змінних. Розіб'ємо її на дві групи об’ємами n 1 і n 2, виключивши приблизно чверть середніх значень. Побудуємо 2 р егресії по перших По кожній з груп будують регресію і знаходять відношення: Якщо вони менше 1, то групи міняють місцями. Це значення слід порівняти з теоретичним F teor = F (n 1 – k,n 2 – k,1 −α). Якщо F pr < F teor, то збурення гомоскедастичні, в протилежному випадку – гетероскедастичні. 38. Тест Глейзера…. Критерій Уайта 40. Зважений метод найменших квадратів бла бла бла… 41. Сутність автокореляції, її природа, причини виникнення і наслідки Одним з основних припущень класичного лінійного регресійного аналізу є припущення щодо відсутності взаємозв’язку між значеннями стохастичної складової моделі ε в різних спостереженнях, тобто припущення
Якщо це припущення порушується - виникає явище, яке носить назву автокореляції залишків.
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 613; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.140.108 (0.009 с.) |

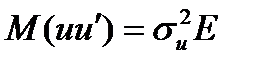 , то ця її властивість називається гомоскедастичністю.
, то ця її властивість називається гомоскедастичністю. , то це явище називається гетероскедастичністю.
, то це явище називається гетероскедастичністю.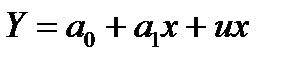 пропорційна до величини Х. Тоді доцільно виконати перетворення вихідної інформації, поділивши, наприклад, усі змінні на Х. Модель набере вигляду
пропорційна до величини Х. Тоді доцільно виконати перетворення вихідної інформації, поділивши, наприклад, усі змінні на Х. Модель набере вигляду
 . (7.1)
. (7.1)


