
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм тесту Дарбіна - УотсонаСодержание книги
Поиск на нашем сайте
Крок 1. Виходячи з відсутності автокореляції залишків на основі методу найменших квадратів будується економетрична модель і обчислюються її залишки Крок 2. Розраховується статистика (критерій) Дарбіна-Уотсона за наступною залежністю
Крок 3. Задаючись рівнем значимості a, для числа факторів моделі m і числа спостережень n за статистичними таблицями DW - розподілу Дарбіна-Уотсона, визначаються два значення dL, і dU. Крок 4. Будуються зони автокореляційного зв’язку, які схематично можна представити в наступному вигляді:
Рис. 7.2 - Зони автокореляційного зв’язку Крок 5. На основі розрахункового значення критерію DW роблять висновок щодо наявності або відсутності автокореляції залишків: · якщо · якщо · якщо · якщо Метод Дарбіна Метод Дарбіна. Формула (*) записується у вигляді тобто y t −1 включається в число регресорів, а ρ – в число параметрів, що оцінюються. Для цієї регресії за допомогою звичайного МНК знаходяться оцінки ˆ ρ та ˆθ j параметрів ρ та ρβ j відповідно. В якості оцінки ˆβ j беруть ˆθ j / ˆ ρ. Можна покращити якість оцінок ˆ β j, підставивши отримане значення ˆ ρ до (*), і знайти нові МНК-оцінки параметрів ˆβ j. Узагальнений метод найменших квадратів у випадку відомої кореляційної матриці збурень. Узагальнений метод найменших квадратів. Будемо вважати, що для регресії y = X β + v (1) кореляційна матриця Σ відома. Введемо наступні позначення:
З урахуванням уведених позначень маємо: y * = X *β +ε (2). Оцінкою узагальненого МНК коефіцієнтів моделі (1) називається оцінка звичайного МНК, знайдена за моделлю (2).
Авторегресія першого порядку Процес авторегресії першого порядку AR(1).
У випадку AR(1)–збурень кореляційна матриця Σ записується у вигляді
Це дає можливість знайти змінні для узагальненого методу найменших
Якщо у вихідній моделі є постійний доданок, то перетворена модель не матиме константи. Замість неї з’явиться змінна
Оцінювання моделі з автокорельованими збуреннями у випадку невідомої кореляційної матриці збурень. Для того, щоб застосувати МНК у випадку AR(1) збурень нам не вистачає оцінки коефіцієнта ρ. Оцінка параметра ρ. Вибірковий коефіцієнт кореляції залишків методу найменших квадратів
Метод Дарбіна. Формула
Метод Хілдрета-Лу. Обчислюється модель при всіх ρ з інтервалу від -1 до 1 з кроком 0.01. Вибирається те значення, при якому сума квадратів відхилень в узагальненому методі найменших квадратів мінімальна. Системи одночасних структурних рівнянь. Перехід до зведеної форми, їх взаємозв’язок. Системою взаємопов'язаних одночасних економетричних рівнянь називається система, в якій одні і ті ж залежні змінні в одних рівняннях входять до лівої частини, а в інших – до правої частини. Наприклад, в моделі Клейна.
де капітал, Структурний вигляд системи одночасних рівнянь. У структурному вигляді системи одночасних рівнянь кожне рівняння відображає певний елемент структури економічної системи, що розглядається, і має економічну інтерпретацію. Характерною особливістю структурних рівнянь є їх певна автономність щодо визначених змінних, оскільки зміна останніх в одному структ. рівнянні не обов’язково зумовлює зміну залежних змінних в інших рівн.х.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.59.252 (0.009 с.) |

 .
. (7.8)
(7.8) - це свідчить про наявність позитивної автокореляції залишків;
- це свідчить про наявність позитивної автокореляції залишків; - це свідчить про наявність негативної автокореляції залишків;
- це свідчить про наявність негативної автокореляції залишків; - неможливо зробити висновок ні про наявність, ні про відсутність автокореляції залишків;
- неможливо зробити висновок ні про наявність, ні про відсутність автокореляції залишків; - автокореляція залишків відсутня.
- автокореляція залишків відсутня.


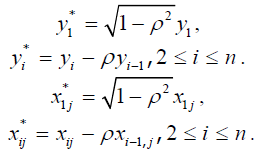 квадратів у явному вигляді:
квадратів у явному вигляді: , значення якої дорівнюють
, значення якої дорівнюють
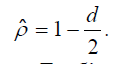
 Оцінка Дарбіна-Уотсона.
Оцінка Дарбіна-Уотсона.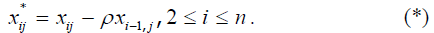 записується у вигляді
записується у вигляді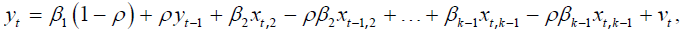
 . Метод Кочрейна-Оркатта. Ітеративно обраховуються формули:
. Метод Кочрейна-Оркатта. Ітеративно обраховуються формули:  , залишки за узагальненим методом найменших квадратів, поки не буде досягнуто необхідної точності.
, залишки за узагальненим методом найменших квадратів, поки не буде досягнуто необхідної точності.
 – інвестиції,
– інвестиції,  – споживання,
– споживання, 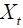 – чистий експорт,
– чистий експорт,  – зарплата у приватному секторі,
– зарплата у приватному секторі,  – зарплата у державному секторі,
– зарплата у державному секторі,  – державні видатки, що не включають зарплату,
– державні видатки, що не включають зарплату,  – доход від приватного сектора,
– доход від приватного сектора,  –
– – ВВП країни у період t,
– ВВП країни у період t,  – тренд.
– тренд.


