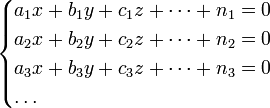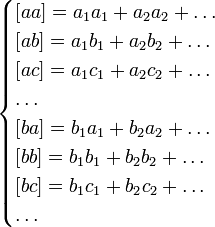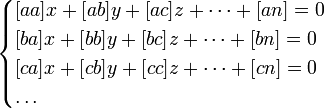Загальний вигляд лінійної економетричної моделі та етапи її побудови

Общий вид нормальной (традиционной или классической) линейной модели парной (однофакторной) регрессии

yi=β0+β1xi+εi,

где yi– результативные переменные,

xi – факторные переменные,

β0, β1 – параметры модели регрессии, подлежащие оцениванию;

εi – случайная ошибка модели регрессии.

При построении нормальной линейной модели парной регрессии учитываются пять условий:

1) факторная переменная xi – неслучайная или детерминированная величина, которая не зависит от распределения случайной ошибки модели регрессии εi;

2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:

3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений.

4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю): Cov(εi,εj)=E(εi,εj)=0 (). Это условие выполняется в том случае, если исходные данные не являются временными рядами;

5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2: εi~N(0, G2).

 

Специфікація економетричної моделі

 

9. Передумови застосування методу найменших квадратів (МНК).

При наявності n спостережень модель множинної лінійної регресії записується у вигляді

де x_ij – значення j -ї незалежної змінної (x_j) в i -му спостереженні, збурення e _i задовольняють тим самим припущенням, що і в моделі простої регресії.

1. Нульове середнє: Me _i = 0, .

2. Рівність дисперсій: De _i = E = s² = const, .

3. Незалежність збурень: e _і та e _j незалежні при .

4. Незалежність збурень та регресорів: x_ij та e _і незалежні для всіх i та j (якщо регресори не стохастичні, то дане припущення виконується автоматично).

5. (Додаткове). Збурення e _i нормально розподілені для всіх i.

5. Модель является линейной относительно параметров

МНК

Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки.

Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов

Пусть надо решить систему уравнений (1)

Чтобы решить их по способу наименьших квадратов, составляют новую систему уравнений, число которых равно числу неизвестных и которые затем решаются по обыкновенным правилам алгебры. Эти новые, или так называемые нормальные уравнения составляются по следующему правилу: умножают сперва все данные уравнения на коэффициенты у первой неизвестной x и, сложив почленно, получают первое нормальное уравнение, умножают все данные уравнения на коэффициенты у второй неизвестной y и, сложив почленно, получают второе нормальное уравнение и т. д.

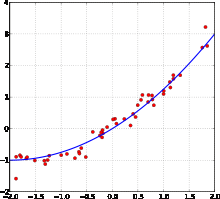
Пример кривой, проведённой через точки, имеющие нормально распределённое отклонение от истинного значения.

то нормальные уравнения представятся в следующем простом виде: (2)

11. Властивості статистичних оцінок параметрів, їх характеристика.

При оцінюванні бажано, щоб втрата інформації, яка може бути суттєвою для прийняття статистичних рішень, була мінімальною. Отже, для того, щоб оцінки були надійними, вони мають відповідати деяким вимогам, тобто володіти певними властивостями.

Основними властивостями статистичних оцінок є спроможність, незмі-щенність, ефективність:

o Спроможність. Статистична оцінка ®n спроможна тоді, коли при постійному збільшенні обсягу вибірки (n -"со) вона наближається до значення параметра ©, який оцінює. Статистика ©" є спроможною оцінкою параметpa 0, коли для будь-якого додатного числа є є справедливим співвідношення

limP{©n -0>є = 0. (4.2)

Наприклад, вибіркове середнє X є спроможною оцінкою генерального середнього fi, оскільки при збільшені числа випробувань X наближається до свого математичного сподівання (див. вираз (3.45)). Спроможною оцінкою вважається і вибіркова дисперсія.

Вимога спроможності означає, що оцінка має нести практичний сенс, наближати нас до істини і не бути абсурдною. З другого боку, у більшості ситуацій можна запропонувати декілька спроможних оцінок для одного й того ж самого параметра. Отже, властивість спроможності необхідна, але недостатня вимога. її необхідно доповнити іншими вимогами.

o Незміщенність. Статистика вважається незміщеною, якщо її математичне сподівання дорівнює параметру, що оцінюється. Вибіркове середнє X є незміщеною оцінкою генерального середнього fi, оскільки м[ X ] =ц, чого не можна сказати, наприклад, про вибіркові показники дисперсії. Для математичного сподівання можна записати

o Ефективність. Точкова оцінка називається ефективною, якщо вона має найменшу міру дисперсії вибіркового розподілу у порівнянні з аналогічними оцінками, тобто виявляє найменшу випадкову варіативність. Наприклад, серед трьох показників положення центру нормального розподілу (середнього Х, медіани ма і моди Мо) найбільш ефективною оцінкою вважається Х і найменш ефективною - Мо, оскільки для їхніх дисперсій характер-

Для статистичного оцінювання параметрів генеральної сукупності бажано використовувати оцінки, які задовольняють одночасно вимоги спроможності, незміщенності й ефективності. Крім того, важливо знати, за якими методами відбувається вибір і побудова тієї чи іншої моделі статистичного оцінювання.