
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок аналізу часових рядів. Адитивна та мультиплікативна моделіСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Часовий ряд – набір значень, що їх мала деяка змінна за послідовні та зазвичай рівні проміжки часу. Якщо прийняти довжину такого проміжку часу за одиницю часу (рік, квартал, день…), то можна вважати, що послідовні спостереження y1, y2 … yп здійснено в моменти t=1,2,…,n. При аналізі часових рядів аналізуються лише наявні спостереження без аналіз факторів впливу. Часові ряди можуть бути переривними або дискретними; моментними (знач форм-ся в даний момент) та агрегованими (підсумування значень за певний проміжок часу) При аналізі часових рядів спостереження потрібно нормувати за доп поправочного коефіцієнта (в середньому за рік, квартал…) Основною метою аналізу часових рядів є побудова моделі, на основі якої можна буде прогнозувати значення досліджуваної змінної. Порядок аналізу часових рядів: 1. Побудова графіка для того, щоб виявити тренд та його характер 2. Визначення наявності сезонних та циклічних компонентів 3. Визначення ступеня повільності або переривчастості змін послідовно 4. Вибір моделі для часового ряду, для того, щоб мінімізувати похибку Вважається, що модель підібрана адекватно, якщо залишкова компонента ряду є процесом «білого шуму»(нульове математичне сподівання, постійна дисперсія, некорельованість елементів) Залежно від характеру зв’язку компонентів динаміки розрізняють дві основні моделі: мультиплікативна модель, коли між компонентами існує зв’язок у вигляді добутку;
адитивна модель, коли між компонентами існує зв’язок у вигляді суми.
Мультиплікативному розкладу для рівнів ряду відповідає адитивний розклад для логарифмів:
Опишемо кожний компонент часового ряду окремо. Тренд характеризує довготривалу закономірну тенденцію ряду до зростання або спадання. Його наявність неважко помітити, проаналізувавши графік часового ряду. Наявність тренда в економічних часових рядах можна пояснити демографічними або технологічними змінами, а також змінами в структурі виробництва, попиту тощо. Сезонний компонент показує коливання навколо трендового компонента. Його наявність можна пояснити сезонним характером виробництва, споживання. Наприклад, у четвертому кварталі кожного року перед Новим роком значно зростає споживання товарів.
Циклічний компонент характеризує коливання навколо тренда, пов'язані з фазами бізнес-циклів1. Випадковий компонент - це те, що залишилось від часового ряду після вилучення тренда, циклічного та сезонного компонентів. Частину таких ефектів можна зарахувати до непередбачених природних катаклізмів (землетруси, пожежі, тощо), частину - до випадкових дій людей. За наявності випадкового компонента неможливо прогнозувати значення часового ряду без похибки. Лаговий оператор. Аналізуючи часові ряди, зручно використовувати оператор лага (В або L), за допомогою якого можна отримувати значення часового ряду як функції від його інших значень. Буквально лаг означає запізнення і мається на увазі значення змінної у попередній період. Часто використання лагового оператору прихводить до втрати математичної строгості, але воно значно спрощує математичні обчислення. До лагового оператору можна застосовувати усі еретворення, що і до звичайної змінної. Застосувавши В для знач. yt, отримаємо yt-1, тобто Вyt = yt-1. Оператор лага можна застосовувати рекурентно: В(Вyt)=Вyt-1 = yt-2 Якщо оператор лага діє k>0 разів, то число k записують як показник степеня: Вkyt=B(Вk-1yt)= yt-k Нарешті: В0yt= yt Можна утворювати поліноми від оператора лага:
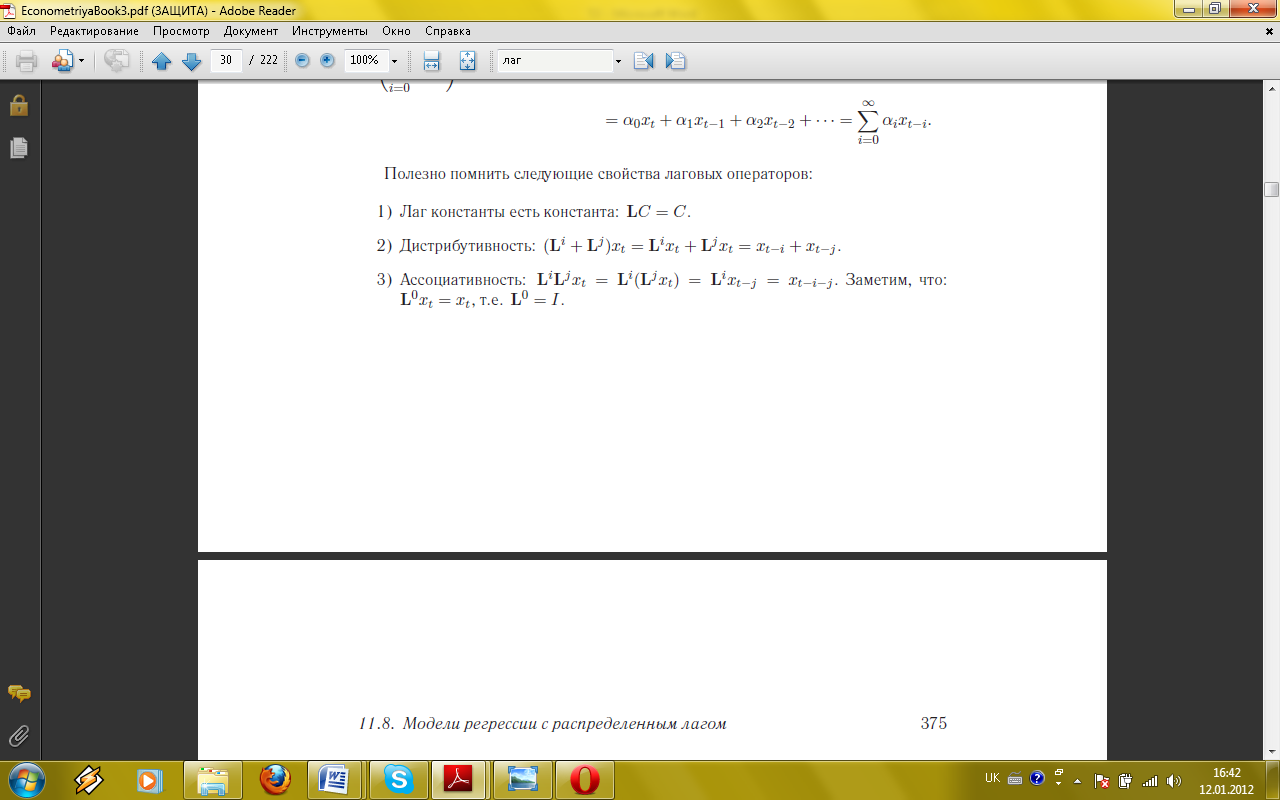
Відомі наступні властивості лагового оператору: 1) В С = С (лаг константи дорівнює константі) 2) Дистрибутивність:
3) Асоціативність: 4) Відємний лаг:
Міри точності прогнозів
Про точність прогнозу зазвичай судять за розміром помилки прогнозу - різниці між прогнозним і фактичним значенням досліджуваної змінної. Проте такий підхід до оцінювання точності можливий лише якщо дослідник має фактичні значення змінної. Отримані ретроспективно помилки прогнозу якоюсь мірою характеризують точність застосованої методики прогнозування і можуть виявитися корисними під час зіставляння кількох методів. Водночас розмір помилки ретроспективного прогнозу не можна розглядати як остаточний доказ придатності або, навпаки, непридатності застосовуваного методу прогнозування. Перевірка точності одного прогнозу мало що може сказати. Гарний одиничний прогноз можна отримати і за поганою моделлю, і навпаки. Звідси випливає, що про якість прогнозів застосовуваних методик і моделей можна судити лише за сукупністю зіставлень прогнозів і їхньої реалізації.
Найбільш простою мірою якості прогнозів за умови, що є дані про їхню реалізацію, може стати відношення кількості випадків, коли фактичну реалізацію охоплював інтервальний прогноз, до загальної кількості прогнозів, тобто
де т - кількість прогнозів, підтверджених фактичними даними; р - кількість прогнозів, не підтверджених фактичними даними. Коли всі прогнози підтверджуються, то р = 0 і Г) = 1; якщо ж усі прогнози не підтвердилися, то т, а отже, і г| дорівнюють 0. Міра якості прогнозу Г. Тейла: коефіцієнт розбіжності, чисельником якого є середньоквадратична похибка прогнозу, а знаменник дорівнює квадратному кореню із середнього квадрата реалізації, тобто
де р - кількість періодів, на які розраховують прогноз. Коефіцієнт V=0, коли всі уt prong= уt (випадок ідеального прогнозування); V = 1, коли процес прогнозування призводить до середньоквадратичної помилки "наївної" екстраполяції незмінності приростів; нарешті, V > 1, коли прогноз дає гірші результати, ніж припущення про незмінність досліджуваного явища. Верхньої межі коефіцієнт не має. Коефіцієнт розбіжності можна використати під час зіставляння якості прогнозів, одержаних на основі різноманітних методів і моделей. У цьому його безсумнівна привабливість. Також виокремлюють більш об'єктивні статистики точності прогнозів: МSЕ, RМSЕ, МАD, RМSPЕ, МАРЕ. Нехай yt_pr - прогноз значення часового ряду у t-му періоді, тоді:
- середня абсолютна похибка за р кроків
-
- за р кроків.
На практиці ці характеристики використовують досить часто. Перші три критерії виражають похибку в одиницях виміру, тому їхня величина залежить від специфіки часового ряду. Останні два критерії вимірюються у відносних одиницях, тому можна говорити про деякий загальний рівень адекватності моделі на основі їх порівняння.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.217.232 (0.012 с.) |




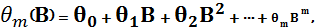
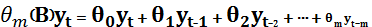


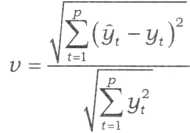
 Середньоквадратична похибка прогнозу за р кроків;
Середньоквадратична похибка прогнозу за р кроків; - корінь із середньокв-ї похибки
- корінь із середньокв-ї похибки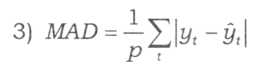
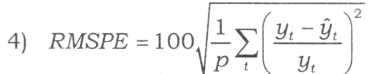 корінь із середньокв-ї похибки у відсотках від фактичних значень
корінь із середньокв-ї похибки у відсотках від фактичних значень середня абсолютна похибка у відсотках
середня абсолютна похибка у відсотках


