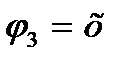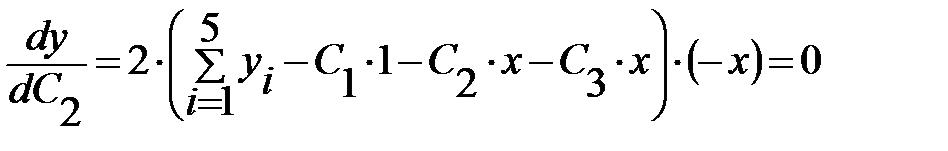Апроксимація функції методом найменших

КУРСОВА РОБОТА

З дисципліни “Обчислювальна техніка та програмування ” На тему:

АПРОКСИМАЦІЯ ФУНКЦІЇ МЕТОДОМ НАЙМЕНШИХ

КВАДРАТІВ

Студента І курсу групи КА-12-1 напряму підготовки 6.050902 Радіоелектронні апарати
Тарана А.А
Керівник доцент, канд. біол. наук Боцьва Н.П.
		Національна шкала Кількість балів Оцінка ECTS
Члени комісії:
__________________ ___________________________
	(підпис)	(прізвище та ініціали)
__________________ ___________________________
	(підпис)	(прізвище та ініціали)
__________________ ___________________________
	(підпис)	(прізвище та ініціали)

Зміст

Вступ……………..…………….………………………………………………………2

1 Метод найменших квадратів та його застосування для апроксимації функції

1.1 Означення методу…….…...……….………………………………………………2

1.2Методика вибору апроксимуючої функції ………………………………………3

2. Методика пошуку параметрів лінійної функції апроксимації…………………..5

2.1 Методика розв’язання нормальних рівнянь…………………..…………………5

2.2 Методика обчислення зворотньої матриці……………………………………...7

2. 3 Результати тестування програми………………………………………………..8

2.4 Складемо систему нормальних рівнянь …………………………………………8

2.5 Рішення систем методом зворотної матриці…………………………………….9

3.Програма знаходження параметрів лінійної функції апроксимації……......…..10

3.1Опис програми…………………………………………………………………….10

4.Результати машинного розрахунки………………………………………………15

Основні результати та висновки……………………………………………………16

Список використаної літератури…………………………………………………….17

 

 

Вступ

Під час вивчення залежностей між величинами важливим завданням є наближене представлення (апроксимація) цих залежностей за допомогою відомих функцій чи їх комбінацій, підібраних відповідно до задачі дослідження. Підхід до такого завдання і конкретний метод вирішення визначаються, вибором критерію якості наближення який використовується і формою подання вихідних даних.

У даній роботі розглянуто: метод найменших квадратів та його використання, методика вирішення нормальних рівнянь, алгоритм та сама програма.

Метод найменших квадратів та його застосування для апроксимації функції

Означення методу

Метод найменших квадратів(МНК)- один з методів регресійного аналізу для оцінки невідомих величин за результатами вимірів, що містять випадкові помилки.

Метод найменших квадратів застосовується також для наближеного представлення заданої функції іншими (простішими) функціями і часто виявляється корисним при обробці спостережень.

Коли бажана величина може бути виміряна безпосередньо, як, наприклад, довжина відрізка або кут, то, для збільшення точності, вимірювання проводиться багато разів, і за остаточний результат беруть арифметичне середнє з усіх окремих вимірювань. Це правило арифметичної середини грунтується на міркуваннях теорії ймовірностей; легко показати, що сума квадратів відхилень окремих вимірювань від арифметичної середини буде менше, ніж сума квадратів відхилень окремих вимірювань від якої б то не було іншої величини. Само правило арифметичної середини представляє, отже, найпростіший випадок методу найменших квадратів.

Апроксимація, або наближення – науковий метод, що складається в заміні одних об'єктів іншими, в тому чи іншому сенсі близькими до вихідних, але більш простими.

Апроксимація дозволяє досліджувати числові характеристики і якісні властивості об'єкта, зводячи завдання до вивчення більш простих або більш зручних об'єктів (наприклад, таких, характеристики яких легко обчислюються, або властивості яких вже відомі).

Методика пошуку параметрів лінійної функції апроксимації

Результати тестування програми

Припустимо, що зареєстровані експериментальні данні відображені у табл. 2

Табл.2

Xi	0,3	0,5	0,7	0,9	1,1
Yi	1,2	0,7	0,3	-0,3	-1,4

Складемо систему нормальних рівнянь

 

 

Рішення систем методом зворотної матриці

Результати розрахунку:

C₁=1,71; C₂=-1,552; C₃=-1,015;

Аппроксимуюча функція:

 

Програма знаходження параметрів лінійної функції апроксимації

Опис програми

#include<stdio.h>

#include<math.h>

#include<stdlib.h>

#define N 5 //максимальное количество точек;

#define K 2 //N-1 ////К-степень аппроксимирующего полинома

typedef float tArray[N];

typedef float tMatrix[N][N];

//a- массив коэффициентов полинома; b- массив свободных членов системы уравнений; x,y- координаты узловых точек;

tArray a, b;

tArray x, y;

//yt - массив y-координат, рассчитанных по найденному полиному; delta - массив разницы входных и рассчитанных y-значений;

tArray yt, delta;

tMatrix sums;

float Power(float v, int p);//возводит v в степень p;

void Calculate(); //вычисляет коэффициенты полинома

float Power(float v,int p)

{

if (p==0) return 1;

if (p>1) v *= Power(v, p-1);

return v;

}

void Perest()

{

int i, j;

float t;

//упорядочиваем узловые точки по возрастанию абсцисс

for(i = 0; i < N; i++)

for(j = i; j >= 1; j--)

if(x[j] < x[j-1])

{

t=x[j-1]; x[j-1]=x[j]; x[j]=t;

t=y[j-1]; y[j-1]=y[j]; y[j]=t;

}

}

 

void Calculate()

{

int i, j, k;

float s, M;

Perest(); //заполняем коэффициенты системы уравнений

for(i=0; i<K+1; i++)

{

for(j = 0; j < K + 1; j++)

{

sums[i][j] = 0;

for(k = 0; k < N; k++)

sums[i][j] += Power(x[k],i+j);

}

}

//заполняем столбец свободных членов

for(i=0; i<K+1; i++)

{

b[i] = 0;

for(k = 0; k < N; k++)

b[i] += Power(x[k],i) * y[k];

}

//применяем метод Гаусса для приведения матрицы системы к треугольному виду

for(k = 0; k < K + 1; k++)

{

for(i = k + 1; i < K + 1; i++)

{

M = sums[i][k] / sums[k][k];

for(j = k; j < K + 1; j++)

sums[i][j] -= M * sums[k][j];

b[i] -= M * b[k];

}

}

//вычисляем коэффициенты аппроксимирующего полинома

for(i = K; i >= 0; i--)

{

s=0;

for(j = i; j < K + 1; j++)

s += sums[i][j] * a[j];

a[i] = (b[i] - s) / sums[i][i];

}

}

void CalculateDelta()

{

int i, j;

float Y;

 

for (i = 0; i < N; i++)

{

Y = 0;

for(j = 0; j <= K; j++)

{

Y += a[j] * Power(x[i], j); //высчитываем значение полинома, заданного своими коэффициентами, в точке Х

}

yt[i] = Y;

delta[i] = y[i] - yt[i]; //вычисляем отклонение рассчитанной ординаты от входной

}

}

void inpArray(float *pArr)

{

int i;

for (i = 0; i < N; i++)

scanf("%f", &(pArr[i])); // Read a double from keyboard and assign to variable aFloat.

}

void outArray(float *pArr)

{

int i;

for (i = 0; i < N; i++)

printf(" %5.2f", pArr[i]);

printf("\n");

}

void outMatrix(tMatrix m)

{

int i;

for (i = 0; i < N; i++)

{

int j;

for (j = 0; j < N; j++)

printf(" %5.2f", m[i][j]);

printf("\n");

}

}

int main()

{

printf("vvedite znaceniya X\n");

inpArray(x);

printf("vvedite znaceniya Y\n");

inpArray(y);

printf("__________________________________________\n");

printf("kordunatu X: ");

outArray(x);

printf("kordunatu Y: ");

outArray(y);

printf("__________________________________________\n");

Calculate();

printf("Matritza sums \n");

outMatrix(sums);

printf(" Masuv koefitzientiv A\n");

outArray(a);

printf("Masuv svobodnuh chlenov B\n");

outArray(b);

CalculateDelta();

printf("Masuv naidenuh y - znachen: ");

outArray(yt);

printf(" Masuv znachen delta: ");

outArray(delta);

system("pause"); //это остановка программы до момента нажатия любой клавиши

return 0;

}

КУРСОВА РОБОТА

З дисципліни “Обчислювальна техніка та програмування ” На тему:

АПРОКСИМАЦІЯ ФУНКЦІЇ МЕТОДОМ НАЙМЕНШИХ

КВАДРАТІВ

Студента І курсу групи КА-12-1 напряму підготовки 6.050902 Радіоелектронні апарати
Тарана А.А
Керівник доцент, канд. біол. наук Боцьва Н.П.
		Національна шкала Кількість балів Оцінка ECTS
Члени комісії:
__________________ ___________________________
	(підпис)	(прізвище та ініціали)
__________________ ___________________________
	(підпис)	(прізвище та ініціали)
__________________ ___________________________
	(підпис)	(прізвище та ініціали)

Зміст

Вступ……………..…………….………………………………………………………2

1 Метод найменших квадратів та його застосування для апроксимації функції

1.1 Означення методу…….…...……….………………………………………………2

1.2Методика вибору апроксимуючої функції ………………………………………3

2. Методика пошуку параметрів лінійної функції апроксимації…………………..5

2.1 Методика розв’язання нормальних рівнянь…………………..…………………5

2.2 Методика обчислення зворотньої матриці……………………………………...7

2. 3 Результати тестування програми………………………………………………..8

2.4 Складемо систему нормальних рівнянь …………………………………………8

2.5 Рішення систем методом зворотної матриці…………………………………….9

3.Програма знаходження параметрів лінійної функції апроксимації……......…..10

3.1Опис програми…………………………………………………………………….10

4.Результати машинного розрахунки………………………………………………15

Основні результати та висновки……………………………………………………16

Список використаної літератури…………………………………………………….17

 

 

Вступ

Під час вивчення залежностей між величинами важливим завданням є наближене представлення (апроксимація) цих залежностей за допомогою відомих функцій чи їх комбінацій, підібраних відповідно до задачі дослідження. Підхід до такого завдання і конкретний метод вирішення визначаються, вибором критерію якості наближення який використовується і формою подання вихідних даних.

У даній роботі розглянуто: метод найменших квадратів та його використання, методика вирішення нормальних рівнянь, алгоритм та сама програма.