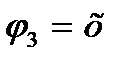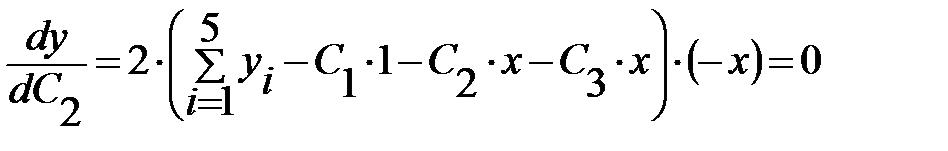Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика розв’язання нормальних рівняньСодержание книги
Поиск на нашем сайте Один з імовірних способів мінімізації критерію апроксимації (2) передбачає рішення системи нормальних рівнянь (3). При виборі як апроксимуючої функції лінійної функції шуканих параметрів нормальні рівняння можно розглядати як систему лінійних алгебраїчних рівнянь. Систему n лінійних рівнянь загального виду:
Формулу (4) можна записати у вигляді матричних позначень у наступному вигляді:А·Х=В, Квадратна матриця А називається матрицею системи, а вектори Х і У відповідно вектором-стовпцемневідомих системи і вектором-стовпцем її вільних членів.
(6)
Рішення системи лінійних рівнянь зводитися до відшукування значень елементів вектора-стовбця (хi),так званих коренями системи. Щоб ця система мала єдиний розв’язок, n рівняння яке входе в систему, має бути лінійно незалежним. Необхідна і достатня умова цього є нерівність нулю визначника системи, тобто Δ=detA≠0 Алгоритм розв’язання системи лінійних рівнянь підрозділяється на прямі та ітераціонні. На практиці ніякий метод не може бути нескінченним. Для отримання точного рішення ітераціонні методи вимагають нескінченне число арифметичних операцій. Практично це число ми змушені брати кінцевим і тому вирішення у принципі має деяку помилку, навіть якщо знехтувати помилками округлень, що супроводжують більшість обчислень. Що ж до прямих методів, вони навіть при кінцевому числі операцій можуть дати точне рішення, коли воно існує. Прямі і кінцеві методи дозволяють знайти рішення системи рівнянь за кінцеве число кроків. Таке рішення буде точним, якщо всі проміжки обчислення проводяться з обмеженою точністю. Методика обчислення зворотної матриці Один з методів рішення системи лінійних рівнянь (4), записуємо в матричній формі А·Х=В, пов'язаний із використанням зворотної матриці А-1. І тут рішення системи рівнянь виходить у такому вигляді Х=А-1·В, (7) де А-1 –матриця, обумовлена так. Нехай А –квадратна матриця розміром n x n с ненульовим визначником detA≠0. Тоді існує зворотна матриця R=A-1, обумовлена умовою A·R=E, де Е –одинична матриця, всф елементи головною діагоналі якої рівні I, а елементи поза цієї діагоналі -0,Е=[E1,..., En], де Еi –вектор-стовпець. Матриця К –квадратна матриця розміром n x n.
Де Розглянемо її перший стовпець R=(r11,r21,…,rn1)T, де Т –означає транспонування. Неважко перевірити, що A·R дорівнює першому стовпцю E1=(1, 0, …, 0)Т одиничної матриці Е, тобто. вектор R1 можна розгледіти як вирішення системи лінійних рівняньA·R1=E1. Аналогічно m –й стовпець матриці R, Rm, 1≤ m ≤ n, являє собою рішення рівняння A·Rm=Em, де Em=(0, …, 1, 0)T >m –й стовпець одиничної матриці E. Отже, зворотна матриця R-це набір із рішень n систем лінійних рівнянь A·Rm=Em, 1≤ m ≤ n. Аби вирішити ці системи можна використовувати будь-які методи, розроблені для вирішення алгебраїчних рівнянь. Проте метод Гаусса дає можливість вирішувати всі ці n рівнянь одночасно, а не незалежно одне від одного. Справді, всі ці системи рівнянь відрізняються лише правою частиною, проте усі перетворення, які проводяться у процесі прямого ходу методу Гаусса, повністю визначаються елементами матриці коефіцієнтів (матриці А). Отже, в схемах алгоритмів зміні підлягають лише блоки, пов'язані з перетворенням вектора В. У нашому випадку одночасно будуть змінюватися n векторів Em, 1≤ m ≤ n. Результатом рішення також буде чимало векторів, а n векторів Rm, 1≤ m ≤ n.
Результати тестування програми Припустимо, що зареєстровані експериментальні данні відображені у табл. 2 Табл.2
Складемо систему нормальних рівнянь
Рішення систем методом зворотної матриці
Результати розрахунку: C1=1,71; C2=-1,552; C3=-1,015; Аппроксимуюча функція:
Програма знаходження параметрів лінійної функції апроксимації Опис програми #include<stdio.h> #include<math.h> #include<stdlib.h> #define N 5 //максимальное количество точек; #define K 2 //N-1 ////К-степень аппроксимирующего полинома typedef float tArray[N]; typedef float tMatrix[N][N]; //a- массив коэффициентов полинома; b- массив свободных членов системы уравнений; x,y- координаты узловых точек; tArray a, b; tArray x, y; //yt - массив y-координат, рассчитанных по найденному полиному; delta - массив разницы входных и рассчитанных y-значений; tArray yt, delta; tMatrix sums; float Power(float v, int p);//возводит v в степень p; void Calculate(); //вычисляет коэффициенты полинома float Power(float v,int p) { if (p==0) return 1; if (p>1) v *= Power(v, p-1); return v; } void Perest() { int i, j; float t; //упорядочиваем узловые точки по возрастанию абсцисс for(i = 0; i < N; i++) for(j = i; j >= 1; j--) if(x[j] < x[j-1]) { t=x[j-1]; x[j-1]=x[j]; x[j]=t; t=y[j-1]; y[j-1]=y[j]; y[j]=t; } }
void Calculate() { int i, j, k; float s, M; Perest(); //заполняем коэффициенты системы уравнений for(i=0; i<K+1; i++) { for(j = 0; j < K + 1; j++) { sums[i][j] = 0; for(k = 0; k < N; k++) sums[i][j] += Power(x[k],i+j); } } //заполняем столбец свободных членов for(i=0; i<K+1; i++) { b[i] = 0; for(k = 0; k < N; k++) b[i] += Power(x[k],i) * y[k]; } //применяем метод Гаусса для приведения матрицы системы к треугольному виду for(k = 0; k < K + 1; k++) { for(i = k + 1; i < K + 1; i++) { M = sums[i][k] / sums[k][k]; for(j = k; j < K + 1; j++) sums[i][j] -= M * sums[k][j]; b[i] -= M * b[k]; } } //вычисляем коэффициенты аппроксимирующего полинома for(i = K; i >= 0; i--) { s=0; for(j = i; j < K + 1; j++) s += sums[i][j] * a[j]; a[i] = (b[i] - s) / sums[i][i]; } } void CalculateDelta() { int i, j; float Y;
for (i = 0; i < N; i++) { Y = 0; for(j = 0; j <= K; j++) { Y += a[j] * Power(x[i], j); //высчитываем значение полинома, заданного своими коэффициентами, в точке Х } yt[i] = Y; delta[i] = y[i] - yt[i]; //вычисляем отклонение рассчитанной ординаты от входной } } void inpArray(float *pArr) { int i; for (i = 0; i < N; i++) scanf("%f", &(pArr[i])); // Read a double from keyboard and assign to variable aFloat. } void outArray(float *pArr) { int i; for (i = 0; i < N; i++) printf(" %5.2f", pArr[i]); printf("\n"); } void outMatrix(tMatrix m) { int i; for (i = 0; i < N; i++) { int j; for (j = 0; j < N; j++) printf(" %5.2f", m[i][j]); printf("\n"); } } int main() { printf("vvedite znaceniya X\n"); inpArray(x); printf("vvedite znaceniya Y\n"); inpArray(y); printf("__________________________________________\n"); printf("kordunatu X: "); outArray(x); printf("kordunatu Y: "); outArray(y); printf("__________________________________________\n"); Calculate(); printf("Matritza sums \n"); outMatrix(sums); printf(" Masuv koefitzientiv A\n"); outArray(a); printf("Masuv svobodnuh chlenov B\n"); outArray(b); CalculateDelta(); printf("Masuv naidenuh y - znachen: "); outArray(yt); printf(" Masuv znachen delta: "); outArray(delta); system("pause"); //это остановка программы до момента нажатия любой клавиши return 0; }
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 373; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.007 с.) |

 (4)
(4) ;
;  ;
; 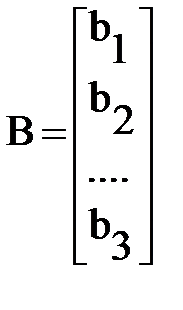 (5)
(5) У матричному вигляді вихідну систему n лінійних рівнянь можна записати й так:
У матричному вигляді вихідну систему n лінійних рівнянь можна записати й так: (8)
(8)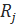 –вектор-стовпець.
–вектор-стовпець.