
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод зважених найменших квадратів (дисперсії відхилень невідомі)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Щоби використати метод зважених найменших квадратів, потрібно знати фактичні значення дисперсій випадкових величин at. На практиці такі значення відомі дуже рідко. Саме тому, щоби застосувати метод зважених найменших квадратів, потрібно зробити деякі припущення про значення
де Якщо встановлено наявність гетероскедастичності, потрібно трансформувати початкову модель таким чином, щоби випадкові помилки мали постійну дисперсію. Спосіб проведення трансформації початкової моделі залежить від форми залежності між дисперсією випадкових величин та значеннями факторних ознак:
На практиці розглядають кілька можливих перетворень: Випадок 1. Дисперсія У цьому разі припускаємо таку форму гетероскедастичності: де k2 —.коефіцієнт пропорційності, константа. Тоді трансформація моделі (2) полягає у діленні лівої і правої частин рівняння для кожного значення факторної ознаки xi на
Отже, для випадкових відхилень Справді, врахувавши умову (2), отримаємо:
Таким чином, під час оцінювання параметрів кореляційно-регресійної моделі (3) можна застосувати класичний метод найменших квадратів. Випадок 2. Дисперсія Розглянемо парну лінійну кореляційно-регресійну модель (4). Виражаючи коефіцієнт пропорційності, отримаєм
При цьому параметри регресії у кореляційно-регресійної моделі (5) помінялися місцями, тобто параметр регресії моделі (4) став вільним членом у моделі (5) і навпаки, вільний член моделі (4) став коефіцієнтом регресії при змінній 1/x. Випадкові величини vi мають властивість гомоскедастичності, оскільки
Таким чином, щоби знайти невідомі параметри кореляційно-регресійної моделі, можна використати метод найменших квадратів. Під час побудови множинної лінійної кореляційно-регресійної моделі можна діяти так само, як і під час першого припущення
Зауваження. Трансформовані змінні і трансформована кореляційно-регресійна модель можуть мати зовсім інший економічний зміст, ніж початкові змінні та модель. Алгоритм Феррара — Глобера. В алгоритмі Феррара — Глобера використовують три види статистичних критеріїв, на їхній підставі перевіряють мультиколінеарність: — критерій Алгоритм Феррара — Глобера складається з кількох кроків. Крок 1. Нормалізація факторних ознак x1,x2,..xk, яку здійснюють за допомогою перетворення Для нормалізованих значень факторних ознак виконуються умови: Елементами
де Якщо порівняти деякі кількісні значення часткових і парних коефіцієнтів кореляції, то можна побачити, що перші значно менші від других. Отже, на підставі лише часткових коефіцієнтів кореляції висновок про парну коліне-арність зробити неможливо. Для цього потрібно виконати ще сьомий крок. Крок 7. Розрахунок значень t- критерію — Аналізуючи значення критеріїв Fі t, можна зробити висновок, яку з факторних ознак потрібно вилучити з розгляду у побудованій кореляційно-регресійній моделі, це варто робити з огляду на економічні та логіко-теоретичні міркування. Якщо за допомогою алгоритму Феррара — Глобера не можна визначити, яку факторну ознаку потрібно вилучити з переліку змінних моделі, то оцінювати параметри моделі методом найменших квадратів не варто. У такому разі використовують інші методи, наприклад, метод головних компонент або одну з його модифікацій. 44. Узагальнений метод найменших квадратів (матричний підхід) На відміну від звичайного методу найменших квадратів, узагальнений метод найменших квадратів ураховує інформацію про неоднаковість дисперсії і тому дає можливість одержати найкращі лінійні оцінки. Розглянемо узагальнену множинну лінійну кореляційно-регресійну модель, зображену в матричному вигляді: це Y - це n-вимірна матриця-стовпець спостережень за результуючою змінною у; X - матриця спостережень розмірності п*(k + 1) за факторними ознаками х1,...,хk, у якій елементами першого стовпця є одиниці для одержання вільного члена моделі, а інші стовпці є векторами спостережень за факторними ознаками х1,...,хk; β – (k+1) - вимірна матриця-стовпець невідомих параметрів моделі; ε – n-вимірна матриця-стовпець випадкових величин εі.
Вибіркова кореляційно-регресійна модель має вигляд:
Позначимо через е = Y-Ỹ вектор випадкових відхилень. Завдання полягає у знаходженні оцінок елементів вектора β у моделі. Для цього використовують матрицю S, за допомогою якої коригують вхідну інформацію. Оскільки S — додатно визначена матриця, то вона може бути представлена як добуток РРТ, де матриця Р є ненародженою, тобто S = РРТ. При заданій матриці S оцінки параметрів моделі можна обчислити за формулою
Дисперсія трансформованої похибки ε є постійною величиною, тобто для моделі P-1Y=P-1Xβ+P-1ε виконується припущення про гомоскедастичність і оцінювання її параметрів можна проводити на підставі методу найменших квадратів.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 567; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.116.231 (0.012 с.) |

 .Розгляньмо парну лінійну кореляційно-регресійну модель (1)
.Розгляньмо парну лінійну кореляційно-регресійну модель (1)
 — випадкова величина, яка є гетероскедастичною, але відповідає всім іншим припущенням кореляційно-регресійного аналізу.
— випадкова величина, яка є гетероскедастичною, але відповідає всім іншим припущенням кореляційно-регресійного аналізу.
 пропорційна xi.
пропорційна xi. (2)
(2) :
:
 виконується умова гомоскедастичності.
виконується умова гомоскедастичності.
 Припустімо, що форма гетероскедастичності має вигляд
Припустімо, що форма гетероскедастичності має вигляд 
 . Це означає,що трансформація початкової моделі полягає у діленні моделі на хi-. Трансформована кореляційно-регресійна модель має вигляд:
. Це означає,що трансформація початкової моделі полягає у діленні моделі на хi-. Трансформована кореляційно-регресійна модель має вигляд: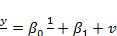 (4)
(4)
 тобто досліджувати залежність дисперсії
тобто досліджувати залежність дисперсії  вибіркової множинної лінійної кореляційно-регресійної моделі.
вибіркової множинної лінійної кореляційно-регресійної моделі. , за допомогою якого перевіряють мультиколінеарність усього масиву факторних ознак; — F -критерій, за його допомогою перевіряють гіпотезу Н0: коефіцієнт детермінації
, за допомогою якого перевіряють мультиколінеарність усього масиву факторних ознак; — F -критерій, за його допомогою перевіряють гіпотезу Н0: коефіцієнт детермінації  дорівнює нулю:
дорівнює нулю:  та гіпотезу H1:коефіцієнт детермінації
та гіпотезу H1:коефіцієнт детермінації  не дорівнює нулю:
не дорівнює нулю: 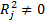 . За допомогою F- тесту перевіряють кореляцію кожної факторної ознаки з усіма іншими; — Т -критерій, на підставі якого перевіряють гіпотезу Н0: частковий коефіцієнт кореляції дорівнює нулю:
. За допомогою F- тесту перевіряють кореляцію кожної факторної ознаки з усіма іншими; — Т -критерій, на підставі якого перевіряють гіпотезу Н0: частковий коефіцієнт кореляції дорівнює нулю: 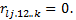 та гіпотезу Н1: частковий коефіцієнт кореляції не дорівнює нулю:
та гіпотезу Н1: частковий коефіцієнт кореляції не дорівнює нулю:  де
де  — часткові коефіцієнти кореляції, які характеризують тісноту зв'язку між факторними ознаками хl та хj за умови, що решта факторних ознак не впливає на цей зв'язок. За допомогою t- тесту перевіряють наявність лінійної кореляційної залежності кожної пари факторних ознак. Порівняння розрахованих значень цих критеріїв з їхніми критичними значеннями дає можливість зробити висновки щодо наявності чи відсутності мультиколінеарності.
— часткові коефіцієнти кореляції, які характеризують тісноту зв'язку між факторними ознаками хl та хj за умови, що решта факторних ознак не впливає на цей зв'язок. За допомогою t- тесту перевіряють наявність лінійної кореляційної залежності кожної пари факторних ознак. Порівняння розрахованих значень цих критеріїв з їхніми критичними значеннями дає можливість зробити висновки щодо наявності чи відсутності мультиколінеарності. , (7.78) де п — величина вибірки для кожної змінної (i=1,n); k- кількість факторних ознак у моделі (j=1,k);
, (7.78) де п — величина вибірки для кожної змінної (i=1,n); k- кількість факторних ознак у моделі (j=1,k);  — середнє значення j- ї факторної ознаки;
— середнє значення j- ї факторної ознаки;  — дисперсія j -ї факторної ознаки.
— дисперсія j -ї факторної ознаки. Крок 2. Обчислення кореляційної матриці
Крок 2. Обчислення кореляційної матриці  де X* — матриця нормалізованих значень факторних ознак.
де X* — матриця нормалізованих значень факторних ознак. матриці R є парні коефіцієнти кореляції, які характеризують тісноту зв'язку між l-ю та j-ю факторними ознаками. Однак на підставі знайденої кореляційної матриці В не можна стверджувати, що отриманий зв'язок є явищем мультиколінеарності. Крок 3. Обчислення значення
матриці R є парні коефіцієнти кореляції, які характеризують тісноту зв'язку між l-ю та j-ю факторними ознаками. Однак на підставі знайденої кореляційної матриці В не можна стверджувати, що отриманий зв'язок є явищем мультиколінеарності. Крок 3. Обчислення значення  -критерію —
-критерію — 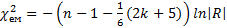 , де
, де  — визначник кореляційної матриці R. Знаходимо табличне значення
— визначник кореляційної матриці R. Знаходимо табличне значення  при —
при —  ступенях вільності і рівні значущості α. Якщо
ступенях вільності і рівні значущості α. Якщо 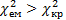 , тоімовірністю р=1-α можна стверджувати, що в масиві факторних ознак є мультиколінеарність. Якщо
, тоімовірністю р=1-α можна стверджувати, що в масиві факторних ознак є мультиколінеарність. Якщо  , то з імовірністю р=1-α можемо зробити висновок щодо відсутності мультиколінеарності. Крок 4. Визначення матриці помилок С=
, то з імовірністю р=1-α можемо зробити висновок щодо відсутності мультиколінеарності. Крок 4. Визначення матриці помилок С=  . Крок 5. Розрахунок значень F- критерію —
. Крок 5. Розрахунок значень F- критерію —  де
де  -діагональні елементи матриці С. При заданих ступенях вільності n-k і k-1 та рівні значущості α знаходимо табличне значення критерію і порівнюємо розраховані значення
-діагональні елементи матриці С. При заданих ступенях вільності n-k і k-1 та рівні значущості α знаходимо табличне значення критерію і порівнюємо розраховані значення  з табличним
з табличним  . Якщо
. Якщо 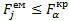 , то з імовірністю р=1-α гіпотезу Н0 приймаємо, тобто факторна ознака хj не є колінеарною з усіма іншими. На підставі діагональних елементів матриці С можна розрахувати коефіцієнти детермінації для кожної факторної ознаки:
, то з імовірністю р=1-α гіпотезу Н0 приймаємо, тобто факторна ознака хj не є колінеарною з усіма іншими. На підставі діагональних елементів матриці С можна розрахувати коефіцієнти детермінації для кожної факторної ознаки: 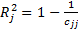 . Коефіцієнт детермінації
. Коефіцієнт детермінації 
 — елемент матриці С, який розміщений на перетині l-ї стрічки та j- го стовпця;
— елемент матриці С, який розміщений на перетині l-ї стрічки та j- го стовпця;  діагональні елементи матриці С.
діагональні елементи матриці С.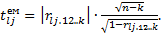 Розраховані значення критерію
Розраховані значення критерію 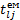 порівнюємо з табличним значенням
порівнюємо з табличним значенням  при n-k ступенях вільності і рівні значущості α. Якщо
при n-k ступенях вільності і рівні значущості α. Якщо  то з імовірністю р=1-α гіпотезу Н0 відкидаємо, тобто між факторними ознаками x l і хj наявна колінеарність. Якщо
то з імовірністю р=1-α гіпотезу Н0 відкидаємо, тобто між факторними ознаками x l і хj наявна колінеарність. Якщо 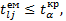 то з імовірністю р=1-α гіпотезу Н0 приймаємо, тобто факторні ознаки хl і хj неколінеарні.
то з імовірністю р=1-α гіпотезу Н0 приймаємо, тобто факторні ознаки хl і хj неколінеарні.
 де Ỹ- n-вимірна матриця-стовпець теоретичних значень результуючої змінної, що розраховані на підставі кореляційно-регресійної моделі; b – (k+1) – вимірна матриця-стовпець оцінок параметрів кореляційно-регресійної моделі.
де Ỹ- n-вимірна матриця-стовпець теоретичних значень результуючої змінної, що розраховані на підставі кореляційно-регресійної моделі; b – (k+1) – вимірна матриця-стовпець оцінок параметрів кореляційно-регресійної моделі.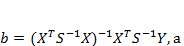 стандартну похибку — згідно
стандартну похибку — згідно  . Отже, ми можемо побудувати довірчі інтервали та критерії перевіряння статистичної значущості параметрів регресії β.
. Отже, ми можемо побудувати довірчі інтервали та критерії перевіряння статистичної значущості параметрів регресії β.


