
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тестування автокореляції. Критерій Дарбіна-Уотсона (DW-критерій)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для тестування автокореляції 1-го порядку між сусідніми значеннями відхилень використовують критерій Дарбіна - Уотсона, який обчислюють за допомогою формули:
При заданому рівні значущості α, кількості спостережень Т та факторів k визначають критичні значення Після цього будують так звані зони кореляційного зв’язку:
0
\\\\\\\\\\ - невизначеність. Якщо емпіричне значення статистики попадає в дану невизначеність, то для тестування наявності чи відсутності автокореляції необхідно змінити рівень значущості α. В деяких випадках для тестування автокореляції використовують коефіцієнт кореляції між сусідніми значеннями випадкових відхилень
При достатньо великих значеннях T, величини
Покажемо наявність залежності чи зв’язку між коефіцієнтами Д-У і коефіцієнта автокореляції 1-го порядку:
Тоді коефіцієнт Д-У можна представити:
Р-ня (2) можна виразити
Тестування наявності автокореляції за допомогою критерію Д-У можливе в таких випадках: 1) Кр. Д-У використовується тільки для тих моделей, які містять вільний член 2) Припускають, що випадкові величини
Модель (3) наз. Авто регресійною моделю Маркова 1-го порядку 3) статистичні дані повинні мати однакову періодичність; 4) Кр. Д-У не застосовують для визначення автокореляції у авто регресійних моделях. Тестування автокореляції. h-критерій Дарбіна-Уотсона h-критерій Дарбіна-Уотсона використовують, щоби виявити автокореляцію в авто регресійних моделях. Аби протестувати автокореляцію, сформуємо нульову гіпотезу Щоби перевірити гіпотезу про статистичну значущість коефіцієнта автокореляції, використовуємо h-статистику Д-У, яку визначають за формулою
де Якщо обсяг вибірки великий, h-статистика має нормований нормальний розподіл з математичним сподіванням, що дорівнює нулю: E( Якщо Якщо Основною проблемою при використанні цього тесту є неможливість обчислити значення Зауваження. Значення
а
Метод Кохрана-Оркатта Одним з можливих методів оцінювання коефіцієнта автокореляції ρ є ітеративний процес, який називають методом Кохрана-Оркатта. Його можна описати на прикладі ПЛКРМ:
Метод Кохрана-Оркатта складається з таких етапів: 1. За допомогою МНК (методу найменших квадратів) знаходять оцінки параметрів заданої кореляційно-регресійної моделі. 2. На підставі вибіркової кореляційно-регресійної моделі обчислюють значення випадкових відхилень 3. Використовуючи модель AR(1) (авто регресійна модель Маркова першого порядку
4. На підставі цієї моделі будують кореляційно-регресійну модель:
5. Оцінки Процес оцінювання параметра ρ триває доти, доки не буде досягнута потрібна точність, тобто поки різниця між попереднім та поточним значеннями оцінки
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 517; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.54.188 (0.008 с.) |


 ,
,  за таблицями розподілу Д-У.
за таблицями розподілу Д-У.

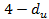
 4
4 - автокореляція відсутня;
- автокореляція відсутня; - від’ємна автокореляція;
- від’ємна автокореляція; - додатня автокореляція;
- додатня автокореляція; ,
,  , який називається коефіцієнт 1-го порядку:
, який називається коефіцієнт 1-го порядку: (1)
(1) , тоді формулу (1) можна записати у вигляді:
, тоді формулу (1) можна записати у вигляді:

 ,
, ;
;  (2)
(2)
 – додатня автокореляція
– додатня автокореляція - відємна автокореляція
- відємна автокореляція ;
; визначають за такою ітераційною схемою
визначають за такою ітераційною схемою 
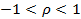 , (3)
, (3)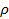 - коефіцієнт автокореляції;
- коефіцієнт автокореляції; - вип. вел. для якої виконуються всі припущення класичного кор.-рег. аналізу.
- вип. вел. для якої виконуються всі припущення класичного кор.-рег. аналізу. : коефіцієнт автокореляції першого порядку дорівнює нулю
: коефіцієнт автокореляції першого порядку дорівнює нулю  .
.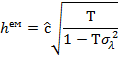
 - оцінка коефіцієнта
- оцінка коефіцієнта  -вибіркова дисперсія коефіцієнта регресії при лаговій змінній
-вибіркова дисперсія коефіцієнта регресії при лаговій змінній  ; T-кількість спостережень.
; T-кількість спостережень. та дисперсією, що дорівнює одиниці:
та дисперсією, що дорівнює одиниці:  =1. Тому при заданому рівні значущості
=1. Тому при заданому рівні значущості  визначають критичну точку
визначають критичну точку  з умови
з умови 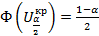 (Ф(u)-функція Лапласа) і порівнюють розраховане значення
(Ф(u)-функція Лапласа) і порівнюють розраховане значення  з табличним
з табличним  , то нульову гіпотезу
, то нульову гіпотезу  , то нульову гіпотезу
, то нульову гіпотезу 

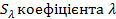 при лаговій результуючій змінній. Тому значення h-критерію можна обчислити на підставі даних вибіркової кореляційно-регресійної моделі.
при лаговій результуючій змінній. Тому значення h-критерію можна обчислити на підставі даних вибіркової кореляційно-регресійної моделі.
 .
.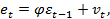
 ), знаходять оцінку
), знаходять оцінку 
 ,
,
 .
. параметрів
параметрів  коефіцієнта автокореляції ρ не стане меншою від наперед заданого числа (величини заданої похибки).
коефіцієнта автокореляції ρ не стане меншою від наперед заданого числа (величини заданої похибки).


