
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття застосування симультативних моделей. Модель попиту на товар.Содержание книги
Поиск на нашем сайте
Поняття застосування симультативних моделей. Модель попиту на товар. В економічній теорії оперують кількома видами попиту: макроекономіка- сукупний попит, мікроекономіка- ринковий попит. Індивідуальний попит, попит на продукт окремої фірми. Припустимо, що нам треба оцінити ринкову величину попиту на деякий товар. З економічної теорії відомо, що попит на будь-який товар залежить від цінових та нецінових чинників (детермінантів). Ціновий чинник- це власне ціна товару P. До найважливіших нецінови детермінантів належить: - Ціни споріднених товарів - P0; - Доходи споживачів-y; - Смаки та вподобання споживачів - W; - Чисельність населення та його структура – N; - Очікування споживач. Стосовно майбутніх доходів та цін – М; - Специфічні чинники – S. Таким чином обся попиту на товар можна представити у вигляді багатофакторної регресійної моделі: Q=f(P, P0, y, W, M, N, S, Z), де Z – інші чинники. Припустимо, що математико-статистичний аналіз факторів, що впливають на обсяг попиту на певний товар, показує, що найбільш статистично значними є такі фактори: власна ціна товару, ціни споріднених товарів, доходи споживачів. Припустимо також, що залежність між обсягом попиту на товар і цими факторами є лінійною. Тоді функцію попиту на товар можна записати у вигляді: , де Проте в моделі (1) існує двосторонній зв'язок, внаслідок чого порушується 4 припущення регресійного аналізу і використання МНК дасть зміщені оцінки параметрів зв’язку. Саме тому рівняння (1) не можна розглядати як повну модель попиту на това. До цього рівняння треба приєднати принаймні ще одне рівняння, яке описує зв'язок між P та Q, наприклад, V - випадкова величина, а S – специфічний чинник. Рівняння (1),(2) утворюють систему симультативних рівнянь, яка є економетричною моделлю попиту. Покажемо що у рівнянні (1) змінна Р залежить від випадкової величини.підставивши в р-ня (2) вираз для Q (1)отримаємо:
рівняння (3) показує, що змінна Р залежить від випадкової величини
Поняття застосування симультативних моделей. Модель грошової пропозиції. Пропозиція грошей – це кількість грошей, яка наявна в національній економіці на деякий момент часу. Пропозиція грошей є одним із знарядь проведення макроекономічної політики, регулювання пропозиції грошей називають монетарною політикою. Її суть полягую в контролюванні Національним банком пропозиції грошей, відсоткових ставок, ринків капіталу. Припустимо, що нам треба оцінити пропозицію грошей. Одним з основних детермінантів монетарної політики є національний дохід. У зв’язку з цим функцію грошової пропозиції можна записати як парну лінійну кореляційно-регресійну модель
Підставивши (1) в (2), отримаємо:
Визначення r на основі статистики Дарбіна-Уотсона Критерій Д-У тісно пов'язаний із коеф.кореляції між сусідніми відхиленнями
Тоді оцінка Цей метод оцінювання коеф.автокореляції r застосовують при великій кількості спостережень. У цьому разі оцінка
Метод Хілдрета-Лу За цим методом КРМ Недоліком цього методу є потреба побудови достатньо великої к-ті КРМ та оцінювання їх якості (знаходження стандартної похибки моделі або значення коефіцієнта детермінації). Ітераційний метод Х.-Лу зазвичай використовують в економетричних пакетах.
Цей метод використовують тоді, коли є вважають, що автокореляція випадкових величин достатньо велика, тобто його використовують тільки для двох значень параметра r: r=1 та r=-1. Для динамічних рядів характерна додатна автокореляція випадкових відхилень
можна сформулювати так:
Якщо позначити через
Оцінку
Коли r=-1, то маємо таку КРМ: Або Зробивши заміну змінних
Зміна специфікації моделі Інколи проблему мультиколінеарності можна вирішити зміною специфікації моделі: або зміною форми моделі, або додаванням факторних змінних, що не враховані в початковій моделі, однак помітно впливають на результуючу змінну. Якщо цей підхід обґрунтований, то його використання зменшує суму квадратів випадкових відхилень, що зменшує стандартну похибку моделі, а отже, і знижує стандартну похибку коефіцієнтів регресії. Перетворення змінних Інколи мінімізувати або взагалі усунути проблему мультиколінеарності можна за допомогою перетворення змінних. Однією із причин мультиколінеарності факторних ознак є їхня схильність змінюватись в одному напрямку. Зменшення такої залежності здійснюється за допомогою використання у кореляційно-регресійній моделі перших різниць послідовних у часі факторних ознак:
Цей прийом здебільшого зменшує мільтиколінеарність, оскільки різниці факторних ознак не завжди високо колінеарні. Але такі перетворення породжують додаткові проблеми. Випадкова величина Модель Койка Роблять 2 припущення: 1) Коефіцієнти Параметр Враховуючи припущення (1) нескінченно ДЛМ можна записати у вигляді: Модель (2) з запізненням в 1 період Модель (3) домножимо на Від моделі (2) віднімемо модель (4)
Має такі особливості: 1) у ДЛМ ми отримуємо авто-регресійну модель; 2) під час оцінювання моделі (5) необхідно перевірити чи змінна Переваги: 1) чітке припущення що всі 27. Модель адаптивних очікувань (перша модель модифікації Койка) Підхід Койка до дистрибутивно-лагових моделей Койк запропонував досить цікавий метод оцінки дистрибутивно-лагових моделей. Припустимо, ми починаємо з дистрибутивно-лагової моделі з невизначеним лaгом ( - припускаючи, що λ можуть бути від'ємними, Койк абстрагувався від зміни знака коефіцієнта при βі; - завдяки тому, що λ<1 віддалені за часом, значення βі стали менш впливовими, ніж поточні; - сума βі, яка складає довгостроковий мультиплікатор, є скінченною, тобто . як результат (1.4), модель з кінцевим лагом (1.5) можна записати таким чином: .
28. Модель часткових пристусувань(друга МОДИФІКАЦІЇ моделі Койка) Як бачимо, модель (1.6) також незручна для оцінки, оскільки залишається дуже велика (фактично нескінченна) кількість оцінюваних параметрів, крім того, параметр λ входить до моделі в нелінійній формі: тобто метод лінійної (за параметрами) регресії не можна застосувати до цієї моделі. Але Койк пропонує модифікований метод, який полягає в тому, що в модель (1.6) вводиться затримка на один період. Виходячи з цього, модель записується таким чином:
Далі помножуємо (1.7) на λ і отримаємо:
Віднявши (1.8) від (1.6), маємо:
де Зазначимо деякі особливості трансформації Койка. 1. Трансформація Койка переводить дистрибутивно-лагову модель в авторегресивну, оскільки серед незалежних змінних залишається уt-1. 2. Поява уt-1 може спричинити ряд статистичних проблем: уt-1, як і уt, - стохастична; це означає, що в модель ми вводимо стохастичну змінну. 3. У початковій моделі (1.3) помилка дорівнювала εt, а в перетвореній 4. Наявність лагового значення у порушує одне з припущень d-тесту Дарбіна-Уотсона. Отже, нам потрібно розробити альтернативу для тестування серійної кореляції при лаговому у. Цією альтернативою є h-тест Дарбіна. Метод Кохрана-Оркатта Одним з можливих методів оцінювання коефіцієнта автокореляції ρ є ітеративний процес, який називають методом Кохрана-Оркатта. Його можна описати на прикладі ПЛКРМ:
Метод Кохрана-Оркатта складається з таких етапів: 1. За допомогою МНК (методу найменших квадратів) знаходять оцінки параметрів заданої кореляційно-регресійної моделі. 2. На підставі вибіркової кореляційно-регресійної моделі обчислюють значення випадкових відхилень 3. Використовуючи модель AR(1) (авто регресійна модель Маркова першого порядку
4. На підставі цієї моделі будують кореляційно-регресійну модель:
5. Оцінки Процес оцінювання параметра ρ триває доти, доки не буде досягнута потрібна точність, тобто поки різниця між попереднім та поточним значеннями оцінки
Алгоритм Феррара — Глобера. В алгоритмі Феррара — Глобера використовують три види статистичних критеріїв, на їхній підставі перевіряють мультиколінеарність: — критерій Алгоритм Феррара — Глобера складається з кількох кроків. Крок 1. Нормалізація факторних ознак x1,x2,..xk, яку здійснюють за допомогою перетворення Для нормалізованих значень факторних ознак виконуються умови: Елементами де Якщо порівняти деякі кількісні значення часткових і парних коефіцієнтів кореляції, то можна побачити, що перші значно менші від других. Отже, на підставі лише часткових коефіцієнтів кореляції висновок про парну коліне-арність зробити неможливо. Для цього потрібно виконати ще сьомий крок. Крок 7. Розрахунок значень t- критерію — Аналізуючи значення критеріїв Fі t, можна зробити висновок, яку з факторних ознак потрібно вилучити з розгляду у побудованій кореляційно-регресійній моделі, це варто робити з огляду на економічні та логіко-теоретичні міркування. Якщо за допомогою алгоритму Феррара — Глобера не можна визначити, яку факторну ознаку потрібно вилучити з переліку змінних моделі, то оцінювати параметри моделі методом найменших квадратів не варто. У такому разі використовують інші методи, наприклад, метод головних компонент або одну з його модифікацій. 44. Узагальнений метод найменших квадратів (матричний підхід) На відміну від звичайного методу найменших квадратів, узагальнений метод найменших квадратів ураховує інформацію про неоднаковість дисперсії і тому дає можливість одержати найкращі лінійні оцінки. Розглянемо узагальнену множинну лінійну кореляційно-регресійну модель, зображену в матричному вигляді: це Y - це n-вимірна матриця-стовпець спостережень за результуючою змінною у; X - матриця спостережень розмірності п*(k + 1) за факторними ознаками х1,...,хk, у якій елементами першого стовпця є одиниці для одержання вільного члена моделі, а інші стовпці є векторами спостережень за факторними ознаками х1,...,хk; β – (k+1) - вимірна матриця-стовпець невідомих параметрів моделі; ε – n-вимірна матриця-стовпець випадкових величин εі. Вибіркова кореляційно-регресійна модель має вигляд:
Позначимо через е = Y-Ỹ вектор випадкових відхилень. Завдання полягає у знаходженні оцінок елементів вектора β у моделі. Для цього використовують матрицю S, за допомогою якої коригують вхідну інформацію. Оскільки S — додатно визначена матриця, то вона може бути представлена як добуток РРТ, де матриця Р є ненародженою, тобто S = РРТ. При заданій матриці S оцінки параметрів моделі можна обчислити за формулою
Дисперсія трансформованої похибки ε є постійною величиною, тобто для моделі P-1Y=P-1Xβ+P-1ε виконується припущення про гомоскедастичність і оцінювання її параметрів можна проводити на підставі методу найменших квадратів.
Поняття застосування симультативних моделей. Модель попиту на товар. В економічній теорії оперують кількома видами попиту: макроекономіка- сукупний попит, мікроекономіка- ринковий попит. Індивідуальний попит, попит на продукт окремої фірми. Припустимо, що нам треба оцінити ринкову величину попиту на деякий товар. З економічної теорії відомо, що попит на будь-який товар залежить від цінових та нецінових чинників (детермінантів). Ціновий чинник- це власне ціна товару P. До найважливіших нецінови детермінантів належить: - Ціни споріднених товарів - P0; - Доходи споживачів-y; - Смаки та вподобання споживачів - W; - Чисельність населення та його структура – N; - Очікування споживач. Стосовно майбутніх доходів та цін – М; - Специфічні чинники – S. Таким чином обся попиту на товар можна представити у вигляді багатофакторної регресійної моделі: Q=f(P, P0, y, W, M, N, S, Z), де Z – інші чинники. Припустимо, що математико-статистичний аналіз факторів, що впливають на обсяг попиту на певний товар, показує, що найбільш статистично значними є такі фактори: власна ціна товару, ціни споріднених товарів, доходи споживачів. Припустимо також, що залежність між обсягом попиту на товар і цими факторами є лінійною. Тоді функцію попиту на товар можна записати у вигляді: , де Проте в моделі (1) існує двосторонній зв'язок, внаслідок чого порушується 4 припущення регресійного аналізу і використання МНК дасть зміщені оцінки параметрів зв’язку. Саме тому рівняння (1) не можна розглядати як повну модель попиту на това. До цього рівняння треба приєднати принаймні ще одне рівняння, яке описує зв'язок між P та Q, наприклад, V - випадкова величина, а S – специфічний чинник. Рівняння (1),(2) утворюють систему симультативних рівнянь, яка є економетричною моделлю попиту. Покажемо що у рівнянні (1) змінна Р залежить від випадкової величини.підставивши в р-ня (2) вираз для Q (1)отримаємо:
рівняння (3) показує, що змінна Р залежить від випадкової величини
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.148.76 (0.012 с.) |

 (1)
(1) - невідомі параметри багатофакторної регресійної моделі, а
- невідомі параметри багатофакторної регресійної моделі, а 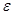 - випадкова величина.
- випадкова величина.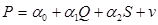 (2), де
(2), де  - невідомі параметри рівняння;
- невідомі параметри рівняння;

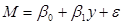 (1), де М – грошова пропозиція; у – національний дохід;
(1), де М – грошова пропозиція; у – національний дохід;  - невідомі параметри моделі; а
- невідомі параметри моделі; а  (2) де І – інвестиційні видатки.
(2) де І – інвестиційні видатки.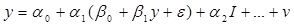 тобто ендогенна змінна у р-ння (1) залежить від вип.. величини Е:
тобто ендогенна змінна у р-ння (1) залежить від вип.. величини Е:  .
. співвідношенням:
співвідношенням: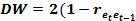 )
) коефіцієнта автокореляції r може дорівнювати
коефіцієнта автокореляції r може дорівнювати  , тобто:
, тобто: 
 (1) оцінюють для кожного можливого значення r з інтервалу [-1;1] з деяким заданим кроком (напр.,0,001; 0,01 тощо). Величину
(1) оцінюють для кожного можливого значення r з інтервалу [-1;1] з деяким заданим кроком (напр.,0,001; 0,01 тощо). Величину  і
і  оцінюють з корел-регр.моделі (1) саме із цим значенням r.
оцінюють з корел-регр.моделі (1) саме із цим значенням r. або
або 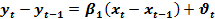 (2)
(2) , то залежність (2) можна записати так:
, то залежність (2) можна записати так: (3)
(3)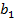 параметра
параметра  параметра
параметра  не визначають безпосередньо з КРМ, а обчислюють за формулою:
не визначають безпосередньо з КРМ, а обчислюють за формулою: .
.
 (4)
(4)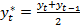 ,
,  , маємо таку ПЛКРМ:
, маємо таку ПЛКРМ:

 може не задовольняти припущення класичного кореляційно-регресійного аналізу, зокрема, виникнення автокореляції випадкової величини. Використання перших різниць призводить до зменшення ступенів вільності на 1, що суттєво впливає на результати у малих вибірках.
може не задовольняти припущення класичного кореляційно-регресійного аналізу, зокрема, виникнення автокореляції випадкової величини. Використання перших різниць призводить до зменшення ступенів вільності на 1, що суттєво впливає на результати у малих вибірках. мають одинаковий знак; 2) Коефіцієнти
мають одинаковий знак; 2) Коефіцієнти 
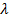 наз. темп зростання ДЛ, а
наз. темп зростання ДЛ, а  швидкість прискорювання
швидкість прискорювання


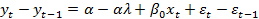
 для оцінювання параметрів моделі (5) можна застосувати МНК
для оцінювання параметрів моделі (5) можна застосувати МНК є не стохастична, тобто чи не зал. від випадкової величини
є не стохастична, тобто чи не зал. від випадкової величини 
 і змін в геометричній прогресії; 2) мат. модель.
і змін в геометричній прогресії; 2) мат. модель. =
=  ). Припускаючи, що βі мають той самий знак, Койк припустив також, що вони змінюються в геометричній прогресії:
). Припускаючи, що βі мають той самий знак, Койк припустив також, що вони змінюються в геометричній прогресії: 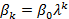 k = 0, 1, …, (1.4) де λ такі, що 0 < λ < 1 – темп зменшення дистрибутивного лагу, а (1- λ) – швидкість пристосування. Співвідношення (1.4) показує, що кожний наступний коефіцієнт β менший, ніж попередній (оскільки λ< 1), тобто з кожним наступним кроком у минуле вплив лaгу на уt поступово зменшується, що є досить імовірним припущенням. Значення лaгового коефіцієнта βк -залежить, крім загального β0 також і від λ. Чим ближче значення λ до 1, тим повільніший темп зменшення βк, а чим ближче він до 0, тим швидше спадає βк. У попередньому випадку віддалені в минулому значення х досить сильно впливали на уt, тоді як у нашому випадку їхній вплив на уt швидко зменшується. Слід зазначити, що метод Койка має такі переваги:
k = 0, 1, …, (1.4) де λ такі, що 0 < λ < 1 – темп зменшення дистрибутивного лагу, а (1- λ) – швидкість пристосування. Співвідношення (1.4) показує, що кожний наступний коефіцієнт β менший, ніж попередній (оскільки λ< 1), тобто з кожним наступним кроком у минуле вплив лaгу на уt поступово зменшується, що є досить імовірним припущенням. Значення лaгового коефіцієнта βк -залежить, крім загального β0 також і від λ. Чим ближче значення λ до 1, тим повільніший темп зменшення βк, а чим ближче він до 0, тим швидше спадає βк. У попередньому випадку віддалені в минулому значення х досить сильно впливали на уt, тоді як у нашому випадку їхній вплив на уt швидко зменшується. Слід зазначити, що метод Койка має такі переваги: (1.5)
(1.5) (1.6)
(1.6)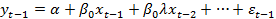 (1.7)
(1.7) (1.8)
(1.8) (1.10)
(1.10) . Ця процедура відома як перетворення Койка. Порівнюючи (1.10) з (1.3), бачимо надзвичайне спрощення моделі. Якщо раніше нам треба було оцінювати параметр αλ та нескінченну кількість параметрів βі, тепер достатньо оцінити лише три змінних: α,βо і λ, тобто немає причин очікувати мультиколінеарність. Фактично ми позбулись мультиколінеарності заміною хt-1, хt-2 … на одну змінну, тобто уt-1.
. Ця процедура відома як перетворення Койка. Порівнюючи (1.10) з (1.3), бачимо надзвичайне спрощення моделі. Якщо раніше нам треба було оцінювати параметр αλ та нескінченну кількість параметрів βі, тепер достатньо оцінити лише три змінних: α,βо і λ, тобто немає причин очікувати мультиколінеарність. Фактично ми позбулись мультиколінеарності заміною хt-1, хt-2 … на одну змінну, тобто уt-1.
 .
.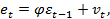
 ), знаходять оцінку
), знаходять оцінку 
 ,
,
 параметрів
параметрів  коефіцієнта автокореляції ρ не стане меншою від наперед заданого числа (величини заданої похибки).
коефіцієнта автокореляції ρ не стане меншою від наперед заданого числа (величини заданої похибки). , за допомогою якого перевіряють мультиколінеарність усього масиву факторних ознак; — F -критерій, за його допомогою перевіряють гіпотезу Н0: коефіцієнт детермінації
, за допомогою якого перевіряють мультиколінеарність усього масиву факторних ознак; — F -критерій, за його допомогою перевіряють гіпотезу Н0: коефіцієнт детермінації  дорівнює нулю:
дорівнює нулю:  та гіпотезу H1:коефіцієнт детермінації
та гіпотезу H1:коефіцієнт детермінації  не дорівнює нулю:
не дорівнює нулю: 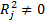 . За допомогою F- тесту перевіряють кореляцію кожної факторної ознаки з усіма іншими; — Т -критерій, на підставі якого перевіряють гіпотезу Н0: частковий коефіцієнт кореляції дорівнює нулю:
. За допомогою F- тесту перевіряють кореляцію кожної факторної ознаки з усіма іншими; — Т -критерій, на підставі якого перевіряють гіпотезу Н0: частковий коефіцієнт кореляції дорівнює нулю: 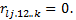 та гіпотезу Н1: частковий коефіцієнт кореляції не дорівнює нулю:
та гіпотезу Н1: частковий коефіцієнт кореляції не дорівнює нулю:  де
де  — часткові коефіцієнти кореляції, які характеризують тісноту зв'язку між факторними ознаками хl та хj за умови, що решта факторних ознак не впливає на цей зв'язок. За допомогою t- тесту перевіряють наявність лінійної кореляційної залежності кожної пари факторних ознак. Порівняння розрахованих значень цих критеріїв з їхніми критичними значеннями дає можливість зробити висновки щодо наявності чи відсутності мультиколінеарності.
— часткові коефіцієнти кореляції, які характеризують тісноту зв'язку між факторними ознаками хl та хj за умови, що решта факторних ознак не впливає на цей зв'язок. За допомогою t- тесту перевіряють наявність лінійної кореляційної залежності кожної пари факторних ознак. Порівняння розрахованих значень цих критеріїв з їхніми критичними значеннями дає можливість зробити висновки щодо наявності чи відсутності мультиколінеарності. , (7.78) де п — величина вибірки для кожної змінної (i=1,n); k- кількість факторних ознак у моделі (j=1,k);
, (7.78) де п — величина вибірки для кожної змінної (i=1,n); k- кількість факторних ознак у моделі (j=1,k);  — середнє значення j- ї факторної ознаки;
— середнє значення j- ї факторної ознаки;  — дисперсія j -ї факторної ознаки.
— дисперсія j -ї факторної ознаки. Крок 2. Обчислення кореляційної матриці
Крок 2. Обчислення кореляційної матриці  де X* — матриця нормалізованих значень факторних ознак.
де X* — матриця нормалізованих значень факторних ознак. матриці R є парні коефіцієнти кореляції, які характеризують тісноту зв'язку між l-ю та j-ю факторними ознаками. Однак на підставі знайденої кореляційної матриці В не можна стверджувати, що отриманий зв'язок є явищем мультиколінеарності. Крок 3. Обчислення значення
матриці R є парні коефіцієнти кореляції, які характеризують тісноту зв'язку між l-ю та j-ю факторними ознаками. Однак на підставі знайденої кореляційної матриці В не можна стверджувати, що отриманий зв'язок є явищем мультиколінеарності. Крок 3. Обчислення значення  -критерію —
-критерію — 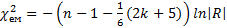 , де
, де  — визначник кореляційної матриці R. Знаходимо табличне значення
— визначник кореляційної матриці R. Знаходимо табличне значення  при —
при —  ступенях вільності і рівні значущості α. Якщо
ступенях вільності і рівні значущості α. Якщо 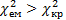 , тоімовірністю р=1-α можна стверджувати, що в масиві факторних ознак є мультиколінеарність. Якщо
, тоімовірністю р=1-α можна стверджувати, що в масиві факторних ознак є мультиколінеарність. Якщо  , то з імовірністю р=1-α можемо зробити висновок щодо відсутності мультиколінеарності. Крок 4. Визначення матриці помилок С=
, то з імовірністю р=1-α можемо зробити висновок щодо відсутності мультиколінеарності. Крок 4. Визначення матриці помилок С=  . Крок 5. Розрахунок значень F- критерію —
. Крок 5. Розрахунок значень F- критерію —  де
де  -діагональні елементи матриці С. При заданих ступенях вільності n-k і k-1 та рівні значущості α знаходимо табличне значення критерію і порівнюємо розраховані значення
-діагональні елементи матриці С. При заданих ступенях вільності n-k і k-1 та рівні значущості α знаходимо табличне значення критерію і порівнюємо розраховані значення  з табличним
з табличним  . Якщо
. Якщо 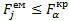 , то з імовірністю р=1-α гіпотезу Н0 приймаємо, тобто факторна ознака хj не є колінеарною з усіма іншими. На підставі діагональних елементів матриці С можна розрахувати коефіцієнти детермінації для кожної факторної ознаки:
, то з імовірністю р=1-α гіпотезу Н0 приймаємо, тобто факторна ознака хj не є колінеарною з усіма іншими. На підставі діагональних елементів матриці С можна розрахувати коефіцієнти детермінації для кожної факторної ознаки: 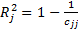 . Коефіцієнт детермінації
. Коефіцієнт детермінації 
 — елемент матриці С, який розміщений на перетині l-ї стрічки та j- го стовпця;
— елемент матриці С, який розміщений на перетині l-ї стрічки та j- го стовпця;  діагональні елементи матриці С.
діагональні елементи матриці С.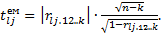 Розраховані значення критерію
Розраховані значення критерію 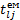 порівнюємо з табличним значенням
порівнюємо з табличним значенням  при n-k ступенях вільності і рівні значущості α. Якщо
при n-k ступенях вільності і рівні значущості α. Якщо  то з імовірністю р=1-α гіпотезу Н0 відкидаємо, тобто між факторними ознаками x l і хj наявна колінеарність. Якщо
то з імовірністю р=1-α гіпотезу Н0 відкидаємо, тобто між факторними ознаками x l і хj наявна колінеарність. Якщо 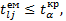 то з імовірністю р=1-α гіпотезу Н0 приймаємо, тобто факторні ознаки хl і хj неколінеарні.
то з імовірністю р=1-α гіпотезу Н0 приймаємо, тобто факторні ознаки хl і хj неколінеарні.
 де Ỹ- n-вимірна матриця-стовпець теоретичних значень результуючої змінної, що розраховані на підставі кореляційно-регресійної моделі; b – (k+1) – вимірна матриця-стовпець оцінок параметрів кореляційно-регресійної моделі.
де Ỹ- n-вимірна матриця-стовпець теоретичних значень результуючої змінної, що розраховані на підставі кореляційно-регресійної моделі; b – (k+1) – вимірна матриця-стовпець оцінок параметрів кореляційно-регресійної моделі.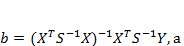 стандартну похибку — згідно
стандартну похибку — згідно  . Отже, ми можемо побудувати довірчі інтервали та критерії перевіряння статистичної значущості параметрів регресії β.
. Отже, ми можемо побудувати довірчі інтервали та критерії перевіряння статистичної значущості параметрів регресії β.


