Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перевірка гіпотез про рівність дисперсій двох незалежних нормально розподілених випадкових величин.Содержание книги
Поиск на нашем сайте
Нехай дві генеральні сукупності характеризуються відповідно дво-;залежними нормально розподіленими випадковими величинами X і Y із невідомими дисперсіями Dr(Х) і Dr(Y) відповідно. Допускається, що: • відомі вибірки обсягу п генеральної X та обсягу т генеральної Y; • івень значущості Правило 1. Якщо H 0: Dr(Х) = Dr(Y), а H 0: Dr(Х) > Dr(Y), то перевірка гіпотез здійснюється за правилом: 1. Обчислюється хв і ув. 2. Обчислюються виправлені вибіркові дисперсії DХв і DYв. 3. Обчислюється емпіричне значення критерію за формулою
4. За таблицею критичних точок розподілу Фішера - Снедекора для заданого рівня значущості 5. Робиться висновок:
Правило 2. Якщо H 0: Dr(Х) = Dr(Y), а H 0: Dr(Х) критична точка Відмінність між функціональною, статистичною та кореляційною залежностями. Дві випадкові величини X і У можуть бути або залежними одна від другої, або бути незалежними. Якщо ці величини залежні між собою, то ця залежність може бути або функціональною, або статистичною. Строга функціональна залежність на практиці трапляється рідко, частіше - статистична. Статистичною залежністю між двома величинами називають таку залежність, за якої зміна розподілу ймовірностей однієї з них викликає зміну розподілу ймовірностей другої. Якщо за статистичної залежності двох величин за зміни однієї з них змінюється середнє значення іншої, то таку статистичну залежність називають кореляційною. У багатьох практичних задачах часто виникає потреба - на основі вибірки встановити й оцінити залежність однієї випадкової величини від іншої (чи інших), встановити взаємозв'язок між цими величинами. Такі задачі розв'язуються за допомогою кореляційного та регресійного аналізів. Вибірковий коефіцієнт кореляції двовимірної випадкової величини (X, Y) і визначення за його допомогою лінійного зв'язку між складовими X і Y. Нехай двовимірна випадкова величина (X, У) розподілена нормально і нехай за заданим рівнем значущості Перевірка гіпотези здійснюється за правилом: 1. Обчислюється хвіув. 2. Обчислюється середні квадратичні відхилення σвх і σву. 3. Обчислюється rв 4. Обчислюється емпіричне значення критерію Стьюдента за формуллою 5. За таблицею критичних точок Стьюдента за даними 6. Робиться висновок
Рівняння лінійної регресії та його знаходження методом найменших квадратів. Регресійний аналіз встановлює аналітичну форму залежності. Математична модель регресії, або просто – регресійна модель, -це аналітичний вираз залежності Y від Х. Базою регресійних моделей служать вибіркові рівняння регресії, які записуються у формі: Вибіркового рівняння регресії У на Х Або вибіркового рівняння регресії Х на У Основним методом для знаходження наближених значень таких параметрів є метод найменших квадратів. Його ідея полягає в тому щоб знайти такі точкові оцінки a* і b* параметрів a і b, для яких пряма Y*x= a*x+ b* Була б найближчою до точок (x1, у1), … (xn, уn) За міру відхилення шуканої прямої від точок (xi, уi) вибирають величину За точкові оцінки a* і b* параметрів a і b вибирають мінімальне значення квадрату відхилення тобто S(a*,b*)=min S(a,b) Метод знаходження таких оцінок параметрів a і b з використання попередньої функції називається методом найменших квадратів. Рівняння лінійної регресії Yx= a вx+ bв Коефіцієнт a в називається коефіцієнтом регресії. Вираження рівняння лінійної регресії через коефіцієнт кореляції. Лнійне рівняння регресії можна подати й через коефіцієнт кореляції як формулу
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 343; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.3.17 (0.006 с.) |

 .
.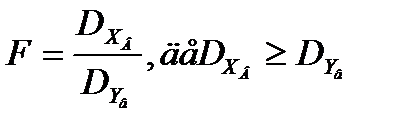
 і ступенів вільності k1=п -1 і k2 = т -1 знаходимо критичну точку правосторонньої критичної області fп.кр =
і ступенів вільності k1=п -1 і k2 = т -1 знаходимо критичну точку правосторонньої критичної області fп.кр =  .
.

 Dr(Y), то перевірка гіпотез здійснюється за вищенаведеним правилом, у якому змінюється лише методика обчислення критичних точок. У такому разі
Dr(Y), то перевірка гіпотез здійснюється за вищенаведеним правилом, у якому змінюється лише методика обчислення критичних точок. У такому разі
 є двосторонньою
є двосторонньою треба перевірити гіпотезу H0: rху = 0 при Н1:r ху
треба перевірити гіпотезу H0: rху = 0 при Н1:r ху  0.
0.
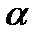 , зосередженому у верхньому рядку табліщі, і числом ступені k=n-2 знаходять критичну точку
, зосередженому у верхньому рядку табліщі, і числом ступені k=n-2 знаходять критичну точку  двосторонньої критичної області.
двосторонньої критичної області.