Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтегральна теорема Лапласа.Содержание книги
Поиск на нашем сайте
Якщо у схемі Бернуллі и є досить великим, то ймовірність появи події А не менша ніж м1 і не більша ніж м2 разів наближено може бути знайдена за формулою:
13. Формула Пуассона для обчислення ймовірностей в схемі незалежних випробувань Бернуллі та умови застосування. Формула Пуаcсона. Якщо в кожному з n незалежних повторних випробувань, а n велике, то Найімовірніше число появи події у послідовності випробувань за схемою Бернуллі та метод його обчислення. Найімовірнішим числом m0 появи події А в n незалежних випробовуваннях називається число, для якого ймовірність не менша ймовірності кожного з решти можливих варіантів, тобто З нерівності (1) отримується:
Імовірність відхилення відносної частоти події від її ймовірності. Відхилення відносної частоти від імовірності. Імовірність того, що при проведенні n незалежних випробувань відхилення відносної частоти події А від її ймовірності за модулем не перевищить e, визначається за формулою:
Дискретна випадкова величина та закон розподілу її ймовірностей. Дискретною випадковою величиною називають таку випадкову величину, яка може приймати відокремлені ізольовані одне від одного числові значення. Дискретні випадкові величини використовуються для опису та аналізу випадкових явищ і процесів у природознавстві, економіці і т.д. Нехай дискретна випадкова величина Х набуває значень х1, х2,….,хn з відповідними ймовірностями р1, р2,…, рn. Законом розподілу дискретної випадкової величини називається вказана відповідність між усіма її можливими значеннями та їх імовірностями. Оскільки в одному випробуванні події Х=х1, Х=х2, …. Х=хn утворюють повну групу, то р1 + р2 +…..+ рn = 1 Законом розподілу дискретної випадкової величини записують таблично, графічно чи аналітично. Біномінальний закон розподілу ймовірностей дискретної випадкової величини. Якщо умови відповідають схемі Бернуллі і розподіл імовірностей визначається за формулою Бернуллі, то такий розподіл називається біномним. Аналітичний запис закону має вигляд P(X = m) = Розподіл Пуассона ймовірностей дискретної випадкової величини. Якщо у схемі Бернуллі досить великими є n a p чи q близькі до нуля і розподіл імовірностей визначається формулою Пуассона, то такий розподіл називається розподілом Пуассона. Аналітичний запис закону має вигляд P (X = m) =
Математичне сподівання дискретної випадкової величини, його ймовірнісний зміст та властивості. Математичне сподівання M(X) дискретної випадкової величини X називається сума добутків усіх можливих її значень на їх імовірності, тобто M(X) = Якщо множина значень дискретної випадкової величини Х є нескінченна і зліченна, то M(X) = причому математичне сподівання існує, якщо ряд справа у останній рівності збіжний абсолютно. Математичне сподівання має такі основні властивості: 1. M(С) = С (С – стала величина) 2. M(СХ) = С × M(X) 3. М ( 4. М ( 5. M(X - M(X)) = 0 Імовірнісний зміст математичного сподівання: математичне сподівання випадкової величини X наближено дорівнює середньому арифметичному зваженому її спостережуваних значень. Дисперсія і середнє квадратичне відхилення дискретної випадкової величини та їх ймовірнісний зміст. Основні властивості дисперсії. Дисперсією D(X), дискретної випадкової величини Х називається математичне сподівання квадрата відхилення цієї величини від її математичного сподівання, тобто D(X) = Використавши властивості математичного сподівання, формулу можна звести до вигляду: D(X) = М ( У випадку, коли множина різних значень дискретної випадкової величини Х є нескінченна і зліченна, то D(X) = D(X) = за умови, що числові ряди в правих частинах цих формул є збіжні. Дисперсія має такі основні властивості: 1. D(X)≥0 2. D(С) = 0 3. D(СX) = 4. D ( 5. D ( Cереднім квадратичним відхиленням ДВВ Х називають корінь квадратний з дисперсії D(X) і позначають σ(Х), тобто σ(Х) =
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.10.139 (0.009 с.) |

 , де
, де  ,
, 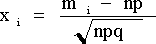 , а
, а  .
.
 ..Якщо найімовірніше число, то повинні виконуватись такі умови:
..Якщо найімовірніше число, то повинні виконуватись такі умови:  (1),
(1),  (2)
(2) звідки (після скорочень):
звідки (після скорочень):  .
.
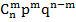 (m = 0,1,2,…,n).
(m = 0,1,2,…,n). 
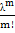
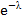 , де λ = np /Цей закон можна записати у формі таблиці:
, де λ = np /Цей закон можна записати у формі таблиці:

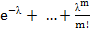
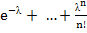
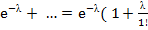
 =1
=1

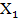 ±
±  ± … ±
± … ± 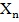 ) = М (
) = М ( ) ± … ±
) ± … ±  )
) =
=  M(X)
M(X) 

 ) – [M (X)
) – [M (X)  =
=  – [M (X)
– [M (X)  - M (X)
- M (X)  або
або – [M (X)
– [M (X)  × D(X)
× D(X) ) (для незалежних
) (для незалежних  + (М (
+ (М (