
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числові характеристики середнього арифметичного однаково розподілених взаємно незалежних дискретних випадкових величин та їх практичне значення.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Чисельні характеристики (математичне сподівання, дисперсія, середнє квадратичне відхилення) середнього арифметичного M ( Значення середнього арифметичного результатів вимірювань ознаки випадкової величини є надійнішим і ближчим до істинної характеристики цієї ознаки, ніж окремий результат. Функція розподілу випадкової величини та її графік. Функцією розподілу (інтегральною функцією розподілу, інтегральним законом розподілу) випадкової величини Х називається ймовірність того, що в результаті випробування вона набуде значення, меншого за х, тобто F (X) = P (X < x)
Формула для обчислення ймовірності попадання значень випадкової величини Х в заданий інтервал, яка виражається через функцію розподілу. Ймовірність того, що випадкова величина Х набуде значення з проміжку [a; b), дорівнює приросту функції розподілу на цьому проміжку, тобто Р (а ≤ Х < b) = F (b) – F (a) Густина розподілу неперервної випадкової величини та її графік. Густиною розподілу неперервної випадкової величини Х називається функція f(x), яка дорівнює першій похідній від функції розподілу F (x), тобто f(x) =
Формула для обчислення ймовірності попадання значень випадкової величини в заданий інтервал, яка виражається через густину розподілу. Ймовірність того, що неперервна випадкова величина Х набуде значення з інтервалу (а; b), дорівнює невизначеному інтегралу від густини її розподілу в межах від а до b, тобто:Р (а < Х < b) = Математичне сподівання неперервної випадкової величини. Математичне сподівання неперервної випадкової величини Х називають число М(Х), яке визначається рівністю:M(X) = якщо можливі значення НВВ Х належать інтервалу (а; b), абоM(X) =
Дисперсія і середнє квадратичне відхилення неперервної випадкової величини. Дисперсією неперервної випадкової величини Х називають математичне сподівання квадрата її відхилення Х – М(Х), тобто: D(X) = Для обчислення дисперсії неперервної випадкової величини часто використовують більш зручні формули: D(X) = Середнє квадратичне відхилення σ(Х) неперервної випадкової величини Х визначається рівністю: σ(Х) = Числові характеристики рівномірно розподіленої випадкової величини. Математичне сподівання М(Х) = Дисперсія D(X) = Середнє квадратичне відхилення σ(Х) = Нормальний закон розподілу ймовірностей неперервної випадкової величини та ймовірностей зміни параметрів розподілу. НВВ Х називається розподіленою за нормальним законом (або нормально-розподіленою) з параметрами -∞<а<∞ і Ϭ>0, якщо густина розподілу ймовірностей має вигляд
Формула для обчислення імовірності попадання значень нормально розподіленої випадкової величини в заданий інтервал.
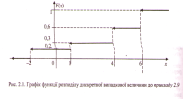
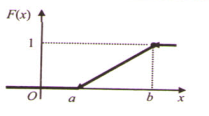
Рівномірний закон розподілу ймовірностей випадкової величини та графіки її густини й функції розподілу. НВВ Х називається рівномірно розподіленою на проміжку [a;b], якщо її густина f (x) на цьому проміжку є сталою величиною С. Стала С не є довільною. Оскільки
Числові характеристики показниково розподіленої випадкової величини. Математичне сподівання Формула для обчислення ймовірності попадання значень показникові розподіленої випадкової величини в заданий інтервал. Імовірність того, що показникові розподілена випадкова величина Ч набуде значень з проміжку (x1;x2) –
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 575; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 n взаємно незалежних і однаково розподілених дискретних випадкових величин
n взаємно незалежних і однаково розподілених дискретних випадкових величин 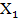 ,
,  , …,
, …, 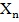 виражаються такими рівняннями:
виражаються такими рівняннями: , σ
, σ 

 (x)
(x)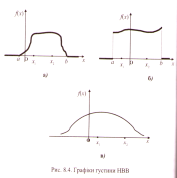
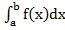
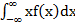 , якщо можливі значення НВВ Х належать усій осі Ox.У другому випадку припускається, що останній інтеграл збігається абсолютно, тобто існує
, якщо можливі значення НВВ Х належать усій осі Ox.У другому випадку припускається, що останній інтеграл збігається абсолютно, тобто існує Математичне сподівання неперервної випадкової величини є точки числової осі, яка характеризує її «середнє» значення або центр розподілу її значень.
Математичне сподівання неперервної випадкової величини є точки числової осі, яка характеризує її «середнє» значення або центр розподілу її значень.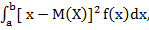 якщо можливі значення величини Х зосереджені на інтервалі (а; b), і D(X) =
якщо можливі значення величини Х зосереджені на інтервалі (а; b), і D(X) = 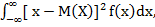 якщо можливі значення величини Х містяться на всій осі Ox.
якщо можливі значення величини Х містяться на всій осі Ox. D(X) =
D(X) = 
 Дисперсія і середнє квадратичне відхилення неперервної випадкової величини характеризують «розсіювання» можливих її значень в околі точки осі Ох, яка зображає математичне сподівання.
Дисперсія і середнє квадратичне відхилення неперервної випадкової величини характеризують «розсіювання» можливих її значень в околі точки осі Ох, яка зображає математичне сподівання.



 , де a, b – межі інтервалу.
, де a, b – межі інтервалу. , то С =
, то С =  f(x) =
f(x) =  F(x)=
F(x)= 

 Середнє квадратичне відхилення Ϭ(X)=
Середнє квадратичне відхилення Ϭ(X)=  Дисперсія D(X)=
Дисперсія D(X)= 




