
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точкова оцінка математичного сподівання нормально розподіленої випадкової величини.Содержание книги
Поиск на нашем сайте
За точкову оцінку М* математичного сподівання а=М(Х) генеральної сукупності вибирають вибіркове середнє тобто 44. Поняття точкової оцінки параметра розподілу випадкової величини та її незміщеність, змістовність і ефективність. Зв'язок точкових оцінок параметрів розподілу випадкової величини з її числовими характеристиками. Точкова оцінка параметра – це статистична оцінка невідомого параметра генеральної сукупності одним числом. 1)Оцінка 2)Оцінка 3) при розгляді великих за обсягом вибірок додається ще вимога змістовності. Оцінку 𝛩* називається змістовною, якщо при n→∞ вона прямує за ймовірністю до оцінюваного параметра 𝛩, тоюто виконується рівність Якщо при n→∞ дисперсія незміщеної точкової оцінки прямує до нуля, то така оцінка є також змістовною. За точкову оцінку M* математичного сподівання a=M(X) генеральної сукупності вибирають вибіркове середнє. За точкову оцінку D* дисперсії D(X) генеральної сукупності вибирають зміщену точкову оцінку дисперсії або незміщену вибіркову дисперсію. Точкова оцінка 46. Точкова оцінка дисперсії і середнього квадратичного відхилення нормально розподіленої випадкової величини. За точкову оцінку Д* дисперсії Д(Х) генеральної сукупності вибирають зміщену точкову оцінку дисперсії D* = Dв = 47. Інтервальні оцінки математичного сподівання нормально розподіленої випадкової величини у випадках, коли середньоквадратичне відхилення σ відоме і не відоме. Інтервальною називають оцінку, як визначається двома числами - кінцями інтервалу. Інтервал (Θ* - δ; Θ* + δ)називається довірчим, якщо він покриває оцінюваний параметр Θ із заданою наперед імовірністю γ. Нехай середнє квадратичне відхилення σr — відоме. У такому вападку довірчий інтервал, що покриває математичне сподівання аr = М(Х) із заданою ймовірністю γ, обчислюється за формулою 48. Інтервальна оцінка середнього квадратичного відхилення нормально розподіленої випадкової величини. О скільки дисперсія і середнє квадратичне відхилення пов’язані співвідношенням 49. Задача про статистичну перевірку гіпотези і критерій узгодження. Статистичною називають гіпотезу про вигляд розподілу генеральної сукупності або про параметри відомих уже розподілів.Статистичні гіпотези поділяються на дві основні групи: · непараметричні гіпотези — це гіпотези про закони розподілу ймовірностей випадкової величини генеральної сукупності; · параметричні гіпотези — це гіпотези про значення параметрів законів розподілу ймовірностей випадкової величини генеральної сукупності. Сформульована гіпотеза, яка піддається перевірці, називається нульовою(основною). Гіпотеза, яка єсуперечить нільовій чи є протилежною до не називається альтернативною (конкуруючою).Оскільки перевірка основної гіпотези проводиться за даними вибірки статистичними методами, то цю перевірку називають статистичною.Імовірність допустити помилку першого роду називається рівнем значущості.Статистичним критерієм гіпотези (або просто критерієм) називають випадкову величину К, за допомогою якої перевіряється основна гіпотеза.Значення випадкової величини К, яке обчислене на основі певної вибірки, називається емпіричним (або спостережним) значення критерію гіпотези.Множина значень критерію К, за яких основна гіпотеза відхиляється, називається критичною областю (КО).Множина значень критерію К, за яких основна гіпотеза приймається, називається областю прийняття гіпотез (ОПГ).
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.140.232 (0.007 с.) |

 Статистична оцінка невідомого параметра генеральної сукупності одним числом називається точковою. Точковою оцінкою невідомого параметра Θ генеральної сукупності називають однозначно визначену функцію Θ* = Θ*(х1, х2,...хп) на основі вибірки, за допомогою якої знаходять наближене значення параметра Θ.За точкову оцінку М* математичного сподівання а=М* генеральної сукупності вибирають вибіркове середнє, тобто М*= хв =
Статистична оцінка невідомого параметра генеральної сукупності одним числом називається точковою. Точковою оцінкою невідомого параметра Θ генеральної сукупності називають однозначно визначену функцію Θ* = Θ*(х1, х2,...хп) на основі вибірки, за допомогою якої знаходять наближене значення параметра Θ.За точкову оцінку М* математичного сподівання а=М* генеральної сукупності вибирають вибіркове середнє, тобто М*= хв = 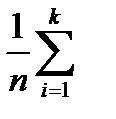 nixi
nixi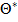 параметра
параметра 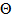 називається незміщеною, якщо за будь-якого обсягу вибірки її математичне сподівання дорівнює параметру, який оцінюється, тобто
називається незміщеною, якщо за будь-якого обсягу вибірки її математичне сподівання дорівнює параметру, який оцінюється, тобто  .В іншому випадку оцінка
.В іншому випадку оцінка 
 * середнього квадратичного відхилення обчислюється як середнє квадратичне відхилення
* середнього квадратичного відхилення обчислюється як середнє квадратичне відхилення 
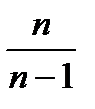 Dв =
Dв = 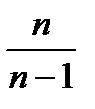
 Точкова оцінка σ* середнього квадратичного відхилення σ(Х) генеральної сукупності обчислюється за формулою σ * =
Точкова оцінка σ* середнього квадратичного відхилення σ(Х) генеральної сукупності обчислюється за формулою σ * = 
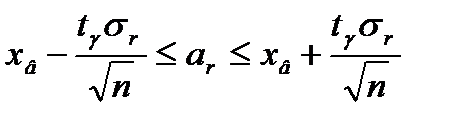 Де xв — вибіркове середнє; n – обсяг вибірки;
Де xв — вибіркове середнє; n – обсяг вибірки;  - значення аргументу функції Лапласа
- значення аргументу функції Лапласа 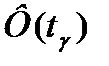 , за якого
, за якого  Величина
Величина  (точність оцінки)
(точність оцінки) , то досить оцінити
, то досить оцінити 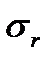 .Довірчий інтервал, який покриває σ із заданою надійністю γ, знаходимо за формулами:
.Довірчий інтервал, який покриває σ із заданою надійністю γ, знаходимо за формулами:  <
< 
 при
при 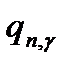 <1 або 0<
<1 або 0< 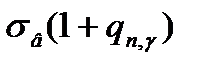 при
при 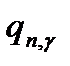 >1 Значення
>1 Значення 


