
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Чебишева та стійкість середнього арифметичного випадкових величин.Содержание книги
Поиск на нашем сайте
Теорема Чебишева: Нехай Х1, Х2, …, Хn- попарно незалежні випадкові величини, які мають скінченні математичні сподівання Показниковий розподіл імовірностей неперервної випадкової величини.Графік густини й функції розподілу. НВВ Х називається розподіленою за показниковим законом з параметром λ, якщо густина розподілу її ймовірностей має вигляд формули Графік густини:f(x)λ · x
Графік функції розподілу: F(x) 1 ………………………………..
O x
Теорема Бернуллі і стійкість відносних частот. Якщо в кожному з n незалежних повторних випробуваннях імовірність появи події A є однаковою і дорівнює p, то за досить великого n має місце рівність Центральна гранична теорема і її граничне значення. Теорема: Нехай випадкові величини Х1, Х2,…Хn, - незалежні і однаково розподілені, причому Система двох випадкових величин, її закон розподілу та числові характеристики складових. Розгляд двох чи більше випадкових величин в їх взаємозалежності розуміється як система випадкових величин. Така система ще має назву багатовимірної випадкової величини. Законом розподілу ймовірностей ДДВВ (X,Y) називається перелік її можливих значень ( Числові характеристики її складових знаходяться як для одновимірної ДВВ.
Кореляційний момент і коефіцієнт кореляції. Кореляційний момент Для обчислення кореляційного моменту ДДВВ користуються формулою Якщо випадкові величини X I Y – незалежні то Коефіцієнт кореляції це величина яка характеризує лише ступінь лінійної залежності між випадковими величинами X I Y. Умовні закони розподілу системи двох дискретних випадкових величин та їх числові характеристики. Умовним законом розподілу ДВВ Х за фіксованого значення Y= Математичні сподівання: Умовні дисперсії Умовні середні квадратичні відхилення Статистичний розподіл вибірки та його числові характеристики. Дискретним статистичним розподілом вибірки називається перелік витрат Розмах вибірки – це різниця між найбільшим і найменшим значеннями іі варіантами. Вибіркова дисперсія
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 198; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.43 (0.006 с.) |

 та обмежені в сукупності дисперсії
та обмежені в сукупності дисперсії  (обмежені одним і тим самим числом С, тобто
(обмежені одним і тим самим числом С, тобто  для усіх i=1,2,…,n, і нехай (у позначеннях)
для усіх i=1,2,…,n, і нехай (у позначеннях)  ,
,  . Тоді
. Тоді 
 тобто практично з достовірністю можна стверджувати, що різниця між середнім арифметичним випадкових величин і середнім арифметичним їх математичнх сподівань є як завгодно малою, якщо n – число випадкових величин є досить великим. Середнє арифметичне великого числа незалежних випадкових величин втрачає випадковий характер і має властивість стійкості.
тобто практично з достовірністю можна стверджувати, що різниця між середнім арифметичним випадкових величин і середнім арифметичним їх математичнх сподівань є як завгодно малою, якщо n – число випадкових величин є досить великим. Середнє арифметичне великого числа незалежних випадкових величин втрачає випадковий характер і має властивість стійкості.
 , де
, де  відносна частота появи події А, m – число появ події A, n – число випробувань,
відносна частота появи події А, m – число появ події A, n – число випробувань,  - будь-яке як завгодно мале число. Теорема Бернуллі стверджує, що відносна частота
- будь-яке як завгодно мале число. Теорема Бернуллі стверджує, що відносна частота  події А за досить великого числа випробувань є стійкою величиною.
події А за досить великого числа випробувань є стійкою величиною. ?
?  , i=1,2,…n. Розглянемо випадкову величину
, i=1,2,…n. Розглянемо випадкову величину  , для якої
, для якої  Тоді закон розподілу суми
Тоді закон розподілу суми  за
за  наближається до нормального з математичним сподіванням
наближається до нормального з математичним сподіванням  і середнім квадратичним відхиленням
і середнім квадратичним відхиленням  , тобто
, тобто 
 та відповідних ймовірностей p(
та відповідних ймовірностей p( спільної їх появи.
спільної їх появи. випадкових величин (X,Y) називається математичне сподівання добутку відхилен цих величин, тобто
випадкових величин (X,Y) називається математичне сподівання добутку відхилен цих величин, тобто 
 або
або  .
. , якщо ж
, якщо ж  то величини X I Y є залежними.
то величини X I Y є залежними.
 називається перелік усіх можливих значень
називається перелік усіх можливих значень 
 величини Ч та відповідних їм умовних імовірностей
величини Ч та відповідних їм умовних імовірностей 



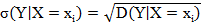
 і відповідних їм частот
і відповідних їм частот  чи відносних частот
чи відносних частот  Інтервальним статистичним розподілом вибірки називають відповідність між інтервалами варіаційного ряду та накопиченими частотами чи відносними накопиченими частотами. Числові характеристики: Вибірковим середнім
Інтервальним статистичним розподілом вибірки називають відповідність між інтервалами варіаційного ряду та накопиченими частотами чи відносними накопиченими частотами. Числові характеристики: Вибірковим середнім  статистичного розподілу вибірки називається середнє арифметичне значення її варіант
статистичного розподілу вибірки називається середнє арифметичне значення її варіант  з урахуванням їх частот
з урахуванням їх частот  .
. 

 (або
(або  статистичного розподілу вибірки – це вибіркова середня квадратів різниць між варіантами
статистичного розподілу вибірки – це вибіркова середня квадратів різниць між варіантами 
 або
або  Вибіркове середнє квадратичне відхилення:
Вибіркове середнє квадратичне відхилення:  Мода
Мода  дискретного статистичного розподілу вибірки називається те значення варіанти
дискретного статистичного розподілу вибірки називається те значення варіанти  дискретного статистичного розподілу вибірки називається значення середнього елемента варіаційного ряду.
дискретного статистичного розподілу вибірки називається значення середнього елемента варіаційного ряду.


