
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порівняння групових середніх за критерієм ФішераСодержание книги
Поиск на нашем сайте
У п. 3.1 говорилося про те, що в дисперсійному аналізі порівняння середніх здійснюється через порівняння дисперсій. Можна довести, що якщо гіпотеза про рівність групових середніх вірна (невірна), те вірна (невірна) і гіпотеза про рівність факторної й залишкової дисперсії. Справедливо й зворотне твердження: із правильності (хибності) гіпотези про дисперсії випливає правильність (хибність) гіпотези про середні. Будемо вважати, що ознака Для порівняння групових середніх нормально розподілених сукупностей з однаковими дисперсіями висувається нульова гіпотеза про рівність факторної й залишкової дисперсії при рівні значущості
Позначимо ступеня свободи чисельника й знаменника через Якщо Зауваження 1. Якщо виявиться, що Зауваження 2. Якщо спостережувані значення
де С приблизно дорівнює середньому значень чисел
При цьому факторна й залишкова дисперсія збільшаться в Зауваження 3. Якщо треба зрівняти середні попарно, то використовують критерій Стьюдента.
Приклад. Зроблено по 4 випробування на кожному із трьох рівнів. Результати випробувань наведені в таблиці 32. Методом дисперсійного аналізу при рівні значущості 0,05 перевірити нульову гіпотезу про рівність групових середніх. Передбачається, що вибірки витягнуті з нормальних сукупностей з однаковими дисперсіями. Таблиця 32
Розв’язання. Для спрощення обчислень із кожного спостережуваного значення віднімемо значення Таблиця 33
Користуючись таблицею і враховуючи, що число рівнів фактору
Знайдемо залишкову суму квадратів відхилень:
Знайдемо факторну й залишкову дисперсії:
Знайдемо спостережуване значення критерію Фішера:
З огляду на, що число ступенів свободи чисельника дорівнює Тому що
Питання й задачі для самоперевірки 1. Яка задача однофакторного дисперсійного аналізу? 2. Яка основна ідея дисперсійного аналізу? 3. Що відбивають загальна, факторна й залишкова суми квадратів відхилень? 4. На якій підставі в критерії Фішера порівняння середніх здійснюється через порівняння дисперсій?
Задача. Зроблено по чотири випробування на кожному із трьох рівнів фактору
Таблиця 34
Відповідь.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.35.247 (0.008 с.) |

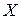 розподілена нормально. Вплив досліджуваного фактору може бути двояким: він може змінювати як істиний результат (середнє) спостережень, так і їхню дисперсію. Ми, однак, будемо припускати, що дисперсії хоча й невідомі, але постійні. Це припущення звичайно виправдується, якщо для спостережень використовуються ті самі прилади й та сама методика. Якщо ж стабільність дисперсії викликає сумнів, потрібно провести спеціальні дослідження за допомогою критеріїв Бартлета або Кохрана. У випадку значної зміни дисперсії в процесі спостережень потрібно спробувати її стабілізувати. Для цього є спеціальні математичні прийоми, на яких ми не будемо зупинятися.
розподілена нормально. Вплив досліджуваного фактору може бути двояким: він може змінювати як істиний результат (середнє) спостережень, так і їхню дисперсію. Ми, однак, будемо припускати, що дисперсії хоча й невідомі, але постійні. Це припущення звичайно виправдується, якщо для спостережень використовуються ті самі прилади й та сама методика. Якщо ж стабільність дисперсії викликає сумнів, потрібно провести спеціальні дослідження за допомогою критеріїв Бартлета або Кохрана. У випадку значної зміни дисперсії в процесі спостережень потрібно спробувати її стабілізувати. Для цього є спеціальні математичні прийоми, на яких ми не будемо зупинятися. . Потім обчислюють
. Потім обчислюють  - критерій Фішера:
- критерій Фішера: . (3.3.1)
. (3.3.1) і
і  відповідно й порівнюючи
відповідно й порівнюючи  зі знайденим по таблиці критичних точок розподілу Фішера (додаток 2) при даних
зі знайденим по таблиці критичних точок розподілу Фішера (додаток 2) при даних 
 , то нульову гіпотезу відкидаємо, тобто будемо вважати, що групові середні «у цілому» відрізняються значуще. Якщо
, то нульову гіпотезу відкидаємо, тобто будемо вважати, що групові середні «у цілому» відрізняються значуще. Якщо  , то немає підстав відкинути нульову гіпотезу. У цьому випадку вважають, що групові середні відрізняються незначуще.
, то немає підстав відкинути нульову гіпотезу. У цьому випадку вважають, що групові середні відрізняються незначуще. , то звідси вже випливає справедливість нульової гіпотези про рівність групових середніх.
, то звідси вже випливає справедливість нульової гіпотези про рівність групових середніх. - десяткові дроби зі
- десяткові дроби зі  знаками після коми, для полегшення обчислень краще перейти до цілих чисел
знаками після коми, для полегшення обчислень краще перейти до цілих чисел ,
, .
. раз, але їх відношення
раз, але їх відношення 





 . Тоді
. Тоді  . Складемо розрахункову таблицю 33
. Складемо розрахункову таблицю 33




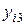







 , число випробувань на кожному рівні
, число випробувань на кожному рівні  , знайдемо загальну й факторну суми квадратів відхилень по формулах (3.2.1.7) і (3.2.1.8).
, знайдемо загальну й факторну суми квадратів відхилень по формулах (3.2.1.7) і (3.2.1.8). ;
; .
. .
. ;
; .
. .
. , а знаменника
, а знаменника  , при рівні значущості
, при рівні значущості  по таблиці знаходимо критичну точку
по таблиці знаходимо критичну точку  .
. . Методом дисперсійного аналізу при рівні значущості 0,05 перевірити нульову гіпотезу про рівність групових середніх. Передбачається, що вибірки витягнуті з нормальних сукупностей з однаковими дисперсіями. Результати випробувань наведені в таблиці 34
. Методом дисперсійного аналізу при рівні значущості 0,05 перевірити нульову гіпотезу про рівність групових середніх. Передбачається, що вибірки витягнуті з нормальних сукупностей з однаковими дисперсіями. Результати випробувань наведені в таблиці 34


 = 428;
= 428;  ;
;  ;
;  ;
;  ;
;  ;
;  . Групові середні «у цілому» різняться значуще.
. Групові середні «у цілому» різняться значуще.


