
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дві основні задачі теорії кореляціїСодержание книги
Поиск на нашем сайте
Перша задача теорії кореляції – установити вид функції регресії. Точне рівняння регресії (наприклад Після того, як рівняння регресії знайдене, його треба піддати статистичному аналізу. Регресійний аналіз дозволяє в багатьох випадках оцінити погрішність заміни істиної регресії наближеною, а також перевірити значущість всіх доданків знайденого рівняння регресії в порівнянні з випадковою помилкою спостережень. Вивчення регресійного аналізу в досить повному об'ємі не передбачено навчальною програмою. Друга задача теорії кореляції складається в оцінці тісноти (сили) кореляційних зв'язків за допомогою певних показників. Таке дослідження називається кореляційним аналізом.
Про вибір теоретичного виду рівняння регресії з урахуванням особливостей економіко - математичного Моделювання Складаючи рівняння регресії за статистичним даними, ми будуємо економіко - математичну модель досліджуваного явища, тому важливо знати загальні особливості економіко-математичного моделювання. Розглянемо загалом ці особливості. 1.Будь-яка реальна економічна система являє собою надзвичайно складну систему, що, як правило, містить дуже багато параметрів. Чим більше параметрів враховано в моделі, тим вона більш адекватно відображає економічну систему, що моделюється. Проте, прагнення врахувати якнайбільше параметрів може привести до істотного ускладнення математичного аналізу моделі. Часто цей аналіз зробити дуже важко або зовсім неможливо, тому будується кілька типів моделей, кожна з яких найбільше повно відображає певні сторони економічного процесу. При розв’язанні конкретної економічної задачі обирають ту модель, що найбільш адекватна реальності. 2. Економічна система, як правило, попадає під вплив цілого ряду зовнішніх і внутрішніх факторів, які важко або неможливо прогнозувати, а виходить, і врахувати в моделі. Такими факторами можуть бути недопоставка устаткування, зміна попиту на продукцію системи й т.п. (зовнішні впливи), велика аварія, зміни в технології і т. ін. (внутрішні впливи). Частина факторів не може фігурувати в моделі, тому що немає можливості оцінити їх кількісно. Наприклад, при прогнозуванні попиту важко кількісно оцінити міру впливу на попит моди, національних особливостей і т.п. Крім того, кількість факторів у моделі об'єктивно доводиться обмежувати через відсутність надійної економічної інформації. 3. Математична модель економічної системи, як правило, не дозволяє по початковому її стані визначити розвиток системи (відкрита модель). У моделі завжди присутні вільні функції й параметри, які обумовлюють у середньому можливість моделі впливати на процеси, що відбуваються в системі. 4. Математичні моделі економічних систем істотно залежать від прийнятих економічних концепцій. 5. Математична модель економічної системи, як і будь-яка математична модель реального об'єкта або процесу, повинна бути підтверджена практикою, експериментом. Експериментальна перевірка економіко – математичної моделі, як правило, пов'язана із цілим рядом суб'єктивних і об'єктивних труднощів. По-перше, експеримент може привести до зміни внутрішніх і зовнішніх умов функціонування економічної системи або її підсистеми; не кожний керівник захоче відмовитися від звичайних для нього управлінських рішень у тій або іншій ситуації. Крім того, люди, які приймають управлінські рішення, мають різну кваліфікацію, різні джерела інформації. У результаті всього цього реалізація математичної моделі на практиці в одному випадку може дати гарний ефект, а в іншому при аналогічних об'єктивних умовах привести до результатів, які далекі від прогнозованих. По-друге, економіко – математична модель містить у собі багато показників, кількісну оцінку яких дають офіційні статистичні установи. На жаль, така інформація не завжди надійна й не завжди оперативно надається. Це може привести до того, що навіть гарна модель при експерименті не підтвердиться. По-третє, експеримент, у якому беруть участь люди, завжди має свою специфіку. Сам факт відносини до експерименту вже впливає па процес, що вивчається, у зв'язку із чим завжди можливі необ'єктивні висновки. Використання економіко – математичних моделей вимагає творчого підходу до рішення управлінських задач, володіння мистецтвом керування. Керівник, що користується цими моделями, і математик, що моделює економічні процеси, повинні в певній мірі володіти й практичними й науковими аспектами проблеми. Математичне моделювання аж ніяк не претендує на роль єдиного методу дослідження економічних систем. Наприклад, у теорії й практиці прогнозування економічного розвитку застосовують також різні статистичні методи експертних оцінок. Ефективність наукового дослідження залежить від умілого сполучення різних методів. Велике значення має обмірковування ситуації на сугубо економічному рівні, кваліфіковане усвідомлення економічного процесу й результатів, які прогнозуються або вже отримані. Різні методики дослідження, як правило, взаємно доповнюють одна одну, вони перебувають у діалектичній єдності. Так, вдала математична модель може значно зменшити об'єм матеріалу, що вимагає статистичного аналізу, істотно поліпшує побудову експертних оцінок, У той же час сама структура математичної моделі може бути об'єктом аналізу, що здійснюється методом експертних оцінок, а необхідні параметри моделі можуть бути отримані статистичними методами. Математичні методи пізнання надзвичайно плодотворні, але ідеалізувати їх не можна; змістовні й формалізовані методи пізнання перебувають у діалектичній єдності. Недооцінка змістовних методів може привести до висновків, які далекі від реальності. Так, у свій час деякі економісти вважали, що всі проблеми реалізації деяких економічних законів можна звести до реалізації моделей математичного програмування, однієї з дисциплін прикладної математики. Розвиток методів математичного програмування привів до того, що з'явилася можливість будувати усе більше складні економіко – математичні моделі, одержувати усе більше загальні результати. Виникла ілюзія, що математика може дати ключ до аналізу не тільки окремих задач економіки, але й глобальних економічних процесів. Однак досить чіткі вихідні передумови первісних моделей, які відображали прості властивості конкретних економічних систем і могли бути вивчені експериментально, поступово замінялися більше загальними формальними передумовами, через що інформацію, що вважалася в моделі відомої, часто неможливо було одержати. У результаті цього численні моделі, що претендують на практичну реалізацію, по суті залишилися просто абстрактними побудовами. Треба мати на увазі, що без розвитку експериментальних і теоретичних досліджень у якій-небудь науці (наприклад, в економіці) неможливо істотне просування вперед за рахунок застосування тільки математичних методів. Для побудови змістовної математичної моделі в науці необхідне знання відповідних законів, необхідні, насамперед, змістовні наукові гіпотези. У теорії кореляції, мабуть, саме важке - це визначення теоретичної лінії зв'язку, що характеризує форму залежності ознак. Труднощі виникають із того, що потрібно знаходити наближену форму функціонального зв'язку, тоді як у реальності цей зв'язок лише в тім або іншому ступені наближається до функціонального. Але якщо залежність досить істотна, досить близько наближається до функціональноі, тоді саме теоретична лінія зв'язку і її параметри здобувають практичне значення; вони істотно допомагають у планових і економічних розрахунках, у багатьох інших сферах людської діяльності. В основі пошуків виду теоретичної лінії кореляційного зв'язку насамперед повинен лежати теоретичний якісний аналіз досліджуваного зв'язку. Якщо, наприклад, ми вивчаємо залежність відносного рівня витрат обігу від розміру товарообігу магазина, то міркуємо в такий спосіб. Витрати обігу складаються з різних видів витрат, які по-різному реагують на зміну розміру товарообігу торговельного підприємства. Із цього погляду всі витрати, що входять у витрати обіги, можна розділити на дві групи: умовно – постійні та умовно-змінні. Сталість або зміна тут розглядається відносно зміни сум витрат під впливом зміни товарообігу. Умовно-постійними будуть витрати на приміщення, оргтехніку, заробітну плату, виплачувану у вигляді твердих окладів, адміністративно-управлінські витрати й т.д. Суми цих витрат з ростом товарообігу або залишаються практично незмінними, або збільшуються значно повільніше, ніж росте товарообіг. Рівень їх (відсоток до товарообігу) у зв'язку із цим буде знижуватися. Умовно-змінними будуть транспортні витрати, витрати на ту частину заробітної плати, що виплачується у відсотку від обороту, і взагалі всі витрати, які утворюються у відсотку від обороту. Сума цих витрат буде зростати майже пропорційно росту товарообігу, а рівень їх у силу цього залишиться практично незмінним або буде знижуватися дуже незначно. З вищенаведеного аналізу випливає, що суму
де
Введемо товарообіг х (грн), помітивши, що
де коефіцієнт Тоді
Відносний рівень у витрат обігу дорівнює
тобто
Таким чином, економічний аналіз приводить нас у цьому випадку до рівняння регресії
Хоча це рівняння з'явилося в результаті економічного аналізу, воно, як і будь-яке інше рівняння регресії, після знаходження величин а й Лінійну регресію
варто очікувати в дуже багатьох дослідженнях, особливо там, де справедливий «закон рівномірного нагромадження». Наприклад, може бути відомо, що зміна величини У складних випадках, коли регресія явно буде нелінійною, вивчення лінійної регресії можна використовувати як перший етап дослідження, для того, щоб надалі внести в неї необхідні виправлення. При економічному аналізі статистичних даних треба звертати увагу на аномальні значення, що різко відрізняються від всієї сукупності даних. Такі значення можуть з'являтися в результаті грубої помилки в спостереженнях, звітах, розрахунках; у такому випадку їх необхідно проконтролювати й виправити. Аномальні значення можуть з'явитися також у результаті деяких особливих обставин («аварійна ситуація»), які варто врахувати окремо (наприклад, по частоті їхнього повторення), а із загальної сукупності виключити. На практиці, однак, не завжди вдається провести аналіз умов випробування. Найчастіше доводиться мати справа з остаточним цифровим матеріалом, у якому окремі дані викликають сумнів лише своїм значним відхиленням від інших. При цьому сама «значущість» відхилення багато в чому суб'єктивна - найчастіше доводиться зіштовхуватися з випадками, коли дослідник відкидає деякі спостереження як помилкові лише тому, що вони порушують уже створену їм в уяві картину досліджуваного процесу. Строгий науковий аналіз готового ряду спостережень може бути отриманий лише за допомогою математичної статистики. З курсу математичного аналізу відомо, що будь-яка функція, яку можна диференціювати ( При малих вибірках кожний зайвий зв'язок помітно зменшує точність наближеної регресії, тому тут бажано зменшити число невизначених коефіцієнтів, використовуючи інші функції. При цьому може виникнути регресія показникового, тригонометричного й іншого типів. Число коефіцієнтів у таких регрессиях найчастіше не перевищує двох-трьох, що дозволяє збільшити точність наближеної регресії. Якщо для підбора многочленної регресії існують спеціальні прийоми, то вибір типу інших регрессий складний. Добре, якщо вдається використовувати економічні, фізичні й інші міркування, аналогії; у противному випадку тип регресії можна визначити лише шляхом кропіткого підбора. Обчислення трансцендентної регресії в ряді випадків спрощується, якщо провести заміну змінних, перетворюючу таку регресію в лінійну. Наприклад, залежність показникового типу
перетворюється в лінійну логарифмуванням:
Щоб використовувати тут всі прийоми дослідження лінійної регресії, статистичні дані перераховуються по формулі
Аналогічно у випадку регресії виду
маємо
с подальшою заміною
Якщо теоретичні передумови досліджуваної залежності зовсім невідомі, однак логічно зв'язок між величинами повинен існувати, доводиться підбирати тип рівняння регресії лише по емпіричним даним. У цьому випадку попередній характер залежності можна з'ясувати, наносячи статистичні дані у вигляді точок на координатній площині. Нехай, наприклад, ці точки розташувалися так, як показано на рис.1.
Рис. 1
Загальну тенденцію залежності
Рис. 2 Виходячи з розташування точок, можна також вважати, що загальна тенденція зміни Ми вже відзначали, що залежність, що існує між явищами, повинна виражатися кількісно у відомій погодженості змін ознак, що зіставляються. Але потрібно мати на увазі, що наявність кореляції (та й усякого стохастичного зв'язку) не завжди свідчить про наявність дійсної, причинно-наслідкової залежності між величинами. Цей зв'язок може бути результатом простого співіснування явищ. Не виключено, що взявши, наприклад, статистичні дані про щомісячний продаж японських парасольок на Україні за якийсь рік і аналогічні дані про продаж пральних машин, ми формально виявимо між цими даними кореляційний зв'язок. Треба розуміти, що коли ми починаємо математичну обробку даних, то в силу абстрактності математики відволікаємося від конкретного смислу чисел. У статистичному ряді розподілу випадкової величини фігурують абстрактні числа й подальша їхня обробка ведеться на абстрактному рівні, на рівні формул. От чому, приступаючи до виявлення зв'язку між якимись величинами, треба насамперед усвідомити собі, чи можливий цей зв'язок з логічної сторони. Формальне застосування математичної статистики, не засноване на попередньому якісному вивченні зв'язків, може привести до абсолютно неправильних висновків. Кореляційний зв'язок може виникнути й у тому випадку, коли досліджувані явища, не будучи безпосередньо зв'язані один з одним, є наслідком однієї й тієї ж причини.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.78.184 (0.011 с.) |

 на Х) можна написати, якщо знати середні
на Х) можна написати, якщо знати середні 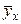 для всіх припустимих значеннях х. На практиці така ситуація, звичайно, неможлива. Більше того, навіть окремі значення
для всіх припустимих значеннях х. На практиці така ситуація, звичайно, неможлива. Більше того, навіть окремі значення  будемо вживати запис
будемо вживати запис 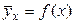 .
. витрат обігу можна представити у вигляді
витрат обігу можна представити у вигляді ,
, - постійні витрати,
- постійні витрати, - змінні витрати
- змінні витрати ,
, - змінні витрати на 1 грн. товарообігу.
- змінні витрати на 1 грн. товарообігу.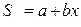 .
.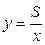 ,
,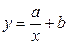 .
. .
.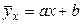
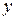 безпосередньо пов'язана зі зміною параметра х, але не залежить від того, яка «кількість» параметра х уже накопилася. Лінійна регресія має місце тоді, коли спостерігається тенденція рівномірного зростання або убування значень досліджуваної ознаки у зв'язку зі зміною ознаки-фактора.
безпосередньо пов'язана зі зміною параметра х, але не залежить від того, яка «кількість» параметра х уже накопилася. Лінійна регресія має місце тоді, коли спостерігається тенденція рівномірного зростання або убування значень досліджуваної ознаки у зв'язку зі зміною ознаки-фактора.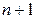 ) раз у точці
) раз у точці  й деякій її околиці, може бути з як завгодно великою точністю замінена многочленом (формула Маклорена). Тому, у принципі, будь-яке рівняння регресії можна шукати у вигляді многочлена
й деякій її околиці, може бути з як завгодно великою точністю замінена многочленом (формула Маклорена). Тому, у принципі, будь-яке рівняння регресії можна шукати у вигляді многочлена  , знаходячи його степінь шляхом послідовних підрахунків. Цей степінь, однак, може виявитися дуже високим, через що в рівнянні регресії буде дуже багато невизначених коефіцієнтів
, знаходячи його степінь шляхом послідовних підрахунків. Цей степінь, однак, може виявитися дуже високим, через що в рівнянні регресії буде дуже багато невизначених коефіцієнтів  . Ці коефіцієнти обчислюються по заданій вибірці й тому кожний з них являє собою деякий зв'язок, накладений на вибірку. Таким чином, многочлен степіня
. Ці коефіцієнти обчислюються по заданій вибірці й тому кожний з них являє собою деякий зв'язок, накладений на вибірку. Таким чином, многочлен степіня  накладає на вибірку (
накладає на вибірку (
 .
. .
.

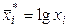 .
.
 від Х можна вважати лінійною (це показано на рис.1), але з таким же успіхом можна вважати, що
від Х можна вважати лінійною (це показано на рис.1), але з таким же успіхом можна вважати, що  (рис.2).
(рис.2).
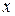 описується дугами парабол
описується дугами парабол  і багатьма іншими лініями. Тому що про реальний зв'язок досліджуваних величин у цьому випадку ми нічого не знаємо, то вибрати найбільш відповідний вид зв'язку допоможе лише кореляційний аналіз. Однак такий підбір може бути дуже трудомістким, тому що не виключено, що треба буде перебрати дуже велику кількість варіантів.
і багатьма іншими лініями. Тому що про реальний зв'язок досліджуваних величин у цьому випадку ми нічого не знаємо, то вибрати найбільш відповідний вид зв'язку допоможе лише кореляційний аналіз. Однак такий підбір може бути дуже трудомістким, тому що не виключено, що треба буде перебрати дуже велику кількість варіантів.


